Tomaschitz, R. (1995). Topologically induced chaos in the open universe, in: Dynamical Systems and Chaos (Tokyo, May 23-27, 1994, Y. Aizawa, S. Saito, K. Shiraiwa, eds.), World Scientific, Singapore, 1995, pp. 324-330.
Abstract (CDS, SAO/NASA ADS, Zbl 0989.83508)
An elementary account on chaos, its origins, and its physical impact in an infinite and multiply connected space-time is given. The anisotropy of the microwave background and the violation of the space-reflection symmetry (parity) by topological self-interference are reviewed in this context.
Zbl
0989.83508
Tomaschitz, Roman
Topologically induced chaos in the open universe
[A] Aizawa, Y. (ed.) et al., Dynamical systems and chaos. Vol. 2: Physics.
Proceedings of the international conference, Hachioji, Japan, May 23-27, 1994.
Singapore: World Scientific. 324-330 (1995). ISBN 981-02-2977-1
MSC 2000:
*83F05
Relativistic cosmology
37D45 Strange attractors, chaotic dynamics
|
Title: |
|
Topologically induced chaos in the open universe |
|
Authors: |
|
Tomaschitz, Roman |
|
Affiliation: |
|
AA(Department of Physics, Hiroshima University, Higashi-Hiroshima 739-8526, Japan) |
|
Publication: |
|
Dynamical Systems and Chaos (Y. Aizawa, S. Saito, K. Shiraiwa, eds.), World Scientific, Singapore, 1995, pp. 324-330. |
|
Publication Date: |
|
00/1995 |
|
Origin: |
|
AUTHOR |
|
Keywords: |
|
open Robertson-Walker cosmology, multiply connected hyperbolic 3-space, relativistic chaos |
|
Abstract Copyright: |
|
World Scientific |
|
Bibliographic Code: |
|
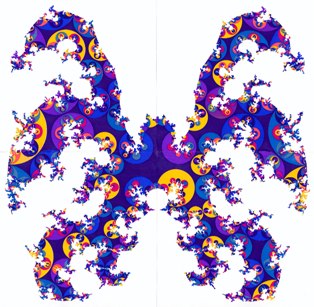
Fig. 2a full size image
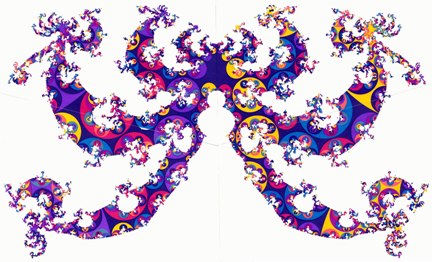
Fig. 2b full size image
Caption for Figs.
2a,b. The horizon at infinity of the Poincaré half-space H3. A
spacelike slice (F,Γ) is realized in H3 as a
polyhedron F with face-identification. The identifying transformations
generate a discrete group Γ which, applied to the polyhedron, gives a
tessellation Γ(F) of H3 with polyhedral images.
This tessellation induces by continuity also a tiling on the boundary of H3,
which is depicted here. The qualitative structure of the singular set depends
on the covering group Γ, for quasi-Fuchsian groups like here it is a
Jordan curve, for Schottky groups a Cantor set, cf. Refs. 7 and 8. The
spacelike slices can undergo global metrical deformations. The depicted tilings
correspond to 3-slices that are non-isometric, but have the same topology ((F,Γ)
~ I × S, S a Riemann surface, g(S) = 19, δ(Λ)
= 1.6) and curvature. These tilings make deformations as schematized in Fig. 1
quantitative. One can easily determine from them the chaotic or nearly chaotic
trajectories, which shadow each other over long times. Their lifts have initial
and end points in or close to the singular set, cf. Ref. 10. Projecting them
into the manifold, one obtains the chaotic nucleus.
description: Roman Tomaschitz (1995) Topologically induced chaos in the open universe, in: Dynamical Systems and Chaos (Y. Aizawa, S. Saito, K. Shiraiwa, eds.), World Scientific, Singapore, pp. 324-330.
Keywords: open Robertson–Walker cosmology, multiply connected hyperbolic 3-space, constant negative curvature, relativistic chaos, mixing and shadowing in the chaotic nucleus of the universe, galactic equidistribution, CP violation by topological self-interference, parity violation, temperature fluctuations in the cosmic microwave background radiation, particle creation by global metrical deformations of the open 3-space, topological evolution, topology change, cusp singularities, horospherical geodesic flow on open hyperbolic 3-manifolds, classical and quantum dispersion, Poincaré half-space, polyhedral tiling of hyperbolic space, fractal limit set of a Kleinian covering group, Hausdorff dimension, universal covering projection, chaotic world lines, quasi-Fuchsian groups, fibered hyperbolic 3-manifolds, compact Riemann surfaces
download full-text article (scanned PDF, 1.9 MB)