Tomaschitz, R. (1997). Chaos in the galactic dynamics, Fractals 5, 215-220, DOI: 10.1142/S0218348X97000206

 

 

Abstract (WorldSciNet, CDS, SAO/NASA ADS, Zbl 0906.58058)

An elementary survey of cosmic chaos, its origins, and its physical impact in an open and multiply connected universe is given. A new type of cosmic evolution by global metrical deformations, unpredicted by Einstein's equations, is pointed out. The uniformity and the inhomogeneities of the galactic background are discussed in this context. There is a finite region in the open 3-space in which the galactic world-lines are chaotic, and the mixing taking place in this chaotic nucleus of the universe provides a mechanism to create the galactic equidistribution.

  We review in a completely untechnical way how global metrical deformations of space-time cause particle creation in quantum fields, and induce angular fluctuations in the temperature of the cosmic microwave background radiation. They can generate topology changes without distorting the constant curvature of the 3-space. The micro-topology causes parity violation (i.e., a violation of the space-reflection symmetry) by self-interference.

 

 

Zbl 0906.58058
Tomaschitz, Roman
Chaos in the galactic dynamics
[J] Fractals 5, No.2, 215-220 (1997). ISSN 0218-348X

MSC 2000:

*58Z05 Appl. of global analysis to physics
83F05 Relativistic cosmology
83C47 Quantum field theory on curved space-times
83C75 Space-time singularities, etc.

Keywords: galactic dynamics; cosmic chaos

 

Title:

 

Chaos in the galactic dynamics.

Authors:

 

Tomaschitz, R.

Publication:

 

Fractals (Singapore), Vol. 5, No. 2, p. 215 - 220

Publication Date:

 

06/1997

Origin:

 

ARI

ARI Keywords:

 

Cosmology: Chaos, Universe: Galaxy Distribution, Cosmic Microwave Background: Temperature Fluctuations

Bibliographic Code:

 

1997Fract...5..215T

 

 

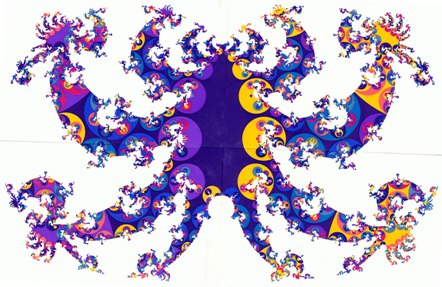
Fig. 1(a). The horizon at infinity of the Poincaré half-space H3, the universal covering space of the spacelike 3-sections of the extended RW cosmology. A spacelike slice (F,Γ) is realized in H3 as a polyhedron F with face-identification. The face-pairing transformations generate a discrete group Γ which gives, if applied to the polyhedron, a tessellation Γ(F) of H3 with polyhedral images. This tessellation induces by continuity also a tiling on the boundary of H3, which is depicted here (for three different slices), and which can easily be extended to three dimensions; the complete tiling of H3 is simply obtained by placing hemispheres onto the circular arcs. This polyhedral tiling of hyperbolic space H3 is the covering space construction for the RW geometry. So these two-dimensional tilings constitute a completely quantitative characterization of the three-dimensional spacelike slices.

Fig. 1(a) full size image

 

 

 

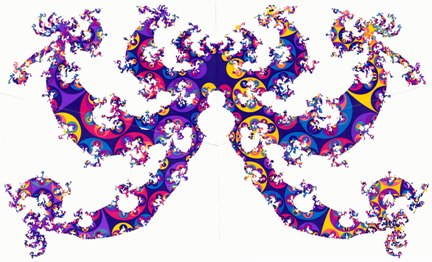
Fig. 1(b). The horizon at infinity of the Poincaré half-space H3, the universal covering space of the spacelike 3-sections of the extended RW cosmology. A spacelike slice (F,Γ) is realized in H3 as a polyhedron F with face-identification. The face-pairing transformations generate a discrete group Γ which gives, if applied to the polyhedron, a tessellation Γ(F) of H3 with polyhedral images. This tessellation induces by continuity also a tiling on the boundary of H3, which is depicted here (for three different slices), and which can easily be extended to three dimensions; the complete tiling of H3 is simply obtained by placing hemispheres onto the circular arcs. This polyhedral tiling of hyperbolic space H3 is the covering space construction for the RW geometry. So these two-dimensional tilings constitute a completely quantitative characterization of the three-dimensional spacelike slices.

Fig. 1(b) full size image

 

 

 

Fig. 1(c). The horizon at infinity of the Poincaré half-space H3, the universal covering space of the spacelike 3-sections of the extended RW cosmology. A spacelike slice (F,Γ) is realized in H3 as a polyhedron F with face-identification. The face-pairing transformations generate a discrete group Γ which gives, if applied to the polyhedron, a tessellation Γ(F) of H3 with polyhedral images. This tessellation induces by continuity also a tiling on the boundary of H3, which is depicted here (for three different slices), and which can easily be extended to three dimensions; the complete tiling of H3 is simply obtained by placing hemispheres onto the circular arcs. This polyhedral tiling of hyperbolic space H3 is the covering space construction for the RW geometry. So these two-dimensional tilings constitute a completely quantitative characterization of the three-dimensional spacelike slices.

Fig. 1(c) full size image

 

Fig. 1. (a)–(c) The horizon at infinity of the Poincaré half-space H3, the universal covering space of the spacelike 3-sections of the extended RW cosmology. A spacelike slice (F,Γ) is realized in H3 as a polyhedron F with face-identification. The face-pairing transformations generate a discrete group Γ which gives, if applied to the polyhedron, a tessellation Γ(F) of H3 with polyhedral images. This tessellation induces by continuity also a tiling on the boundary of H3, which is depicted here (for three different slices), and which can easily be extended to three dimensions; the complete tiling of H3 is simply obtained by placing hemispheres onto the circular arcs. This polyhedral tiling of hyperbolic space H3  is the covering space construction for the RW geometry. So these two-dimensional tilings constitute a completely quantitative characterization of the three-dimensional spacelike slices.

  The qualitative structure of the fractal limit set Λ(Γ) depends on the topology of the 3-slices, which is in turn determined by the covering group. For quasi-Fuchsian groups15 such as in this case, the limit set is a Jordan curve which is not self-similar. The 3-space fibers over an open interval, with Riemann surfaces (g = 49) as fibers. The colors label generations in the tiling procedure, the algorithm being given in Ref. 16. The tilings correspond to 3-slices which are non-isometric, but have the same topology and curvature. They are three snapshots in a time-parametrized sequence of continuous global deformations of the 3-space, realized here as deformations of the polyhedron F and the covering group Γ. The Hausdorff dimensions of the depicted limit sets vary only slightly, between 1.49 ± 0.03.

The chaotic trajectories have covering trajectories with initial and terminal points in Λ(Γ). If the end points are not in Λ(Γ) but close to it, then the trajectory is regular, but it is shadowed by chaotic trajectories over a long period.8 The convex hull of Λ(Γ) is the intersection of all hyperbolic half-spaces17 which contain Λ(Γ). Projected into (F,Γ) by means of the universal covering projection, it constitutes the chaotic center of the 3-space. Here again, the tilings on the boundary of H3 are the key to the explicit construction of this nucleus of the open 3-space by methods of elementary geometry.5,18

 

 

description: Roman Tomaschitz (1997) Chaos in the galactic dynamics, Fractals 5, 215.

 

Keywords: open Robertson–Walker cosmology, multiply connected hyperbolic 3-space, open hyperbolic 3-manifolds, constant negative curvature, chaoticity of galactic world lines, relativistic chaos, chaotic nucleus of the universe, galactic equidistribution, cosmic evolution by global metrical deformations, particle production in quantum fields, topology change, temperature anisotropy of the microwave background radiation, parity violation by self-interference, Poincaré half-space, universal covering space of the multiply connected 3-space, polyhedral tiling of hyperbolic space, fibered hyperbolic 3-manifolds, compact Riemann surfaces, fractal limit sets of Kleinian covering groups, quasi-Fuchsian groups, Hausdorff dimension, chaotic orbits, mixing and shadowing in the chaotic center of the open 3-space

 

download full-text article (scanned PDF, 2.7 MB)

 

back to index1989-99