Tomaschitz, R. (2025). Modeling heat-capacity data with multiparametric hazard functions, Applied Physics A 131, 353, DOI: 10.1007/s00339-025-08423-z
Abstract SpringerLink
Temperature-dependent cumulative hazard functions (CHFs) are used to analytically model empirical heat capacities of crystals and glasses, covering the entire temperature range from zero up to the melting point. The monotonically increasing and plateauing isochoric heat capacity curve, if normalized to one in the classical limit, is the cumulative distribution of a probability density f(T). The CHF H(T) is defined by the complementary cumulative distribution, being the negative logarithm thereof, and the molar isochoric heat capacity can be expressed as CV(T) = 3na/f R[1- exp(-H(T))], where na/f is the number of atoms per formula unit and R the gas constant. The data sets for the heat capacity are converted to data points of the CHF, which is represented as a multiply broken power-law density with amplitudes and exponents regressed from the data set. Specifically, the heat capacities of rutile, zinc, and vitreous SiO2 are discussed, which show substantial deviations from the Debye model of lattice vibrations in the intermediate temperature range. Residual plots and goodness-of-fit parameters are used to quantify the accuracy of the nonlinear least-squares regression of H(T). Index functions representing the Log-Log slope of the regressed heat capacities are studied and compared with their counterpart in the Debye theory. The empirical probability density f(T), proportional to the temperature derivative of the isochoric heat capacity, is obtained in closed form. Internal energy and entropy are found as expectation values over f(T), and their asymptotic expansions are derived by means of Hahn series and compared with the Debye model.
description: Roman Tomaschitz (2025) Modeling heat-capacity data with multiparametric hazard functions, Appl. Phys. A 131, 353.
Keywords: Molar isochoric heat capacity of solids; Cumulative hazard functions; Entropy; Internal energy; Rutile polymorph of TiO2; Titanium dioxide; Zinc; v-SiO2; Vitreous silica; Multiply broken power-law densities; Complementary cumulative distributions; Index functions; Hahn series; Multiparametric least-squares regression
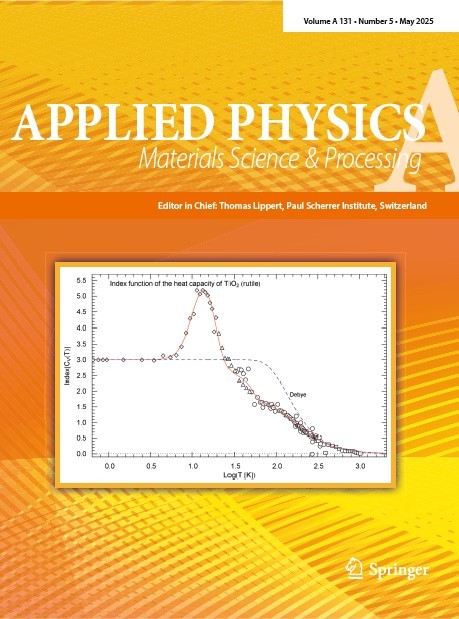
Cover image taken from DOI: 10.1007/s00339-025-08423-z
download full-text article (PDF) Full Text HTML