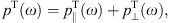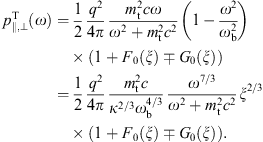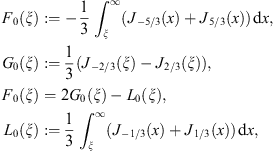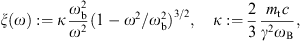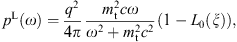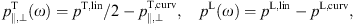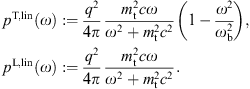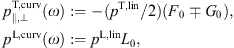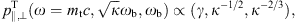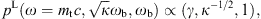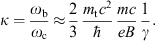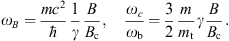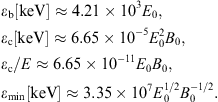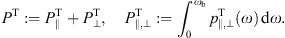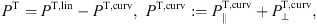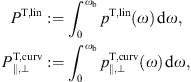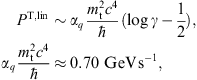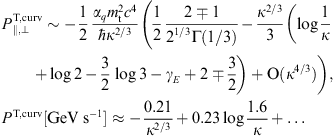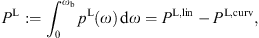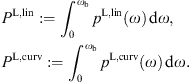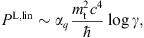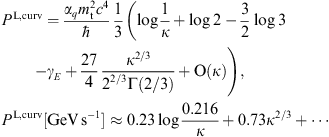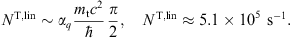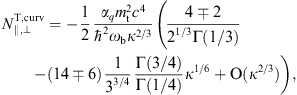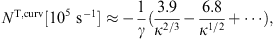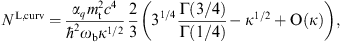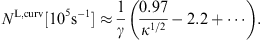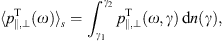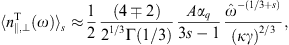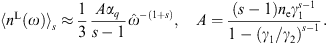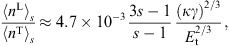Volume 23, Issue 1, February 2005, Pages 117-129
Abstract
Superluminal radiation emitted by electrons orbiting in strong magnetic fields is investigated. We show that electrons gyrating in the surface fields of rotation-powered neutron stars can radiate superluminal quanta (tachyons) via the synchrotron mechanism. The tachyonic luminosity of γ-ray pulsars is inferred from COMPTEL and EGRET observations, and so is the magnetospheric electron population generating this radiation. In the surface fields, electromagnetic synchrotron radiation in the γ-ray band is suppressed by a quantum cutoff, but not so tachyonic γ-radiation. This provides an exceptional opportunity to search for tachyon radiation, unspoiled by electromagnetic emission. Estimates of the superluminal power radiated and the tachyonic count rates are obtained for each of the seven established γ-ray pulsars, the Crab and Vela pulsars, as well as PSR B1706−44, Geminga, PSR B1055−52, B1951+32, and B1509−58. Detection mechanisms such as tachyonic ionization and Compton scattering are analyzed with regard to superluminal γ-rays.
Keywords: Superluminal curvature radiation; Tachyonic γ-rays; Longitudinal γ-radiation; Pulsar magnetospheres
PACS classification codes: 95.30.Gv; 41.60.Ap; 97.60.Gb
Article Outline
1. Introduction
When considering superluminal quanta, we may try a wave theory or a particle picture as starting point. The latter has been studied for quite some time, but did not result in viable interactions with matter [1], [2], [3], [4], [5] and [6]. Here, tachyons will be modeled as wave fields with negative mass-square, coupled by minimal substitution to subluminal particles. Interaction with matter is indeed the crucial point, we will maintain the best established interaction mechanism, minimal substitution, by treating tachyons like photons with negative mass square, a real Proca field minimally coupled to subluminal matter [7] and [8].
We will work out a specific example, tachyonic synchrotron emission from electrons gyrating in the surface fields of γ-ray pulsars. The detectors used to collect the γ-ray fluxes operated in adjacent or partly overlapping energy bands with very different mechanisms, ionization [9], Compton scattering [10], and electron-positron pair creation [11], and we will discuss the respective cross-sections with regard to tachyonic γ-rays. We will calculate the energy stored in the electron population gyrating in the surface magnetic fields, and relate the slope of the electronic power-law distribution to the frequency scaling of the tachyon flux. We will conclude from the break frequencies of the observed fluxes that the gyration energies can reach the low TeV range, and comment on cosmic ray acceleration in the magnetospheres.
In Section 2, we study superluminal synchrotron radiation from electrons subjected to high magnetic field strengths. We will introduce the tachyonic counterparts of certain quantities familiar from electromagnetic synchrotron radiation, such as critical frequencies, break frequencies and critical field strengths, and explain how they relate to the spectral densities, the tachyon mass, and the electronic Lorentz factor. In Section 3, we study the synchrotron power radiated in tachyonic γ-rays by the magnetospheric electron populations of γ-ray pulsars. We calculate the synchrotron power in the high-magnetic-field limit as well as the tachyonic count rates and average the tachyonic spectral densities with electronic power-law distributions. The tachyonic γ-ray luminosity is inferred from the measured fluxes and all that goes with it, such as the electronic power-law indices and the energy range of the gyrating electrons. In Section 4, we present our conclusions.
2. Tachyonic synchrotron radiation in strong magnetic fields
The superluminal spectral densities can be readily assembled
from the general formalism of tachyonic radiation theory [12] and [13], which will
not be repeated here, but we restate the densities in Figs. (2.1), (2.2), (2.3), (2.4), (2.5), (2.6), (2.7) and (2.8). There is
a low-and a high-frequency regime, separated by the break frequency ωb = γmtc,
where γ 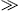 1 is the Lorentz factor of the
radiating ultra-relativistic source, typically a circularly orbiting
electron, and mt is the
tachyon mass. The latter has the dimension of an inverse length, being
a shortcut for mtc/
1 is the Lorentz factor of the
radiating ultra-relativistic source, typically a circularly orbiting
electron, and mt is the
tachyon mass. The latter has the dimension of an inverse length, being
a shortcut for mtc/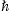 .
The subsequent spectral densities only apply in the range ω
.
The subsequent spectral densities only apply in the range ω 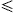 ωb.
There is also high-frequency radiation beyond this break frequency, but
this needs second quantization, as the high magnetic field strengths
considered here lead to an exponential cutoff of the classical
radiation. In the low-frequency regime, however, quantum effects are
perturbative, cf. after (2.10).
ωb.
There is also high-frequency radiation beyond this break frequency, but
this needs second quantization, as the high magnetic field strengths
considered here lead to an exponential cutoff of the classical
radiation. In the low-frequency regime, however, quantum effects are
perturbative, cf. after (2.10).
The transversal radiation can be split into two linear
polarization components,
The lower plus-sign in (2.2) refers to the
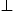 -polarization,
and q is the tachyonic charge of the electron. The
tachyon mass, mt ≈ 2.15 keV/c2,
and the ratio q2/e2 ≈ 1.4 × 10−11
of tachyonic and electric fine structure constants can be inferred from
Lamb shifts in hydrogenic systems [7]. The
spectral functions can be traced back to Airy functions,
-polarization,
and q is the tachyonic charge of the electron. The
tachyon mass, mt ≈ 2.15 keV/c2,
and the ratio q2/e2 ≈ 1.4 × 10−11
of tachyonic and electric fine structure constants can be inferred from
Lamb shifts in hydrogenic systems [7]. The
spectral functions can be traced back to Airy functions,where the argument ξ is a shortcut for
and ωb = eB/(γmc) is the gyrofrequency, cf. after (2.9). As mentioned, we restrict to frequencies ω
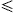 ωb.
The parameter κ will turn out to be the expansion
parameter for the power radiated, cf. Section 3. We will
consider the κ → 0 asymptotics,
attained in high magnetic fields. The spectral density of the
longitudinal radiation reads,
ωb.
The parameter κ will turn out to be the expansion
parameter for the power radiated, cf. Section 3. We will
consider the κ → 0 asymptotics,
attained in high magnetic fields. The spectral density of the
longitudinal radiation reads,with the spectral function L0(ξ) defined in Figs. (2.3) and (2.4). The ascending series and asymptotic limits of F0, G0 and L0 can be found in Ref. [13].
We split the densities Figs. (2.2) and (2.5) into a
linear and a curvature component,
The curvature radiation subtracted in (2.6) can be read off from Figs. (2.2) and (2.5),
where the upper minus-sign refers to
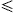 ωb,
cf. Ref. [12]. The three
densities
ωb,
cf. Ref. [12]. The three
densities We consider κ 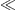 1,
cf. (2.4), but still
large enough that κγ2
1,
cf. (2.4), but still
large enough that κγ2 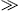 1. Since γ
1. Since γ 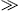 1 in the ultra-relativistic limit, we
can assume
1 in the ultra-relativistic limit, we
can assume ![]() ,
so that the mass term in the denominator of the spectral densities can
be dropped for frequencies
,
so that the mass term in the denominator of the spectral densities can
be dropped for frequencies ![]() .
Moreover, 0
.
Moreover, 0 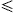 ξ(ω)
ξ(ω) 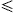 1
in the interval
1
in the interval ![]() ,
cf. (2.4), so that
,
cf. (2.4), so that ![]() and ξ(ωb) = 0.
Within this interval, the spectral functions ξ2/3F0,
ξ2/3G0
and L0 are of O(1) . Outside
this range, we find ξ
and ξ(ωb) = 0.
Within this interval, the spectral functions ξ2/3F0,
ξ2/3G0
and L0 are of O(1) . Outside
this range, we find ξ  1 for
1 for ![]() ,
so that the spectral functions can be replaced by their asymptotic
limits. There are three frequencies helpful to understand the
qualitative behavior of the spectral densities,
,
so that the spectral functions can be replaced by their asymptotic
limits. There are three frequencies helpful to understand the
qualitative behavior of the spectral densities,
where the three proportionality constants pertinent to the indicated choices of ω are of the same order. The densities decay ∝ ω for ω
 mtc.
The longitudinal density attains its maximum at ω ≈ mtc.
The transversal density also has its maximum at ω ≈ mtc,
followed by a minimum at about
mtc.
The longitudinal density attains its maximum at ω ≈ mtc.
The transversal density also has its maximum at ω ≈ mtc,
followed by a minimum at about  ωb,
if we replace the parentheses in (2.4) by an
absolute value. We then find ξ(ωb/κ) = 1,
where the ratio ωb/κ
is independent of the tachyon mass and coincides with the critical
photon frequency, ωc = (3/2)ωBγ3.
At about this frequency, the analytically continued transversal
spectral density attains a second maximum, like the electromagnetic
counterpart, before the exponential decay sets in. In actual fact, the
classical densities are exponentially cut off before this
high-frequency maximum is reached. This is a quantum effect arising in
the κ
ωb,
if we replace the parentheses in (2.4) by an
absolute value. We then find ξ(ωb/κ) = 1,
where the ratio ωb/κ
is independent of the tachyon mass and coincides with the critical
photon frequency, ωc = (3/2)ωBγ3.
At about this frequency, the analytically continued transversal
spectral density attains a second maximum, like the electromagnetic
counterpart, before the exponential decay sets in. In actual fact, the
classical densities are exponentially cut off before this
high-frequency maximum is reached. This is a quantum effect arising in
the κ  1
limit, due to the high magnetic field strength.
1
limit, due to the high magnetic field strength.
We shortly summarize the notation and the constants.
Gyroradius and gyrofrequency relate as R ≈ c/ωB,
where ωB = eB/(γmc),
and 1G · e ≈ 2.998 × 10−7 GeV cm−1.
We write γ = E/mc2,
so that eB ≈ E/R,
where E and m denote energy and
mass of the gyrating electron or positron, other possible source
particles like protons and heavier nuclei will not be considered. We
use the Heaviside–Lorentz system, so that e2/(4π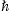 c) =: αe ≈ 1/137
and q2/(4π
c) =: αe ≈ 1/137
and q2/(4π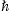 c) =: αq ≈ 1.0 × 10−13
are the electric and tachyonic fine structure constants. We restore the
mass unit in the above densities, mt → mtc/
c) =: αq ≈ 1.0 × 10−13
are the electric and tachyonic fine structure constants. We restore the
mass unit in the above densities, mt → mtc/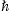 ≈ 1.09 × 108 cm−1,
so that the break frequency reads ωb = γmtc2/
≈ 1.09 × 108 cm−1,
so that the break frequency reads ωb = γmtc2/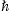 .
Finally, αq/αe ≈ 1.4 × 10−11
and mt ≈ m/238 ≈ 2.15 keV/c2.
.
Finally, αq/αe ≈ 1.4 × 10−11
and mt ≈ m/238 ≈ 2.15 keV/c2.
When calculating the power radiated, cf. Section 3, we will use κ
in (2.4) as
expansion parameter,
 1
as well as κγ2
1
as well as κγ2  1 usually apply, cf. Table 2. The
opposite limit, κ
1 usually apply, cf. Table 2. The
opposite limit, κ  1, is realized in planetary
magnetospheres and supernova remnants [13]. The
surface fields are quite comparable to the critical field, Bc = m2c3/(e
1, is realized in planetary
magnetospheres and supernova remnants [13]. The
surface fields are quite comparable to the critical field, Bc = m2c3/(e ) ≈ 4.414 × 1013
G, cf. Table 1. The
gyrofrequency and the ratio of critical and break energy relate to the
magnetic field ratio as
) ≈ 4.414 × 1013
G, cf. Table 1. The
gyrofrequency and the ratio of critical and break energy relate to the
magnetic field ratio asThis notation is kept close to electromagnetic synchrotron radiation [14], [15], [16] and [17], as is the whole formalism, of course. However, the spectral densities (2.2) applicable below the break frequency do not have an electromagnetic counterpart, only the upper frequency range has, but the high-frequency radiation requires second quantization in strong fields. Quantum corrections [18] are negligible for frequencies much smaller than the electron energy, which is the case below the break frequency. In the opposite limit,
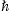 ω/E
ω/E 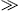 1, the classical spectral peak near the
critical frequency is wiped out by an exponential cutoff, as is the
electromagnetic synchrotron radiation [19]. Quantum
effects also lead to an attenuation of the classical radiation in the
cyclotron limit, for slowly gyrating source particles. The quantization
of tachyonic cyclotron and synchrotron radiation will be discussed
elsewhere.
1, the classical spectral peak near the
critical frequency is wiped out by an exponential cutoff, as is the
electromagnetic synchrotron radiation [19]. Quantum
effects also lead to an attenuation of the classical radiation in the
cyclotron limit, for slowly gyrating source particles. The quantization
of tachyonic cyclotron and synchrotron radiation will be discussed
elsewhere.
Setting the scales: break energy, critical energy and electronic Lorentz factor determining the shape of the tachyonic spectral densities, cf. (2.9)
| κ | κγ | κγ2 | εc/E | κlc | D (kpc) | |
|---|---|---|---|---|---|---|
| Crab | 1.67 × 10−5−k | 0.0326 | 6.37 × 101+k | 2.5 × 102+k | 6.7 × 101−k | 2.0 |
| Vela | 1.86 × 10−5−k | 0.0365 | 7.12 × 101+k | 2.3 × 102+k | 1.4 × 103−k | 0.3 |
| B1706−44 | 2.04 × 10−5−k | 0.0400 | 7.81 × 101+k | 2.1 × 102+k | 2.3 × 103−k | 1.82 |
| Geminga | 3.96 × 10−5−k | 0.0775 | 1.51 × 102+k | 1.1 × 102+k | 5.75 × 104−k | 0.16 |
| B1055−52 | 5.75 × 10−5−k | 0.113 | 2.20 × 102+k | 7.3 × 101+k | 4.9 × 104−k | 1.53 |
| B1951+32 | 1.29 × 10−4−k | 0.253 | 4.94 × 102+k | 3.3 × 101+k | 8.7 × 102−k | 2.50 |
| B1509−58 | 4.08 × 10−6−k | 8.00 × 10−3 | 1.56 × 101+k | 1.0 × 103+k | 1.5 × 103−k | 4.3 |
Input parameters as in Table 1. The
expansion parameter for the tachyonic powers and count rates is the
ratio εb/εc
of break and critical energy, denoted by κ, cf.
Figs. (2.4) and (2.10). The κ-expansions
in Section 3 apply for κ 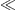 1
and κγ2
1
and κγ2 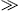 1, which defines constraints on the
electronic Lorentz factor, γ ≈ 1.96 × 103+k.
The product κγ occurring in the averaged tachyonic
spectral densities (3.12) is
independent of the electron energy. A large ratio εc/E
of critical and electron energy indicates that electromagnetic
synchrotron radiation and the resulting radiation damping is suppressed
by a quantum cutoff. κlc is
the expansion parameter for gyration in the light cylinder fields, cf. Table 1. For κlc
to be small, very high gyration and TeV γ-ray energies are required,
which are not observed in the pulsed emission. These light cylinder
fields and the surface fields of millisecond pulsars exemplify the
crossover between the asymptotic regimes studied here and in Ref. [13]. The pulsar
distance D(kpc) is taken from Ref. [26].
1, which defines constraints on the
electronic Lorentz factor, γ ≈ 1.96 × 103+k.
The product κγ occurring in the averaged tachyonic
spectral densities (3.12) is
independent of the electron energy. A large ratio εc/E
of critical and electron energy indicates that electromagnetic
synchrotron radiation and the resulting radiation damping is suppressed
by a quantum cutoff. κlc is
the expansion parameter for gyration in the light cylinder fields, cf. Table 1. For κlc
to be small, very high gyration and TeV γ-ray energies are required,
which are not observed in the pulsed emission. These light cylinder
fields and the surface fields of millisecond pulsars exemplify the
crossover between the asymptotic regimes studied here and in Ref. [13]. The pulsar
distance D(kpc) is taken from Ref. [26].
Entries as defined in Section 2: electron energy E(GeV) = 10k (input), surface field B (input), gyroradius R, tachyonic break energy εb(keV) ≈ 4.2 × 103+k, critical energy εc
| B (1012G) | R (cm) | εc (GeV) | εmin (keV) | P (ms) | Blc (G) | |
|---|---|---|---|---|---|---|
| Crab | 3.8 | 8.8 × 10−7+k | 2.5 × 102k+2 | 1.7 × 10k/2+1 | 33.40 | 9.4 × 105 |
| Vela | 3.4 | 9.8 × 10−7+k | 2.3 × 102k+2 | 1.8 × 10k/2+1 | 89.29 | 4.4 × 104 |
| B1706−44 | 3.1 | 1.1 × 10−6+k | 2.1 × 102k+2 | 1.9 × 10k/2+1 | 102.45 | 2.7 × 104 |
| Geminga | 1.6 | 2.1 × 10−6+k | 1.1 × 102k+2 | 2.65 × 10k/2+1 | 237.09 | 1.1 × 103 |
| B1055−52 | 1.1 | 3.0 × 10−6+k | 7.3 × 102k+1 | 3.2 × 10k/2+1 | 197.10 | 1.3 × 103 |
| B1951+32 | 0.49 | 6.8 × 10−6+k | 3.3 × 102k+1 | 4.8 × 10k/2+1 | 39.53 | 7.3 × 104 |
| B1509−58 | 15.5 | 2.15 × 10−7+k | 1.0 × 102k+3 | 8.5 × 10k/2 | 150.66 | 4.2 × 104 |
One may envisage −2 < k < 4 as typical range for the continuous parameter k labeling the electron energy. The transversal and longitudinal spectral peaks are located at the tachyon mass (2.15 keV), the minimum of the transversal tachyonic energy density is at εmin. The surface fields B and periods P are taken from Ref. [26], and Blc is the field strength at the light cylinder. With one exception, the listed pulsars are detected in hard γ-rays, with power-law spectra extending beyond 1 GeV: Crab (PSR B0531+21), Vela (PSR B0833−45), PSR B1706−44, Geminga (PSR B0633+17), PSR B1055−52, and PSR B1951+32. The γ-ray spectrum of the high-magnetic-field pulsar PSR B1509−58 is soft, cut off at about 10 MeV. The γ-ray fluxes of these pulsars are quoted in Section 3.
To get an overview regarding orders of magnitude, we define
the shortcuts E0 = E[GeV]
and B0 = B[G],
and write the preceding formulas as scaling relations in these
dimensionless numbers. For instance, ![]() and ωB[GHz] ≈ 29.98/R[cm].
Lorentz factor and expansion parameter scale as γ ≈ 1957E0
and
and ωB[GHz] ≈ 29.98/R[cm].
Lorentz factor and expansion parameter scale as γ ≈ 1957E0
and ![]() ,
respectively. We also note
,
respectively. We also note ![]() and κγ2 ≈ 2.42 × 1014E0/B0.
The energies attached to break and critical frequency and to the
transversal spectral minimum as defined after (2.9), εb,c,min =
and κγ2 ≈ 2.42 × 1014E0/B0.
The energies attached to break and critical frequency and to the
transversal spectral minimum as defined after (2.9), εb,c,min = 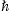 ωb,c,min,
scale as
ωb,c,min,
scale as
3. Tachyonic γ-rays from pulsar magnetospheres
We will study the tachyonic synchrotron power radiated by electrons gyrating in the surface magnetic fields of γ-ray pulsars, based on the spectral densities Figs. (2.1) and (2.5). The parameters of the individual pulsars are listed in Table 1 and Table 2. The radiated power and the tachyonic count rates calculated in Figs. (3.1), (3.2), (3.3), (3.4), (3.5), (3.6), (3.7), (3.8), (3.9) and (3.10) are stated in Table 3 for each of the known γ-ray pulsars, parametrized by the gyration energy. In Figs. (3.11), (3.12) and (3.13), we will average the tachyonic spectral densities with an electronic power-law distribution, and then proceed with a phenomenological discussion of the observed γ-ray fluxes, including the detection mechanisms of the γ-ray counters.
Superluminal power and tachyonic count rates
| P(GeV s−1) = PT + PL | N(105 s−1) = NT + NL | |
|---|---|---|
| Crab | PT ≈ 3.2 × 102k/3+2 + 1.1k + 2.3 | NT ≈ 5.1 + 3.05 × 10−k/3 − 8.5 × 10−k/2−1 |
| PL ≈ 3.1 + 1.1k − 4.8 × 10−2k/3−4 | NL ≈ 5.1 − 1.2 × 10−k/2−1 + 1.1 × 10−k−3 | |
| Vela | PT ≈ 3.0 × 102k/3+2 + 1.1k + 2.3 | NT ≈ 5.1 + 2.8 × 10−k/3 − 8.1 × 10−k/2−1 |
| PL ≈ 3.15 + 1.1k − 5.1 × 10−2k/3−4 | NL ≈ 5.1 − 1.15 × 10−k/2−1 + 1.1 × 10−k−3 | |
| B1706−44 | PT ≈ 2.8 × 102k/3+2 + 1.1k + 2.4 | NT ≈ 5.1 + 2.7 × 10−k/3 − 7.7 × 10−k/2−1 |
| PL ≈ 3.2 + 1.1k − 5.45 × 10−2k/3−4 | NL ≈ 5.1 − 1.1 × 10−k/2−1 + 1.1 × 10−k−3 | |
| Geminga | PT ≈ 1.8 × 102k/3+2 + 1.1k + 2.5 | NT ≈ 5.1 + 1.7 × 10−k/3−5.5 × 10−k/2−1 |
| PL ≈ 3.3 + 1.1k − 8.5 × 10−2k/3−4 | NL ≈ 5.1 − 7.9 × 10−k/2−2 + 1.1 × 10−k−3 | |
| B1055−52 | PT ≈ 1.4 × 102k/3+2 + 1.1k + 2.6 | NT ≈ 5.1 + 1.3 × 10−k/3 − 4.6 × 10−k/2−1 |
| PL ≈ 3.4 + 1.1k − 1.1 × 10−2k/3−3 | NL ≈ 5.1 − 6.5 × 10−k/2−2 + 1.1 × 10−k−3 | |
| B1951+32 | PT ≈ 8.2 × 102k/3+1 + 1.1k + 2.8 | NT ≈ 5.1 + 7.8 × 10−k/3−1 − 3.1 × 10−k/2−1 |
| PL ≈ 3.6 + 1.1k − 1.9 × 10−2k/3−3 | NL ≈ 5.1 − 4.4 × 10−k/2−2 + 1.1 × 10−k−3 | |
| B1509−58 | PT ≈ 8.2 × 102k/3+2 + 1.1k + 2.0 | NT ≈ 5.1 + 7.8 × 10−k/3 − 1.7 × 10−k/2 |
| PL ≈ 2.8 + 1.1k − 1.9 × 10−2k/3−4 | NL ≈ 5.1 − 2.45 × 10−k/2−1 + 1.1 × 10−k−3 |
Input parameters as in Table 1 and Table 2, the parameter k refers to the electron energy, E = 10k GeV. The transversal (unpolarized) and longitudinal powers PT,L(GeV s−1) include linear and curvature radiation, cf. Section 3. The corresponding tachyonic count rates are denoted by NT,L(105 s−1). For comparison, the superluminal power transversally and longitudinally radiated by an electron in straight uniform motion with the same Lorentz factor reads PT,lin(GeV s−1) ≈ 1.6k + 4.95 and PL,lin(GeV s−1) ≈ 1.6k + 5.3, respectively [13]. The curvature radiation is obtained by subtracting these linear powers from PT,L. The linear count rates NT,L,lin approach a constant value of 5.1 × 105 s−1 in the ultra-relativistic limit.
We start with the integration of the transversal spectral
density (2.1). The power
radiated by a single gyrating electron can be split into linear
polarization components,
so that
which is the leading order in the ultra-relativistic 1/γ-expansion of the first integral in (3.2), cf. Ref. [12]. We have restored the natural units, mt → mtc/
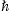 ;
the tachyonic fine structure constant αq
is defined before (2.10). The
second integral in (3.2) gives the
transversal curvature radiation,
;
the tachyonic fine structure constant αq
is defined before (2.10). The
second integral in (3.2) gives the
transversal curvature radiation,The lower plus-sign in (3.4) refers to the
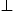 -polarization,
and PT,curv is the total
transversally polarized curvature radiation, cf. (3.2). The
expansion parameter κ, the ratio of break and
critical frequency, is defined in (2.10), and γE ≈ 0.5772.
-polarization,
and PT,curv is the total
transversally polarized curvature radiation, cf. (3.2). The
expansion parameter κ, the ratio of break and
critical frequency, is defined in (2.10), and γE ≈ 0.5772.
The longitudinal radiant power can likewise be decomposed into
a linear and a curvature term, cf. (2.6),
An elementary integration gives the linear power,
up to O(γ−1) like in (3.3). The κ-expansion of the longitudinal curvature radiation reads,
The total power radiated is P = PT+PL, with the polarized powers PT,L, cf. Figs. (3.2) and (3.5).
The count rates are composed like in Figs. (3.2) and (3.5), with the
spectral densities divided by 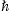 ω;
we write the transversal count as NT = NT,lin − NT,curv,
where
ω;
we write the transversal count as NT = NT,lin − NT,curv,
where ![]() .
The linear count is constant in leading order, in the
ultra-relativistic regime that is,
.
The linear count is constant in leading order, in the
ultra-relativistic regime that is,
where we used αqmtc2/
 ≈ 3.27 × 105 s−1,
cf. before (2.10). The
longitudinal count rate, NL = NL,lin − NL,curv,
is composed of the linear count, NL,lin
≈ 3.27 × 105 s−1,
cf. before (2.10). The
longitudinal count rate, NL = NL,lin − NL,curv,
is composed of the linear count, NL,lin  NT,lin,
and the curvature term
NT,lin,
and the curvature termIn Table 2, the expansion parameter κ is listed for the individual pulsars, parametrized by the electronic gyration energy. In Table 3, we list the above expansions parametrized accordingly, which gives an overview as to how the magnetic field strengths and electron energies impact the weight of the linear and curvature terms. The range of electron energies (k-interval) for these expansions to apply can be read off from Table 2 for each pulsar.
To connect to γ-ray fluxes from magnetospheric electron
populations, we need to know the tachyonic spectral densities generated
by a non-singular electron distribution. To this end, we average the
densities Figs. (2.2) and (2.5) with an
electronic power-law, dn(γ) = Aγ−s dγ,
of index s > 1. The
ultra-relativistic electronic Lorentz factors range in a finite
interval, γ1 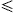 γ
γ 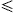 γ2,
with γ1
γ2,
with γ1  1; the normalization constant A
relates to the electron count in this interval as stated in (3.12). The
transversal density is averaged as
1; the normalization constant A
relates to the electron count in this interval as stated in (3.12). The
transversal density is averaged as
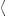 pL(ω)
pL(ω) s
is defined in the same way. We will focus on the number densities
s
is defined in the same way. We will focus on the number densities 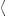 nL (ω)
nL (ω) s =
s =  pL(ω)
pL(ω) s/(
s/( ω),
since scaling exponents for γ-rays are usually defined with regard to
differential number counts. We restore the natural units, mt → mtc/
ω),
since scaling exponents for γ-rays are usually defined with regard to
differential number counts. We restore the natural units, mt → mtc/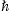 ,
and use the fine structure constant αq = q2/(4π
,
and use the fine structure constant αq = q2/(4π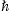 c)
and the scaling variable
c)
and the scaling variable This frequency scaling, the leading order asymptotics of the integrals (3.11), is valid in the range
with s > 1. The constant κγ is listed in Table 2 for the respective pulsars, and the tachyon energy, Et =
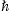 ω,
is meant in MeV units. In the frequency bands studied in the subsequent
examples of γ-ray pulsars, this ratio is well below 10−2,
so that we will focus on the transversal radiation only. The
transversal densities
ω,
is meant in MeV units. In the frequency bands studied in the subsequent
examples of γ-ray pulsars, this ratio is well below 10−2,
so that we will focus on the transversal radiation only. The
transversal densities  γ1/κ(γ1).
For these indices, the radiation is likewise overwhelmingly
transversal.
γ1/κ(γ1).
For these indices, the radiation is likewise overwhelmingly
transversal.
We denote the energy of the tachyonic γ-rays by Et
as in (3.13). The
tachyon flux, F = dN/dEt,
is derived from the normalized differential number count dN = (4πD2)−1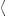 nT(ω)
nT(ω)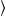 s dω,
where
s dω,
where ![]() stands for the total (unpolarized) transversal radiation, cf. (3.12), and D
is the distance to the pulsar, cf. Table 2.
Concerning units, we choose
stands for the total (unpolarized) transversal radiation, cf. (3.12), and D
is the distance to the pulsar, cf. Table 2.
Concerning units, we choose ![]() ,
where Et is in MeV, and the
measured proportionality factor and scaling exponent will be specified
below for the enumerated pulsars. These units will be used throughout,
mostly without mentioning. The scaling exponent relates to the electron
index as α = 1/3 + s,
cf. (3.12), and the
dimensionless number density can be retrieved from the flux and the
distance,
,
where Et is in MeV, and the
measured proportionality factor and scaling exponent will be specified
below for the enumerated pulsars. These units will be used throughout,
mostly without mentioning. The scaling exponent relates to the electron
index as α = 1/3 + s,
cf. (3.12), and the
dimensionless number density can be retrieved from the flux and the
distance, 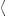 nT(ω)
nT(ω)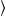 s = 4πD2
s = 4πD2 F;
we will infer the electronic source count ne
by equating
F;
we will infer the electronic source count ne
by equating ![]() in (3.12) with
in (3.12) with
In the following case study of the seven established γ-ray
pulsars, the observational input will be the amplitude and the scaling
exponent of the measured flux, ![]() ,
the energy band for a scaling exponent to apply, as well as the
spectral breaks where different power-laws join. We will determine the
electron distributions generating the radiation in the respective
frequency bands, in particular the electronic source count, that is,
the number of gyrating electrons generating the tachyon flux or a
power-law component of it. When inferring the electronic source number
from the measured fluxes, we have to take into account that only a
fraction αq/αe
(ratio of tachyonic and photonic fine structure constants, cf. before (2.10)) of the
tachyon flux passing through the detectors is absorbed. This requires a
rescaling of the electron count ne
by αe/αq ≈ 7.3 × 1010,
where ne is based on the
tachyon count in the detectors. That is, the electronic source count ne
is calculated, via Figs. (3.14) and (3.12), from the
observed flux F, but the actual tachyon flux is by
a factor of αe/αq
larger than the observed one, so that the actual number of synchrotron
electrons in the surface magnetic field is Ne ≈ neαe/αq.
,
the energy band for a scaling exponent to apply, as well as the
spectral breaks where different power-laws join. We will determine the
electron distributions generating the radiation in the respective
frequency bands, in particular the electronic source count, that is,
the number of gyrating electrons generating the tachyon flux or a
power-law component of it. When inferring the electronic source number
from the measured fluxes, we have to take into account that only a
fraction αq/αe
(ratio of tachyonic and photonic fine structure constants, cf. before (2.10)) of the
tachyon flux passing through the detectors is absorbed. This requires a
rescaling of the electron count ne
by αe/αq ≈ 7.3 × 1010,
where ne is based on the
tachyon count in the detectors. That is, the electronic source count ne
is calculated, via Figs. (3.14) and (3.12), from the
observed flux F, but the actual tachyon flux is by
a factor of αe/αq
larger than the observed one, so that the actual number of synchrotron
electrons in the surface magnetic field is Ne ≈ neαe/αq.
The three telescopes employed in measuring the fluxes in the
various energy bands cited below operated with very different detection
mechanisms, but the rescaling of the observed fluxes withαe/αq
applies to all of them. In the OSSE detector [9], the basic
interaction was ionization generating scintillations in NaI(Tl)
crystals. COMPTEL [10] was a
counter based on Compton scattering, and the EGRET telescope [11] counted
γ-rays by conversion into electron-positron pairs. The crucial point
here is, that the cross-sections for ultra-relativistic
photoionization, photonic Compton scattering and photonic pair
production also apply to transversal tachyons, with the mentioned
rescaling by αq/αe.
The tachyon mass drops out in the dispersion relation, k2 = ω2/c2 + (mtc/ )2,
at γ-ray energies, which only makes an overall rescaling of the
respective photonic cross-sections [24] necessary.
This rescaling also shows in the non-relativistic limit, derived for
tachyonic ionization in Ref. [25], where we
also studied the effect of the tachyon mass in the low-energy (soft
X-ray) regime. The same rescaling of the Compton cross-section
(Klein–Nishina formula) can be traced back to classical Thomson
scattering, that is, to the acceleration of an electron by the incoming
tachyonic wave field, which triggers electromagnetic radiation [8]. Despite the
fact that the photonic cross-sections of the three mentioned processes
scale with higher powers of the electric fine structure constant, the
tachyonic counterpart is obtained in all three cases by an αq/αe-rescaling,
for transversal γ-rays at least; this is further discussed in the
Conclusion.
)2,
at γ-ray energies, which only makes an overall rescaling of the
respective photonic cross-sections [24] necessary.
This rescaling also shows in the non-relativistic limit, derived for
tachyonic ionization in Ref. [25], where we
also studied the effect of the tachyon mass in the low-energy (soft
X-ray) regime. The same rescaling of the Compton cross-section
(Klein–Nishina formula) can be traced back to classical Thomson
scattering, that is, to the acceleration of an electron by the incoming
tachyonic wave field, which triggers electromagnetic radiation [8]. Despite the
fact that the photonic cross-sections of the three mentioned processes
scale with higher powers of the electric fine structure constant, the
tachyonic counterpart is obtained in all three cases by an αq/αe-rescaling,
for transversal γ-rays at least; this is further discussed in the
Conclusion.
Apart from the electronic source count and the total gyration
energy, ![]() ,
stored in these electrons, we will determine their tachyonic γ-ray
luminosity, the power transversally radiated in a given frequency band,
,
stored in these electrons, we will determine their tachyonic γ-ray
luminosity, the power transversally radiated in a given frequency band,
We start with the Crab pulsar. The flux in the
30–4000 MeV interval scales as ![]() ,
cf. Refs. [27] and [28], suggesting
an electron index s ≈ 1.72. As
pointed out after (3.14), the
observed flux has still to be rescaled by a factor of αe/αq ≈ 7.3 × 1010,
as most tachyons pass unnoticed through the detectors. The cited
interval boundaries correspond to electron energies of 100.85
and 103.0 GeV, respectively. There is a
spectral break at 30 MeV, followed by a second power-law,
,
cf. Refs. [27] and [28], suggesting
an electron index s ≈ 1.72. As
pointed out after (3.14), the
observed flux has still to be rescaled by a factor of αe/αq ≈ 7.3 × 1010,
as most tachyons pass unnoticed through the detectors. The cited
interval boundaries correspond to electron energies of 100.85
and 103.0 GeV, respectively. There is a
spectral break at 30 MeV, followed by a second power-law, ![]() ,
in the 0.12–30 MeV band, cf. Refs. [29] and [30]. This flux
component is generated by electrons gyrating with energies from 10−1.55
to 100.85 GeV, with power-law index s ≈ 1.92.
The tachyonic spectral densities above and below the spectral break
relate to the amplitudes of the respective electronic power-laws as
,
in the 0.12–30 MeV band, cf. Refs. [29] and [30]. This flux
component is generated by electrons gyrating with energies from 10−1.55
to 100.85 GeV, with power-law index s ≈ 1.92.
The tachyonic spectral densities above and below the spectral break
relate to the amplitudes of the respective electronic power-laws as ![]() and
and ![]() ,
cf. (3.12). The
normalization constants of the electron distributions in the adjacent
intervals above and below the break energy (of 100.85 GeV)
read Aα=2.05 ≈ 690ne
and Aα=2.25 ≈ 36.9ne,
respectively. We find ne ≈ 1.4 × 1035
in the upper interval (where
,
cf. (3.12). The
normalization constants of the electron distributions in the adjacent
intervals above and below the break energy (of 100.85 GeV)
read Aα=2.05 ≈ 690ne
and Aα=2.25 ≈ 36.9ne,
respectively. We find ne ≈ 1.4 × 1035
in the upper interval (where ![]() )
and ne ≈ 2.0 × 1037
below the break energy (where
)
and ne ≈ 2.0 × 1037
below the break energy (where ![]() ).
These electron counts are calculated by equating flux and number
density, cf. Figs. (3.14) and (3.12), and they
still have to be renormalized; the actual count in the 100.85−103.0 GeV
range reads
).
These electron counts are calculated by equating flux and number
density, cf. Figs. (3.14) and (3.12), and they
still have to be renormalized; the actual count in the 100.85−103.0 GeV
range reads ![]() ,
and
,
and ![]() is the count below the break energy, in the 10−1.55−100.85 GeV
interval. The total electronic energy in the surface magnetic field is
calculated as indicated before (3.15); we find
is the count below the break energy, in the 10−1.55−100.85 GeV
interval. The total electronic energy in the surface magnetic field is
calculated as indicated before (3.15); we find ![]() above the break energy, and
above the break energy, and ![]() below. The respective electron populations produce the tachyonic
luminosity
below. The respective electron populations produce the tachyonic
luminosity ![]() in the 30–4000 MeV band, and
in the 30–4000 MeV band, and ![]() in the 0.12–30 MeV interval, cf. (3.15). These
gyration energies and luminosities are based on the observed flux F;
the actual tachyon flux is by a factor of αe/αq
higher, so that we have to replace the
in the 0.12–30 MeV interval, cf. (3.15). These
gyration energies and luminosities are based on the observed flux F;
the actual tachyon flux is by a factor of αe/αq
higher, so that we have to replace the ![]() by the renormalized counts
by the renormalized counts ![]() .
.
Remarks. There is no superluminal radiation damping that could slow down the gyration, as the tachyonic Green function is time symmetric. The energy radiated stems from the oscillators of the cosmic absorber [25] and [31]. The absorber field breaks the time symmetry and renders the interaction causal and non-local [8]. The latter has implications on energy conservation, as the radiated energy is drained from the absorber. For this reason, the search for missing negative mass-squares suggested in Ref. [4] fails, where bubble-chamber events were reanalyzed, assuming a local but otherwise unspecified interaction of tachyons with matter, discounting the time symmetry of the Green function outside the light cone. Had there been detection in these experiments, in the relativistic framework in which they were interpreted, this would have been tantamount to causality violation. The radiation mechanism scrutinized here, based on a Proca field with negative mass-square minimally coupled to subluminal matter, is non-relativistic. It implies the absolute spacetime defined by the absorber [5] and [6], even though the Lagrangians are still covariant. Finally, electromagnetic synchrotron radiation would lead to radiation damping, but is suppressed by a quantum cutoff, cf. after (2.11).
There is a further spectral break at 0.12 MeV, where
the spectrum flattens to ![]() ,
cf. Ref. [29], and then
continues as an unbroken power-law even into the soft X-ray band [32] and [33]. The
radiation below 0.12 MeV is not accessible in the
ultra-relativistic limit because of the moderate electronic Lorentz
factors; the spectral densities would have to be recalculated, with the
Nicholson asymptotics replaced by Debye’s approximation of large-order
Bessel functions [34]. At the
opposite end, above 4000 MeV, there is some indication that
the radiation terminates in a steep spectral slope, and no pulsed
emission is detected in the TeV region [28]. The fluxes
used here and in the subsequent examples refer to the pulsed emission,
and they are phase averages. Phase-resolved spectra exist for the Crab
and Vela pulsars and Geminga. As for the Crab pulsar, the
phase-dependent exponents α range from 1.42 to 2.65
in the 30–4000 MeV band [27], and from
2.16 to 2.41 in the 0.12–30 MeV interval, cf. Ref. [29]. The
respective phase-resolved electron indices, s = α − 1/3,
are usually larger than 1, and they never fall below 1/3, cf. after (3.13).
,
cf. Ref. [29], and then
continues as an unbroken power-law even into the soft X-ray band [32] and [33]. The
radiation below 0.12 MeV is not accessible in the
ultra-relativistic limit because of the moderate electronic Lorentz
factors; the spectral densities would have to be recalculated, with the
Nicholson asymptotics replaced by Debye’s approximation of large-order
Bessel functions [34]. At the
opposite end, above 4000 MeV, there is some indication that
the radiation terminates in a steep spectral slope, and no pulsed
emission is detected in the TeV region [28]. The fluxes
used here and in the subsequent examples refer to the pulsed emission,
and they are phase averages. Phase-resolved spectra exist for the Crab
and Vela pulsars and Geminga. As for the Crab pulsar, the
phase-dependent exponents α range from 1.42 to 2.65
in the 30–4000 MeV band [27], and from
2.16 to 2.41 in the 0.12–30 MeV interval, cf. Ref. [29]. The
respective phase-resolved electron indices, s = α − 1/3,
are usually larger than 1, and they never fall below 1/3, cf. after (3.13).
The Vela pulsar radiates a flux of ![]() in the 30–2000 MeV interval, cf. Refs. [27] and [35], generated
by electrons in the 100.85–102.7 GeV
range with power-law index s ≈ 1.29.
The normalization of the electron distribution in this range is A ≈ 6.32ne,
and the electronic source count reads ne ≈ 5.9 × 1033
or Ne ≈ 4.3 × 1044
if renormalized. These electrons store an energy of Ee[erg] ≈ 0.125Ne
and generate the number density
in the 30–2000 MeV interval, cf. Refs. [27] and [35], generated
by electrons in the 100.85–102.7 GeV
range with power-law index s ≈ 1.29.
The normalization of the electron distribution in this range is A ≈ 6.32ne,
and the electronic source count reads ne ≈ 5.9 × 1033
or Ne ≈ 4.3 × 1044
if renormalized. These electrons store an energy of Ee[erg] ≈ 0.125Ne
and generate the number density ![]() ,
which results in a tachyonic γ-ray luminosity of Lt[erg/s] ≈ 10.4Ne
in the 30–2000 MeV band. The phase-resolved exponents of this
pulsar range from 1.38 to 2.21, cf. Ref. [27]. Pulsed TeV
radiation is not detectable [36].
,
which results in a tachyonic γ-ray luminosity of Lt[erg/s] ≈ 10.4Ne
in the 30–2000 MeV band. The phase-resolved exponents of this
pulsar range from 1.38 to 2.21, cf. Ref. [27]. Pulsed TeV
radiation is not detectable [36].
γ-Radiation from PSR B1706−44 has been detected from
50 MeV up to 20 GeV, cf. Ref. [37]. A flux ![]() is observed in the 50–1000 MeV interval, corresponding to
electron energies from 101.1 to 102.4 GeV.
This is the only example where the (phase-averaged) electron index
drops below 1, s ≈ 0.94. The
electronic power-law normalization in the indicated GeV range is Aα=1.27 ≈ 0.160ne,
and the tachyonic number density scales as
is observed in the 50–1000 MeV interval, corresponding to
electron energies from 101.1 to 102.4 GeV.
This is the only example where the (phase-averaged) electron index
drops below 1, s ≈ 0.94. The
electronic power-law normalization in the indicated GeV range is Aα=1.27 ≈ 0.160ne,
and the tachyonic number density scales as ![]() in the 50–1000 MeV interval. There is a spectral break at
1000 MeV, followed by a second flux component,
in the 50–1000 MeV interval. There is a spectral break at
1000 MeV, followed by a second flux component, ![]() ,
cf. Ref. [37], which
applies up to 20 GeV, suggesting electron energies up to 103.7 GeV
in the surface field. This flux is generated by an electronic power-law
of index s ≈ 1.92 and amplitude Aα=2.25 ≈ 1.54 × 105ne
in the 102.4–103.7 GeV
range. The tachyonic number density in the 1–20 GeV interval
reads
,
cf. Ref. [37], which
applies up to 20 GeV, suggesting electron energies up to 103.7 GeV
in the surface field. This flux is generated by an electronic power-law
of index s ≈ 1.92 and amplitude Aα=2.25 ≈ 1.54 × 105ne
in the 102.4–103.7 GeV
range. The tachyonic number density in the 1–20 GeV interval
reads ![]() .
By the way, the frequency scaling is obtained by substituting
.
By the way, the frequency scaling is obtained by substituting  ω/1 MeV
for Et. Both electronic
power-laws admit the same source number, ne ≈ 9.2 × 1033,
valid for s ≈ 0.94 as well as s ≈ 1.92;
the renormalized source count for each of these slopes is accordingly Ne ≈ 6.7 × 1044.
These electron populations below and above the break energy of 102.4 GeV
contain a gyration energy of
ω/1 MeV
for Et. Both electronic
power-laws admit the same source number, ne ≈ 9.2 × 1033,
valid for s ≈ 0.94 as well as s ≈ 1.92;
the renormalized source count for each of these slopes is accordingly Ne ≈ 6.7 × 1044.
These electron populations below and above the break energy of 102.4 GeV
contain a gyration energy of ![]() and
and ![]() ,
respectively; they produce a tachyonic luminosity of
,
respectively; they produce a tachyonic luminosity of ![]() in the 50–1000 MeV band, and of
in the 50–1000 MeV band, and of ![]() above the spectral break.
above the spectral break.
Geminga generates the flux ![]() in the 30–2000 MeV band, corresponding to electron energies
between 100.85 and 102.7 GeV,
cf. Refs. [27], [38] and [39]. This flux
allows us to infer the electron index, s ≈ 1.09,
and the tachyonic number density,
in the 30–2000 MeV band, corresponding to electron energies
between 100.85 and 102.7 GeV,
cf. Refs. [27], [38] and [39]. This flux
allows us to infer the electron index, s ≈ 1.09,
and the tachyonic number density, ![]() .
The electronic power-law normalization in the mentioned GeV interval is
A ≈ 0.649ne,
with source count ne ≈ 7.9 × 1032.
We find the renormalized electron count, Ne ≈ 5.8 × 1043,
the total energy of these electrons, Ee[erg] ≈ 0.16Ne,
as well as their tachyonic γ-ray luminosity in the 30–2000 MeV
interval, Lt[erg/s] ≈ 9.6Ne.
The power-law indices of the phase-resolved flux range from 1.27 to
1.89, cf. Ref. [27].
.
The electronic power-law normalization in the mentioned GeV interval is
A ≈ 0.649ne,
with source count ne ≈ 7.9 × 1032.
We find the renormalized electron count, Ne ≈ 5.8 × 1043,
the total energy of these electrons, Ee[erg] ≈ 0.16Ne,
as well as their tachyonic γ-ray luminosity in the 30–2000 MeV
interval, Lt[erg/s] ≈ 9.6Ne.
The power-law indices of the phase-resolved flux range from 1.27 to
1.89, cf. Ref. [27].
PSR B1055−52 radiates the flux ![]() in the 70–1000 MeV band [40], generated
by electrons cycling with energies from 101.2 to
102.4 GeV. In this range, we infer an
electronic power-law distribution of index s ≈ 1.25,
normalization Aα=1.58 ≈ 6.65ne,
and source number ne ≈ 4.4 × 1033,
which produces the tachyonic number density
in the 70–1000 MeV band [40], generated
by electrons cycling with energies from 101.2 to
102.4 GeV. In this range, we infer an
electronic power-law distribution of index s ≈ 1.25,
normalization Aα=1.58 ≈ 6.65ne,
and source number ne ≈ 4.4 × 1033,
which produces the tachyonic number density ![]() in the 70–1000 MeV interval. Above the spectral break at
1000 MeV, the flux scales as
in the 70–1000 MeV interval. Above the spectral break at
1000 MeV, the flux scales as ![]() up to at least 4000 MeV, cf. Ref. [40]. This means
electron energies up to 103.0 GeV in
the surface field, an electronic power-law index s ≈ 1.71
above the electronic break energy of 102.4 GeV,
and a tachyonic number density of
up to at least 4000 MeV, cf. Ref. [40]. This means
electron energies up to 103.0 GeV in
the surface field, an electronic power-law index s ≈ 1.71
above the electronic break energy of 102.4 GeV,
and a tachyonic number density of ![]() in the 1000–4000 MeV interval. The electronic power-law
normalization in the 102.4−103.0 GeV
range reads Aα=2.04 ≈ 1.15 × 104ne,
with ne ≈ 1.5 × 1033.
Below the electronic break energy, we count
in the 1000–4000 MeV interval. The electronic power-law
normalization in the 102.4−103.0 GeV
range reads Aα=2.04 ≈ 1.15 × 104ne,
with ne ≈ 1.5 × 1033.
Below the electronic break energy, we count ![]() electrons, which store a total energy of
electrons, which store a total energy of ![]() and radiate a power of
and radiate a power of ![]() in tachyonic γ-rays in the 70–1000 MeV band. Above the break
energy, there are
in tachyonic γ-rays in the 70–1000 MeV band. Above the break
energy, there are ![]() electrons gyrating in the 102.4–103.0 GeV
range, which add up to an electronic energy of
electrons gyrating in the 102.4–103.0 GeV
range, which add up to an electronic energy of ![]() and produce a tachyonic luminosity of
and produce a tachyonic luminosity of ![]() in the 1000–4000 MeV interval.
in the 1000–4000 MeV interval.
γ-radiation from PSR B1951+32 has been detected in a wide
band, from 10 MeV to 20 GeV, cf. Refs. [41] and [42], generated
by electrons gyrating in the 100.38–103.7 GeV
range. The flux scales as ![]() ,
cf. Ref. [41], seemingly
without a spectral break in this band. We find the electron index s ≈ 1.41,
the electronic power-law normalization A ≈ 13.2ne,
and the tachyonic number density
,
cf. Ref. [41], seemingly
without a spectral break in this band. We find the electron index s ≈ 1.41,
the electronic power-law normalization A ≈ 13.2ne,
and the tachyonic number density ![]() ,
from which we infer the electronic source count ne ≈ 6.2 × 1034
or Ne ≈ 4.5 × 1045
when renormalized. The gyration energy of these electrons is Ee[erg] ≈ 0.25Ne,
and their tachyonic radiation power in the
10 MeV–20 GeV interval amounts to Lt[erg/s] ≈ 2.9Ne.
A spectral break must occur below 10 MeV, according to the upper flux
limits derived in Refs. [43] and [44]; no pulsed
TeV radiation has been found [45].
,
from which we infer the electronic source count ne ≈ 6.2 × 1034
or Ne ≈ 4.5 × 1045
when renormalized. The gyration energy of these electrons is Ee[erg] ≈ 0.25Ne,
and their tachyonic radiation power in the
10 MeV–20 GeV interval amounts to Lt[erg/s] ≈ 2.9Ne.
A spectral break must occur below 10 MeV, according to the upper flux
limits derived in Refs. [43] and [44]; no pulsed
TeV radiation has been found [45].
PSR B1509−58 is not detected in hard γ-rays, possibly due to a
quantum cutoff inflicted by its high magnetic field, but this needs
further investigation in second quantization, cf. after (2.11). The
observed flux, ![]() ,
extends from 0.2 to 10 MeV, cf. Refs. [46] and [47], and is
produced by electrons with energies in the 10−1.3–100.38 GeV
range. We infer an electronic power-law of index s ≈ 1.35
and normalization A ≈ 2.25ne,
where ne ≈ 1.75 × 1036,
as well as a tachyonic number density of
,
extends from 0.2 to 10 MeV, cf. Refs. [46] and [47], and is
produced by electrons with energies in the 10−1.3–100.38 GeV
range. We infer an electronic power-law of index s ≈ 1.35
and normalization A ≈ 2.25ne,
where ne ≈ 1.75 × 1036,
as well as a tachyonic number density of ![]() in the mentioned MeV band. We note the electron count in the surface
field, Ne ≈ 1.3 × 1047,
the energy stored in these electrons, Ee[erg] ≈ 6.5 × 10−4Ne,
and their tachyonic luminosity, Lt[erg/s] ≈ 0.82Ne,
in the 0.2–10 MeV interval. Above 10 MeV, there is a
steep spectral break [47], and no
pulsed TeV radiation is observed [48]. At the
lower end, at 0.2 MeV, there is likewise a spectral break,
where the spectrum hardens, admitting a spectral index of about α ≈ 1.3
in the hard X-ray band [49] and [50], but this
radiation is not accessible in the ultra-relativistic synchrotron limit
[34].
in the mentioned MeV band. We note the electron count in the surface
field, Ne ≈ 1.3 × 1047,
the energy stored in these electrons, Ee[erg] ≈ 6.5 × 10−4Ne,
and their tachyonic luminosity, Lt[erg/s] ≈ 0.82Ne,
in the 0.2–10 MeV interval. Above 10 MeV, there is a
steep spectral break [47], and no
pulsed TeV radiation is observed [48]. At the
lower end, at 0.2 MeV, there is likewise a spectral break,
where the spectrum hardens, admitting a spectral index of about α ≈ 1.3
in the hard X-ray band [49] and [50], but this
radiation is not accessible in the ultra-relativistic synchrotron limit
[34].
4. Conclusion
We have given a quantitative and in part phenomenological discussion of superluminal synchrotron radiation in strong magnetic fields. We will further comment on the interaction of tachyons with matter, on the basis of the three detectors used to infer the magnetospheric electron populations and their tachyonic γ-ray luminosity. The ionization in the scintillation crystals of the OSSE counter [9] happens in the relativistic regime. OSSE operated above a 50 keV threshold, so that the tachyon mass of 2 keV can be neglected in the dispersion relation, given that only the squared energies enter, cf. before (3.15). Therefore, the relativistic photonic ionization cross-section [24] can be used for transversal tachyons, if properly rescaled. The only change necessary for tachyonic X-rays or γ-rays above 50 keV is a rescaling with the ratio of tachyonic and electric fine structure constant. This rescaling can be traced back to the non-relativistic limit, which depends on the tachyon mass and applies in the soft and hard X-ray bands [25]. The longitudinal relativistic cross-section has to be calculated from scratch without reference to a zero-mass limit [51]. The tachyon flux generated by synchrotron radiation in the surface fields of γ-ray pulsars is overwhelmingly transversally polarized, cf. (3.13), in contrast to the low-magnetic-field limit [13], and therefore we have not attempted a quantitative study of the longitudinal fraction beyond some basic estimates.
Compton scattering and pair creation were employed in the COMPTEL and EGRET detectors [10] and [11]. The tachyonic Thomson cross-section, the non-relativistic classical limit of Compton scattering, was derived in Ref. [8], but a quantum mechanical version is still lacking, especially if the incident tachyonic X-rays have energies close to the tachyon mass. In the relativistic regime, for γ-rays above 0.75 MeV (the threshold of the COMPTEL counter), the transversal cross-section is obtained by a rescaling of the Klein–Nishina formula with αq/αe, the same rescaling that applies to the Thomson and ionization cross-sections. The EGRET detector was a spark chamber recording electron-positron pairs produced by γ-rays scattered in tantalum foils. The conversion of tachyons into electron-positron pairs has not been studied in any limit and context as yet. However, one can reckon from the foregoing that the cross-section for the conversion of transversal γ-rays is just the Bethe–Heitler formula rescaled with αq/αe; the fluxes collected by EGRET were in the 20 MeV–30 GeV range, so that the tachyon mass is negligible in the dispersion relation. This rescaling of the EGRET fluxes is also suggested by cross-calibration with the COMPTEL detector, to avoid discontinuities in the band overlap.
Tachyonic synchrotron radiation above the break frequency has not been discussed here, cf. after (2.9) and Ref. [13]. This requires second quantization in strong magnetic fields, as quantum corrections in the high-frequency regime cannot be treated perturbatively. Above the break frequency, the classical radiation theory is severely modified by a quantum cutoff, which results in exponential decay of the spectral densities at the critical energy, where the classical spectral functions are peaked. This quantum cutoff may well be the reason that no pulsed TeV radiation is detected from the known γ-ray pulsars.