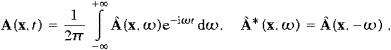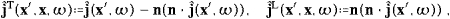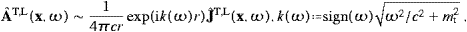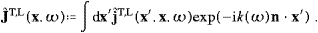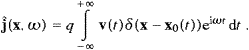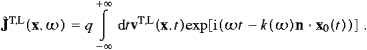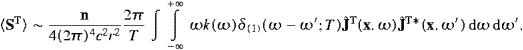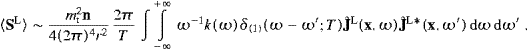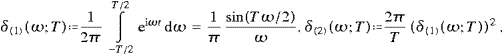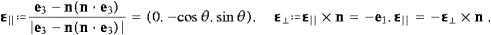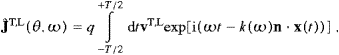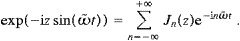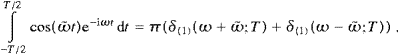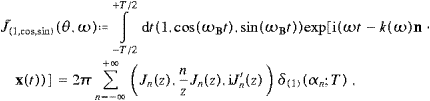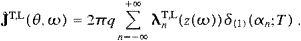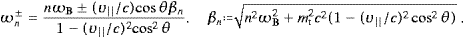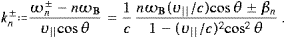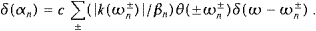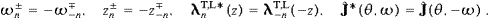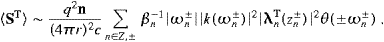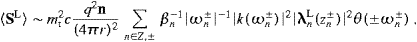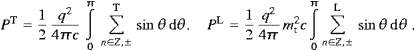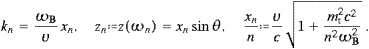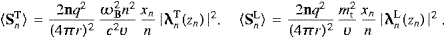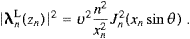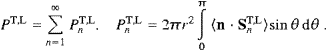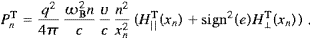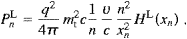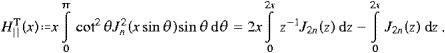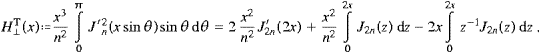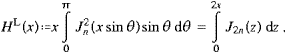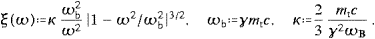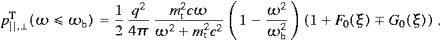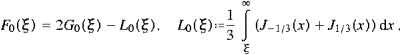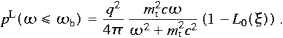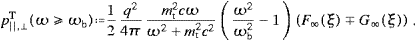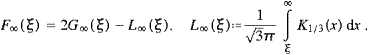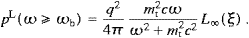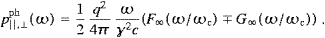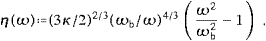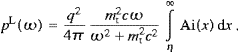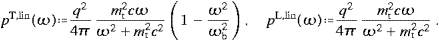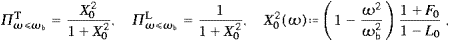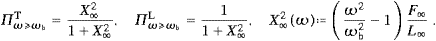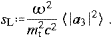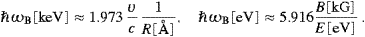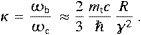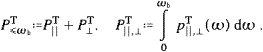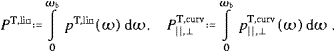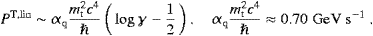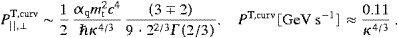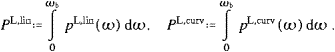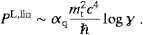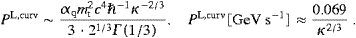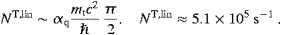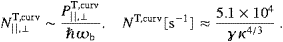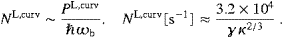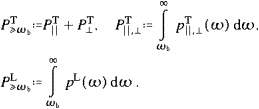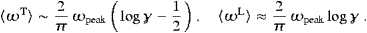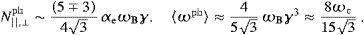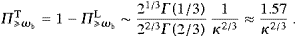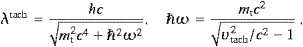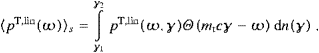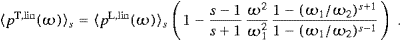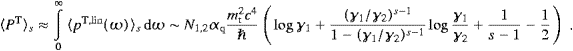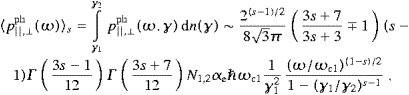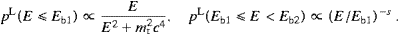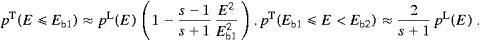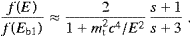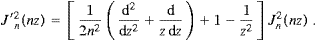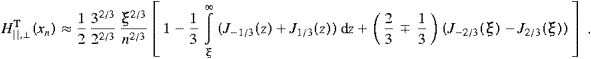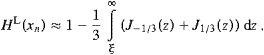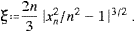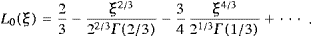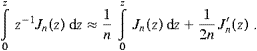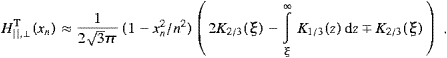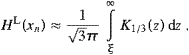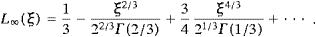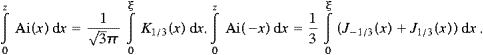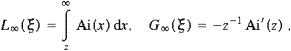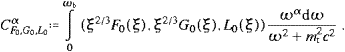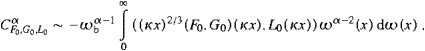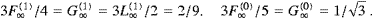Volume 335, Issues 3-4, 15 April 2004, Pages 577-610
Abstract
The emission of superluminal quanta (tachyons) by ultra-relativistic electrons gyrating in magnetic fields is investigated. The tachyonic Liénard–Wiechert potentials of helically orbiting charges are derived, as well as the superluminal energy flux and the transversal and longitudinal spectral densities. We calculate the tachyonic synchrotron power, its angular dependence, the mean energy of the superluminal quanta radiated, tachyonic emission rates, the spectral maxima, critical and break frequencies, and we identify the Stokes parameter of the longitudinal radiation. The tachyonic energy densities are averaged with electronic power-law distributions, and the spectral indices are determined. Quantitative estimates are given for superluminal synchrotron radiation generated in storage rings, the Jovian magnetosphere, and supernova remnants. The spectral density of Jupiter's tachyonic X-ray emission is inferred from radio fluxes obtained from SL9 pre-impact observations and the Cassini fly-by, and we identify the tachyonic spectral peak at 2 keV in the ROSAT and Einstein spectral maps. We scrutinize multiwavelength observations of galactic supernova remnants, pointing out evidence in their wideband spectra for the TeV γ-radiation to be tachyonic rather than a consequence of inverse Compton scattering or pion decay. In the Crab Nebula, the electronic source population generating this radiation extends beyond the ‘knee’ of the cosmic ray spectrum.
Author Keywords: Author Keywords: Superluminal radiation; Curvature radiation; Tachyons; Proca equation; Negative mass-square; Storage rings; Planetary magnetospheres; Van Allen belts; Jupiter's aurora; Supernova remnants; Synchrotron nebulae; Crab Nebula; TeV γ-rays
Article Outline
- 1. Introduction
- 2. Superluminal radiation by helically moving charges
- 3. Tachyonic spectral densities, curvature radiation, and the longitudinal Stokes parameter
- 4. Radiant power, tachyonic number counts, and spectral indices
- 5. Tachyonic X-rays from Jupiter's magnetosphere
- 6. Tachyonic gamma-rays from the shock-heated plasmas of supernova remnants
- Acknowledgements
- Appendix A. Superluminal spectral and power asymptotics
- References
1. Introduction
We will study the spectral densities of superluminal radiation fields generated by ultra-relativistic particles in helical and circular orbits (tachyonic synchrotron radiation). We will discuss examples with orbital radii varying over some 15 orders of magnitude, from storage rings via planetary radiation belts to shell supernova remnants and plerions. Superluminal quanta are a sort of photons with negative mass-square, a quantized Proca field minimally coupled to subluminal matter [1, 2, 3 and 4]. The coupling strength of tachyons to matter is determined by the tachyonic fine structure constant; the ratio of electric and tachyonic fine structure constants is estimated from Lamb shifts in hydrogenic ions, αq/αe≈1.4×10−11, like the tachyon-electron mass ratio, mt/me≈1/238, cf. [5].
Although the Proca equation with negative mass-square is formally close to electromagnetic theory, there are some marked differences such as the third degree of freedom, longitudinally polarized quanta. In the ultra-relativistic limit studied here, the longitudinal radiation is even more pronounced than its transversal counterpart. If tachyons are radiated in the MeV range or above, the tachyon mass is negligible in the dispersion relation, so that they propagate very nearly at the speed of light, and then the longitudinal polarization gets crucial in distinguishing them from photons. At low energies, from soft X-rays down to radio frequencies, the tachyon mass dominates, so that tachyons cannot exceed a wavelength of roughly 6 Å. Low-energy tachyons can thus be discerned from photons by their wavelength, polarization, and speed. A basic difference to Maxwell's theory is the residual radiation in the limit of infinite curvature radius. Particles in linear uniform motion with regard to the cosmic microwave background can radiate superluminal quanta. In the ultra-relativistic limit, the spectrum of this radiation is not sharply peaked, extending over a broad frequency range, from the spectral maximum determined by the tachyon mass up to a break frequency depending on the Lorentz factor of the inertial source [6]. We will consider a finite gyroradius, so that the frequencies radiated extend beyond this break frequency by virtue of curvature radiation, which generates a smooth exponential cutoff in the tachyonic spectral densities.
The existence of superluminal quanta has not been established so far; Lamb shifts in hydrogen-like ions, hyperfine splittings, radiative transitions in Rydberg atoms, and ionization cross-sections provide circumstantial evidence [5]. Here, we will search the Jovian magnetosphere and galactic synchrotron nebulae. As for Jupiter's aurora, thanks to the SL9 comet impact and the Cassini spacecraft encounter, the synchrotron radio flux has been measured at various λ, from 90 to 2 cm, and can be used to piece together the electron density. This in turn allows us to infer the tachyon flux emitted in hard X-rays, as well as the slope and the break frequencies of the high-energy tail of the tachyonic spectral density. The ROSAT and Einstein spectral maps indicate line spectra of highly stripped heavy ions in soft X-rays, but also a third radiation peak at 2 keV, well separated from the line spectra, which will be shown to coincide with the peak of the tachyonic spectral density.
In search of high-energy tachyon radiation, we will study galactic supernova remnants with TeV γ-ray spectra, that is, the Crab, Cas A, the remnant of SN 1006, and RX J1713.7–3946, the latter in connection with the nearby GeV γ-ray source 3EG J1714–3857. We will analyze their broadband spectra, from soft X-rays upwards, the spectral breaks and slopes. We will conclude that the EGRET flux data and, in the case of the Crab, the COMPTEL data in the low MeV region, support the identification of their MeV to TeV γ-ray spectra as tachyonic. We will determine the range and index of the power-law electron density generating the superluminal γ-radiation, and conclude that it is distinct from the electron population emitting the electromagnetic synchrotron radiation in the radio-to-X-ray bands.
In Section 2, we derive the tachyonic flux vectors and the integral energy flux emitted by helically moving charges, the formalism of tachyonic synchrotron and cyclotron radiation, that is. In Section 3, we specialize to charges in circular, ultra-relativistic motion (subluminal, with high Lorentz factors). We perform the asymptotic summation of the multipole expansion of the superluminal radiation field and calculate the transversal and longitudinal spectral densities. In Section 4, we integrate these densities to obtain the power radiated, the tachyonic number counts (emission rates), mean energies, and polarization ratios. We average the superluminal spectral densities with electronic power-law distributions, and relate the power-law index to the tachyonic spectral index. In Section 5, we first give numerical estimates for tachyon radiation in storage rings and compare with electromagnetic synchrotron radiation. We then turn to the Jovian magnetosphere, and infer the slopes of the tachyonic spectral density from the radio electrons. Jupiter's tachyon spectrum extends over the hard and high-energy X-ray bands, and we identify the tachyonic spectral peak in the ROSAT and Einstein spectral maps. In Section 6, we scrutinize galactic supernova remnants with known TeV γ-ray fluxes, and identify tachyonic spectral slopes in their multi-band spectra. The electron density generating the superluminal γ-rays is inferred from the tachyonic break energies and spectral slopes. The conclusions are stated at the end of 5 and 6. In Appendix A, we sketch the stationary phase asymptotics of the tachyonic spectral densities and the power asymptotics.
2. Superluminal radiation by helically moving charges
The superluminal radiation field solves the Proca equation
with negative mass-square, (□+mt2)Aα=−c−1jα,
subjected to the Lorentz condition A,μμ=0.
The sign conventions for metric and d'Alembertian are ημν=diag(−1,1,1,1)
and □ ημν∂μ∂ν,
respectively. The tachyon mass has the dimension of an inverse length,
a shortcut for mtc/
ημν∂μ∂ν,
respectively. The tachyon mass has the dimension of an inverse length,
a shortcut for mtc/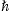 ,
estimated as mt/me≈1/238
from Lamb shifts in hydrogenic systems [5]. We will
mainly work in Fourier space, representing the spatial component of the
vector potential as
,
estimated as mt/me≈1/238
from Lamb shifts in hydrogenic systems [5]. We will
mainly work in Fourier space, representing the spatial component of the
vector potential as
In (2.2), (2.3), (2.4), (2.5), (2.6), (2.7), (2.8), (2.9) and (2.10), we
summarize the classical radiation theory, tachyon radiation by
arbitrarily moving charges [4 and 6]. The Fourier
transform of the current is split into a transversal and longitudinal
component,
We consider the trajectory of a subluminal particle x0(t),
The transversal and longitudinal components of the velocity are vT(x,t)
 v−n(n·v)
and vL(x,t)
v−n(n·v)
and vL(x,t) n(n·v),
respectively, cf. (2.2), so that
transform (2.4) of the
current can be assembled as
n(n·v),
respectively, cf. (2.2), so that
transform (2.4) of the
current can be assembled asThe asymptotic Liénard–Wiechert potentials of the tachyonic charge are thus given by (2.3) with this
and the averaged longitudinal Poynting vector,
with (2.6) substituted. Here, we use a standard limit definition of the Dirac function,
so that δ(1)(ω;T→∞)=δ(ω), and the same for δ(2). The purpose of these limit representations is to avoid ill-defined squares of δ-functions. The radiant power is obtained by integrating the flux through a sphere of radius r→∞,
with the solid angle element dΩ=sin θ dθ d
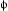 .
.
We specialize to helical motion; the subluminal source moves
with constant speed, otherwise there are no restrictions on the
velocity. The ultra-relativistic limit, tachyonic synchrotron radiation
from particles in circular motion, will be studied in greater detail in
3, 4, 5 and 6. Tachyonic
cyclotron radiation will be dealt with elsewhere; in fact, tachyon
radiation by non-relativistic particles always requires quantization,
cf. the beginning of Section 5. We
consider a constant magnetic field B=(0,0,B),
B>0, and a particle with constant speed υ,
electric charge e and tachyonic charge q.
The equations of motion read d(γmv)/dt=(e/c)v×B,
where γ (1−υ2/c2)−1/2.
Heaviside–Lorentz units are used throughout, and e
is defined negative for electrons. We so find the helix
(1−υ2/c2)−1/2.
Heaviside–Lorentz units are used throughout, and e
is defined negative for electrons. We so find the helix
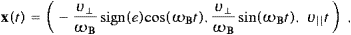
where α is the pitch angle between B and v, and 0<α<π. The gyrofrequency relates to the Larmor frequency as ωL=ωBγ/2. For circular motion in the (x,y)-plane, we have of course α=π/2. We will also admit sign(e)=0 in (2.11), that is, planar transversal oscillations, realizable by undulators in storage rings [7], though we will not discuss this here. The notation is kept close to electromagnetic synchrotron radiation [8, 9, 10 and 11].
We introduce polar coordinates with B
as polar axis and polar angle θ, and consider the wave vector in the (y,z)-plane,
without loss of generality, so that k k(ω)n,
n=(0,sin θ,cos θ), with k(ω)
defined in (2.3). There is
no necessity to specify k(ω) for ω=0, as there is
no wave propagation in this case. The ei
are unit vectors along the coordinate axes, and we define two further
unit vectors,
k(ω)n,
n=(0,sin θ,cos θ), with k(ω)
defined in (2.3). There is
no necessity to specify k(ω) for ω=0, as there is
no wave propagation in this case. The ei
are unit vectors along the coordinate axes, and we define two further
unit vectors,
 ||
and
||
and 
 constitute an orthonormal triad. We may thus write the transversal and
longitudinal components of the velocity as
constitute an orthonormal triad. We may thus write the transversal and
longitudinal components of the velocity as ||(υ||
sin θ−υ
||(υ||
sin θ−υ cos θ cos(ωBt))−
cos θ cos(ωBt))−
 υ
υ sign(e)sin(ωBt)
,
sign(e)sin(ωBt)
,and we also note
When studying electromagnetic synchrotron radiation, it is customary to choose a rest frame where the helical orbit appears circular. A noticeable exception is [10], and we will follow the reasoning there. The introduction of a frame comoving along the helical axis is not useful when studying superluminal radiation, as in such frames longitudinal and transversal modes can appear tangled or even advanced. We will study superluminal radiation in the comoving galaxy frame, locally realized by a Minkowskian frame in which the microwave background is isotropic, that is, Planckian with an isotropic temperature. Both the causality and the energy concept for tachyons are based on the universal cosmic time order, on the absolute space–time defined by the galaxy grid, locally manifested by the background radiations and the cosmic ether [4, 12, 13 and 14]. The helix (2.11) is meant in this frame, in a locally geodesic neighborhood in which the microwave radiation is isotropic.
We start by truncating the integral representation (2.6) of the
current,
To this end, we use the smooth limit representation (2.9) of the δ-function and the truncated Fourier transforms
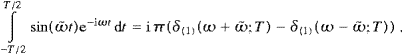
as well as the identities Jn+1−Jn−1=−2Jn′(z) and Jn+1+Jn−1=2(n/z)Jn(z). Expansion (2.16) amounts to a reordered multipole expansion, frequently used in radiation problems with periodically moving sources [11]. In this way, we arrive at
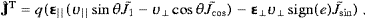
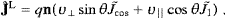
Collecting terms, we may write

 ||(υ||sin
θ−(n/z)υ
||(υ||sin
θ−(n/z)υ cos θ)Jn(z)−i
cos θ)Jn(z)−i
 υ
υ sign(e)Jn′(z)
,
sign(e)Jn′(z)
,As for the flux vectors ((2.7) and (2.8)), we need to know the zeros ωn of αn(ω)=0, cf. (2.19). For every n, there are at most two solutions,
βn
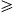 0, and
we define
0, and
we defineApparently, kn+>0 and kn−<0, and thus only positive ωn+ and negative ωn− can be solutions, because only then kn+=k(ωn+) and kn−=k(ωn−), respectively. Hence, for sufficiently large |n|, there is exactly one solution, namely ωn+ for positive n, and ωn− for negative integers. If the mass term is dominant in (2.22), there may be two solutions of αn(ω)=0 or none. Solutions ωn±=0 are discarded, as they do not correspond to wave modes. Hence,
We note J−n(−z)=Jn(z) and J−n′(−z)=−Jn′(z), define
and find the symmetries
With these preparations, we can readily compile the Poynting vectors ((2.7) and (2.8)),
where |λn|2
 λn·λn*.
In ((2.27) and (2.28)), we may
replace ∑n
λn·λn*.
In ((2.27) and (2.28)), we may
replace ∑n Z,± by ∑n=0,±+2
∑n
Z,± by ∑n=0,±+2
∑n 1,±
without further changes, due to symmetries (2.26). In (2.29) we refrain
from writing sign2(e)=1,
since in this way the contributions of the two linear transversal
polarizations (defined by
1,±
without further changes, due to symmetries (2.26). In (2.29) we refrain
from writing sign2(e)=1,
since in this way the contributions of the two linear transversal
polarizations (defined by  ||,
||, in ((2.12) and (2.21))) to the
radiated power can easily be distinguished; the terms stemming from the
in ((2.12) and (2.21))) to the
radiated power can easily be distinguished; the terms stemming from the

 -polarized
component of the radiation field are proportional to sign2(e).
Moreover, by putting sign2(e)=0,
we find the radiation generated by oscillating charges in undulator
fields, mentioned after (2.11). The power
transversally and longitudinally radiated is thus, cf. (2.10),
-polarized
component of the radiation field are proportional to sign2(e).
Moreover, by putting sign2(e)=0,
we find the radiation generated by oscillating charges in undulator
fields, mentioned after (2.11). The power
transversally and longitudinally radiated is thus, cf. (2.10),where the summation signs stand for the series in the flux vectors ((2.27) and (2.28)), respectively. In the next section, we will evaluate these vectors for ultra-relativistic circular motion, and derive explicit formulas for the tachyonic spectral distributions. In Section 4, we will have a closer look at the radiant powers (2.31).
3. Tachyonic spectral densities, curvature radiation, and the longitudinal Stokes parameter
We derive the transversal and longitudinal spectral densities
for tachyon radiation emitted by ultra-relativistic (subluminal)
particles, υ/c≈1, in circular motion. The context is
given in Section 2,
specialized to circular orbits, υ||=0, υ =υ.
The spectral modes are ωn=nωB,
cf. (2.22), so that
in the notation of ((2.19) and (2.23)),
=υ.
The spectral modes are ωn=nωB,
cf. (2.22), so that
in the notation of ((2.19) and (2.23)),
 ST,L
ST,L =∑n=1∞
=∑n=1∞
 SnT,L
SnT,L ,
where
,
where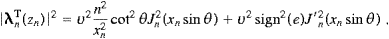
Carrying out the angular integration, we find the transversal and longitudinal components of the total power radiated as
More explicitly,
where the power radiated in the transversal linear
 ||
and
||
and 
 polarizations is determined by
polarizations is determined byrespectively, and the longitudinally radiated power is defined by
cf. Appendix A for further comments on these identities. Radiation generated by transversal planar oscillations corresponds to sign2(e)=0; we will always indicate sign2(e) to distinguish the polarization components of the transversal radiation, cf. after (2.30).
The preceding calculations are exact, apart from the r→∞
asymptotics, which is sufficient to calculate the radiated energy. We
will evaluate PnT,L
for large n and υ/c≈1. This can
be done by means of the Nicolson asymptotics sketched in Appendix A. As n
is large, we may pass to continuous frequencies via ω=nωB,
so that PnT,L
dn≈pT,L(ω)
dω, with the spectral densities
First we consider the case xn/n
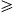 1, which
means frequencies satisfying ω
1, which
means frequencies satisfying ω ωb.
In this regime, the spectral densities follow from ((3.5) and (3.6)), with
substitutions ((A.7) and (A.8)). The
transversal density is assembled as
ωb.
In this regime, the spectral densities follow from ((3.5) and (3.6)), with
substitutions ((A.7) and (A.8)). The
transversal density is assembled aswhere, for ω
 ωb,
ωb,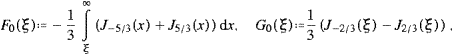
with ξ and ωb in (3.11). The lower plus-sign in (3.13) refers to the
 -polarization.
The longitudinal spectral density reads
-polarization.
The longitudinal spectral density readsThe second case, xn/n 1,
refers to the upper frequency range, ω
1,
refers to the upper frequency range, ω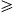 ωb.
Explicit expressions for the spectral densities again follow from ((3.5) and (3.6)), but now
with substitutions ((A.17) and (A.18)). The
transversal density is composed as in (3.12), with
ωb.
Explicit expressions for the spectral densities again follow from ((3.5) and (3.6)), but now
with substitutions ((A.17) and (A.18)). The
transversal density is composed as in (3.12), with
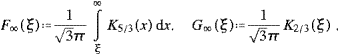
where ξ and ωb are defined in (3.11). Finally, the longitudinal density in this frequency range,
The asymptotic expansions of the spectral functions F0,∞, G0,∞ and L0,∞ are listed in ((A.10), (A.11), (A.19) and (A.20)).
The massless limit is easily recovered, electromagnetic
radiation that is, where ξ reduces to ξmt=0=ω/ωc,
with the critical frequency ωc (3/2)ωBγ3.
As ωb=γmtc→0,
we find from (3.16),
(3/2)ωBγ3.
As ωb=γmtc→0,
we find from (3.16),
Even though densities ((3.13) and (3.16)) have a
very different shape in the upper and lower spectral range, they
smoothly join at ωb, in fact analytically, and
the same holds for the longitudinal densities ((3.15) and (3.18)). To see
this, we define
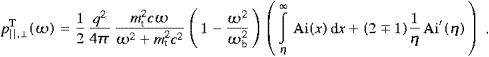
valid throughout the spectral range. The lower plus-sign again refers to the
 -polarization.
In the next section, we will integrate these densities to obtain the
radiant power. This will be done asymptotically, with κ as expansion
parameter, cf. (3.11).
-polarization.
In the next section, we will integrate these densities to obtain the
radiant power. This will be done asymptotically, with κ as expansion
parameter, cf. (3.11).
We return to the lower spectral range, ω ωb,
cf. ((3.13) and (3.15)). In the
limit κ→∞, i.e., for ξ→∞ (at a fixed frequency), the spectral functions
F0, G0
and L0 all vanish, which
happens in the limit of infinite gyroradius, since κ∝R,
as will be shown in (4.2). This
suggests to split the spectral densities into
ωb,
cf. ((3.13) and (3.15)). In the
limit κ→∞, i.e., for ξ→∞ (at a fixed frequency), the spectral functions
F0, G0
and L0 all vanish, which
happens in the limit of infinite gyroradius, since κ∝R,
as will be shown in (4.2). This
suggests to split the spectral densities into
The curvature radiation subtracted in (3.22) reads
where the upper minus-sign in (3.24) refers to p||T,curv. The Lorentz factor of the charge enters in the transversal linear density pT,lin via ωb. It also enters in pL,lin, again by ωb, which is the cutoff frequency for uniform motion. A uniformly moving ultra-relativistic charge can only radiate frequencies ω
 ωb.
The radiation in the upper frequency range, ω
ωb.
The radiation in the upper frequency range, ω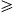 ωb,
is pure curvature radiation, the spectral functions F∞,
G∞ and L∞
vanish in the limit of zero orbital curvature, κ→∞. The densities p||,
ωb,
is pure curvature radiation, the spectral functions F∞,
G∞ and L∞
vanish in the limit of zero orbital curvature, κ→∞. The densities p||, T,L
in (3.22) are
positive definite, but not so the curvature terms pT,curv
and pL,curv in (3.24), which
oscillate for large ξ, cf. (A.11). Densities
(3.21) are
positive throughout the spectral range, of course. In the next section,
we will show that the curvature terms in densities (3.22) give
negative contributions to the radiated power, nearly equal in magnitude
to the power radiated as curvature radiation in the upper frequency
range.
T,L
in (3.22) are
positive definite, but not so the curvature terms pT,curv
and pL,curv in (3.24), which
oscillate for large ξ, cf. (A.11). Densities
(3.21) are
positive throughout the spectral range, of course. In the next section,
we will show that the curvature terms in densities (3.22) give
negative contributions to the radiated power, nearly equal in magnitude
to the power radiated as curvature radiation in the upper frequency
range.
Once the spectral densities are known, the transversal and
longitudinal polarization functions, ΠωT,L pT,L/(pT+pL),
are readily assembled. We find in the lower spectral range,
pT,L/(pT+pL),
are readily assembled. We find in the lower spectral range,
The argument in the spectral functions is always ξ(ω). We will content ourselves with the integrated versions of these ratios, and replace the densities in ΠωT,L by the powers radiated in the respective polarizations, cf. (4.17).
Tachyon radiation can be longitudinally polarized, and the
longitudinal component may even overpower the transversal radiation. I
therefore conclude this section with the Stokes parameter for
longitudinal radiation. Tachyonic E and B-fields
are related to the vector potential in the usual way, by E=(1/c)(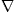 A0−∂A/t)
and B=rot A,
cf. [15]. We consider
a Fourier mode
A0−∂A/t)
and B=rot A,
cf. [15]. We consider
a Fourier mode
 k,1
and
k,1
and  k,2
are real unit vectors (linear polarization vectors) orthogonal to
k,2
are real unit vectors (linear polarization vectors) orthogonal to  k,3
k,3 k0=k/|k|,
so that the
k0=k/|k|,
so that the  k,n
constitute an orthonormal triad. The ak,n
k,n
constitute an orthonormal triad. The ak,n rk,n(t)exp(i
rk,n(t)exp(i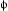 k,n(t))
are complex amplitudes, slowly varying in time as compared to the phase
factor in (3.27). Defining Ek,m
k,n(t))
are complex amplitudes, slowly varying in time as compared to the phase
factor in (3.27). Defining Ek,m
 k,m·Ek,
the polarization can be determined from the time averages
k,m·Ek,
the polarization can be determined from the time averages  Ek,mEk,n*
Ek,mEk,n* ≡
≡ ak,mak,n*
ak,mak,n* taken over the period 2π/ω. In the following we will suppress the
subscript k. The transversal degrees, m,n=1,2,
are settled by the Stokes parametrization
taken over the period 2π/ω. In the following we will suppress the
subscript k. The transversal degrees, m,n=1,2,
are settled by the Stokes parametrization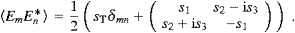

 |a1|2
|a1|2 +
+ |a2|2
|a2|2 , s1
, s1 2
2 |a1|2
|a1|2 −sT=
−sT= r12
r12 −
− r22
r22 ,
,Hence, Tr
 EmEn*
EmEn* =sT,
and
=sT,
and0
 Πtrans
Πtrans 1.
Complete polarization, Πtrans=1, in the
transversal plane is achieved if the ak,n
are time independent, and totally unpolarized radiation, Πtrans=0,
is indicated by vanishing s1,2,3,
so that no direction is preferred in the polarization tensor (3.28). The
parameters sT,1,2,3 account
for the transversal component only, a fifth parameter is needed for the
longitudinal radiation,
1.
Complete polarization, Πtrans=1, in the
transversal plane is achieved if the ak,n
are time independent, and totally unpolarized radiation, Πtrans=0,
is indicated by vanishing s1,2,3,
so that no direction is preferred in the polarization tensor (3.28). The
parameters sT,1,2,3 account
for the transversal component only, a fifth parameter is needed for the
longitudinal radiation,The real tachyonic field strength defined by (3.27) is 2 Re Ek, cf. (2.1); the time averaged (over the period) transversal and longitudinal energy densities of this nearly plane wave are
 ρET
ρET
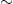 2sT and
2sT and
 ρEL
ρEL
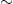 2sL,
respectively [4 and 13]. The
transversal and longitudinal degrees of polarization read accordingly ΠT,L=sT,L/(sT+sL),
which explains the definition of sL.
For instance, we may assume complete polarization in the transversal
plane, Πtrans=1. If two of the amplitudes rn
vanish, we have linear polarization. If one of them vanishes and the
other two are equal in magnitude with a phase difference of ±π/2, the
wave is circularly polarized. The longitudinal component does not show
in the four transversal parameters; a field strength rotating
orthogonally to the transversal plane can still be interpreted as
linear transversal on the basis of sT,1,2,3
only, erroneously, as one ignores the longitudinal energy density. If
the superluminal velocity is close to the speed of light, the tachyon
mass can be neglected in the dispersion relation, cf. (4.22), but
high-energy tachyons can still be discerned from photons by their
longitudinal polarization. In the examples discussed in 5 and 6, the
longitudinal radiation is always more pronounced than the transversal
counterpart. Differential cross sections are perhaps the most practical
means to discriminate longitudinal radiation from transversal tachyons
and photons. Ionization cross sections have been scrutinized to that
effect in [13]. The
polarization of the ionizing radiation affects the angular maxima, the
peaks in the transversal and longitudinal cross sections occur at
different scattering angles.
2sL,
respectively [4 and 13]. The
transversal and longitudinal degrees of polarization read accordingly ΠT,L=sT,L/(sT+sL),
which explains the definition of sL.
For instance, we may assume complete polarization in the transversal
plane, Πtrans=1. If two of the amplitudes rn
vanish, we have linear polarization. If one of them vanishes and the
other two are equal in magnitude with a phase difference of ±π/2, the
wave is circularly polarized. The longitudinal component does not show
in the four transversal parameters; a field strength rotating
orthogonally to the transversal plane can still be interpreted as
linear transversal on the basis of sT,1,2,3
only, erroneously, as one ignores the longitudinal energy density. If
the superluminal velocity is close to the speed of light, the tachyon
mass can be neglected in the dispersion relation, cf. (4.22), but
high-energy tachyons can still be discerned from photons by their
longitudinal polarization. In the examples discussed in 5 and 6, the
longitudinal radiation is always more pronounced than the transversal
counterpart. Differential cross sections are perhaps the most practical
means to discriminate longitudinal radiation from transversal tachyons
and photons. Ionization cross sections have been scrutinized to that
effect in [13]. The
polarization of the ionizing radiation affects the angular maxima, the
peaks in the transversal and longitudinal cross sections occur at
different scattering angles.
4. Radiant power, tachyonic number counts, and spectral indices
We will study the tachyonic power emitted in the three
polarizations, based on the ultra-relativistic spectral densities
derived in the previous section, that is, the transversal densities p||, T(ω)
in ((3.13) and (3.16)), and the
longitudinal pL(ω) in ((3.15) and (3.18)). We will
discuss the integral number counts (tachyons per unit time) in the
respective polarizations, and compare with electromagnetic synchrotron
radiation. Finally, we will discuss tachyonic spectral slopes generated
by averages over electronic source populations.
T(ω)
in ((3.13) and (3.16)), and the
longitudinal pL(ω) in ((3.15) and (3.18)). We will
discuss the integral number counts (tachyons per unit time) in the
respective polarizations, and compare with electromagnetic synchrotron
radiation. Finally, we will discuss tachyonic spectral slopes generated
by averages over electronic source populations.
We start with some estimates concerning the helix (2.11); the
notation summarized or introduced here will also be used in the tables
of Section 5.
Gyroradius and gyrofrequency relate as R=υ/ωB,
where ωB=eB/(γmc),
e>0, so that
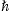 c)=:αe≈1/137
and q2/(4π
c)=:αe≈1/137
and q2/(4π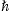 c)=:αq≈1.0×10−13
are the electric and tachyonic fine structure constants. The tachyon
mass mt≈m/238≈2.15
keV/c2 gives a reduced
Compton wave length of
c)=:αq≈1.0×10−13
are the electric and tachyonic fine structure constants. The tachyon
mass mt≈m/238≈2.15
keV/c2 gives a reduced
Compton wave length of 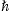 /(mtc)≈0.92
Å; the quotient of tachyonic and electric fine structure constant reads
αq/αe≈1.4×10−11,
all inferred from Lamb shifts in hydrogenic systems [5]. We restore
the natural units, mt→mtc/
/(mtc)≈0.92
Å; the quotient of tachyonic and electric fine structure constant reads
αq/αe≈1.4×10−11,
all inferred from Lamb shifts in hydrogenic systems [5]. We restore
the natural units, mt→mtc/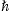 ≈1.09×108
cm−1, cf. the beginning of Section 2, so
that the break frequency reads ωb=γmtc2/
≈1.09×108
cm−1, cf. the beginning of Section 2, so
that the break frequency reads ωb=γmtc2/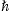 , cf. (3.11). In the
subsequent asymptotics, we will use κ in (3.11) as
expansion parameter, which is the quotient of break frequency and
critical photon frequency, ωc=3ωBγ3/2,
cf. (3.19), relating
to the bending radius as
, cf. (3.11). In the
subsequent asymptotics, we will use κ in (3.11) as
expansion parameter, which is the quotient of break frequency and
critical photon frequency, ωc=3ωBγ3/2,
cf. (3.19), relating
to the bending radius asIn the examples discussed in the following sections, κ will always be large, and the asymptotic expansions will be in κ−2/3, cf. (A.25). The opposite limit, κ→0, can be realized in the surface magnetic fields of pulsars, but we won't consider this here. The peak of the electromagnetic spectral distribution (3.19) is located approximately at 0.286ωc, cf. [16], but the analytically defined ωc is the customary reference value for the location of the bulk of the photon distribution. The tachyonic curvature radiation is peaked at the break frequency ωb, where the linear densities (3.23) terminate, cf. the discussions following ((3.24) and (4.14)).
We turn to the transversal power radiated in the low-frequency
regime, ω ωb=γmtc,
cf. ((3.12), (3.13), (3.14) and (3.15)). This
power can be split into polarization components like the spectral
densities,
ωb=γmtc,
cf. ((3.12), (3.13), (3.14) and (3.15)). This
power can be split into polarization components like the spectral
densities,
 ωbT
into a linear and a curvature component according to ((3.22), (3.23) and (3.24)),
ωbT
into a linear and a curvature component according to ((3.22), (3.23) and (3.24)), ωbT=PT,lin−PT,curv,
PT,curv
ωbT=PT,lin−PT,curv,
PT,curv P||T,curv+P
P||T,curv+P T,curv
,
T,curv
,so that P||,
 T=PT,lin/2−P||,
T=PT,lin/2−P||, T,curv.
The respective number counts such as N
T,curv.
The respective number counts such as N ωbT
are defined in the same way, with the spectral densities divided by
ωbT
are defined in the same way, with the spectral densities divided by 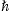 ω. The
power stemming from the linear transversal density reads
ω. The
power stemming from the linear transversal density readswhich is the leading order in the ultra-relativistic 1/γ-expansion of the first integral in (4.4); the second integral gives the transversal curvature radiation in this frequency range,
up to terms of O(κ−2/3), cf. ((A.23), (A.24), (A.25), (A.26) and (A.27)). The lower plus-sign in (4.6) refers to the
 -polarization,
and PT,curv is the total
transversally polarized curvature radiation as defined in (4.4). The linear
power PT,lin in (4.5) is the
residual radiation in the limit of infinite gyroradius; this is the
radiation emitted by an ultra-relativistic charge in uniform motion [6]. The
curvature correction, P||,
-polarization,
and PT,curv is the total
transversally polarized curvature radiation as defined in (4.4). The linear
power PT,lin in (4.5) is the
residual radiation in the limit of infinite gyroradius; this is the
radiation emitted by an ultra-relativistic charge in uniform motion [6]. The
curvature correction, P||, T,curv,
is generated by the F0(ξ)
and G0(ξ)-terms in (3.13), and tends
to reduce the radiation in the low-frequency regime, cf. (4.4) and the
discussion following (3.24).
T,curv,
is generated by the F0(ξ)
and G0(ξ)-terms in (3.13), and tends
to reduce the radiation in the low-frequency regime, cf. (4.4) and the
discussion following (3.24).
The longitudinal radiant power can likewise be decomposed into
a linear and a curvature term,
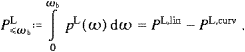
An elementary integration gives the ultra-relativistic linear power,
up to O(γ−1) like in (4.5). The κ−2/3-expansion of the longitudinal curvature radiation can be assembled from ((A.23), (A.24), (A.25), (A.26) and (A.27)). In leading order,
Here and in (4.6), we use 22/3Γ(2/3)≈2.15 and 21/3Γ(1/3)≈3.375.
The transversal low-frequency number counts are defined like
the power components in ((4.3) and (4.4)), with the
integrands divided by 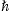 ω. The
transversal count is assembled as N
ω. The
transversal count is assembled as N ωbT=NT,lin−NT,curv,
where NT,curv=N||T,curv+N
ωbT=NT,lin−NT,curv,
where NT,curv=N||T,curv+N T,curv,
and we find
T,curv,
and we find
The longitudinal low-frequency count reads N
 ωbL=NL,lin−NL,curv,
with NL,lin
ωbL=NL,lin−NL,curv,
with NL,lin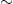 NT,lin,
cf. (4.10), and
NT,lin,
cf. (4.10), andThe κ−2/3-expansion of the powers and count rates beyond the leading order is sketched in ((A.23), (A.24), (A.25), (A.26) and (A.27)).
The high-frequency regime, ω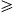 ωb,
is determined by the spectral densities ((3.16), (3.17) and (3.18)) defining
the radiant powers
ωb,
is determined by the spectral densities ((3.16), (3.17) and (3.18)) defining
the radiant powers
 ωbT,L
are defined as in (4.13), with the densities divided by
ωbT,L
are defined as in (4.13), with the densities divided by  ω. The
κ−2/3-expansion of these integrals is outlined
in ((A.28), (A.29), (A.30) and (A.31)), and we
find in leading order,
ω. The
κ−2/3-expansion of these integrals is outlined
in ((A.28), (A.29), (A.30) and (A.31)), and we
find in leading order,where PT,L,curv is the low-frequency curvature radiation calculated in ((4.6) and (4.9)), and NT,L,curv is the corresponding low-frequency count in ((4.11) and (4.12)). This equivalence of high- and low-frequency curvature radiation also persists for the individual transversal polarizations, P||,
 T
T P||,
P||, T,curv,
with P||,
T,curv,
with P||, T
in (4.13) and P||,
T
in (4.13) and P||, T,curv
in (4.6). Relations (4.14) also hold
in next to leading order in the κ−2/3-expansion,
but beyond that the asymptotic series start to differ, as can be seen
by comparing the expansions in ((A.23), (A.24), (A.25), (A.26), (A.27), (A.28), (A.29), (A.30) and (A.31)).
Nevertheless, in leading order this symmetry holds, and it means that
the power radiated in the upper frequency range is more or less drained
from the linear component of the radiation at low frequencies, cf. ((4.4) and (4.7)). The
curvature radiation vanishes for κ→∞ in both regimes; for large κ, the
bulk of the curvature radiation is restricted to a small frequency
range centered at the break frequency ωb,
roughly defined by ξ(ω)
T,curv
in (4.6). Relations (4.14) also hold
in next to leading order in the κ−2/3-expansion,
but beyond that the asymptotic series start to differ, as can be seen
by comparing the expansions in ((A.23), (A.24), (A.25), (A.26), (A.27), (A.28), (A.29), (A.30) and (A.31)).
Nevertheless, in leading order this symmetry holds, and it means that
the power radiated in the upper frequency range is more or less drained
from the linear component of the radiation at low frequencies, cf. ((4.4) and (4.7)). The
curvature radiation vanishes for κ→∞ in both regimes; for large κ, the
bulk of the curvature radiation is restricted to a small frequency
range centered at the break frequency ωb,
roughly defined by ξ(ω) 1, cf. ((3.11), (A.11) and (A.20)). In the
low-frequency regime, the curvature term in the spectral densities is
not exponentially damped but oscillating, so that it averages itself
out when integrated over a frequency range where ξ(ω)
1, cf. ((3.11), (A.11) and (A.20)). In the
low-frequency regime, the curvature term in the spectral densities is
not exponentially damped but oscillating, so that it averages itself
out when integrated over a frequency range where ξ(ω) 1; the asymptotic expansion in ((A.28), (A.29), (A.30) and (A.31)) is based
on that. For large κ, the peak frequency of the spectral distributions (3.22) is ωpeak
1; the asymptotic expansion in ((A.28), (A.29), (A.30) and (A.31)) is based
on that. For large κ, the peak frequency of the spectral distributions (3.22) is ωpeak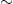 mtc2/
mtc2/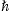 ≈3.27×1018
Hz, determined by the linear densities only, and so are the tachyonic
mean frequencies,
≈3.27×1018
Hz, determined by the linear densities only, and so are the tachyonic
mean frequencies,  ωT,L
ωT,L
 PT,L/NT,L,
PT,L/NT,L,In the tables of Section 5, we will compare tachyonic with electromagnetic synchrotron radiation. To this end, we quote the photonic synchrotron power, Pph=P||ph+P
 ph,
the photon count in the usual linear polarizations, and the photonic
mean energy [11],
ph,
the photon count in the usual linear polarizations, and the photonic
mean energy [11],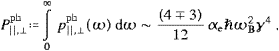
with ωB≈c/R, cf. (4.1). The photon density is defined in (3.19) and integrated in ((A.30) and (A.31)).
Degrees of polarization, ΠT,L PT,L/(PT+PL),
are defined analogously to the polarization functions in ((3.25) and (3.26)), with
the spectral densities replaced by the radiant powers P
PT,L/(PT+PL),
are defined analogously to the polarization functions in ((3.25) and (3.26)), with
the spectral densities replaced by the radiant powers P ωbT,L
or P
ωbT,L
or P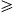 ωbT,L,
ωbT,L,
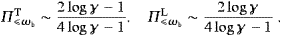
In the low-frequency regime, the linear radiation is much more intense than the curvature radiation, cf. ((4.5), (4.6), (4.7), (4.8) and (4.9)), and the polarization Π
 ωbT,L
is thus determined by the linear powers ((4.5) and (4.8)), for
large κ, that is. In the high-frequency range, the longitudinal
curvature radiation overpowers the transversal one by a factor ∝κ2/3,
cf. ((4.6) and (4.9)), which
shows in Π
ωbT,L
is thus determined by the linear powers ((4.5) and (4.8)), for
large κ, that is. In the high-frequency range, the longitudinal
curvature radiation overpowers the transversal one by a factor ∝κ2/3,
cf. ((4.6) and (4.9)), which
shows in Π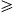 ωbT.
In the transversal plane, we find in both regimes P
ωbT.
In the transversal plane, we find in both regimes P T,curv:P||T,curv
T,curv:P||T,curv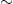 5:1, cf. ((4.6) and (4.14)), as
compared with the photonic ratio P
5:1, cf. ((4.6) and (4.14)), as
compared with the photonic ratio P ph:P||ph=7:1.
ph:P||ph=7:1.
The tables in Section 5 are
compiled with the foregoing formulas; we introduce dimensionless
quantities, E0 E[GeV]
(electron energy), B0
E[GeV]
(electron energy), B0 B[kG],
and R0
B[kG],
and R0 R[m],
so that
R[m],
so that
the tachyonic powers and number counts in ((4.5), (4.6), (4.7), (4.8), (4.9), (4.10), (4.11) and (4.12)) depend on κ and γ only. The critical frequency, the break and peak frequencies, and the corresponding energies scale as
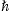 ωc[keV]≈2.22E03R0−1≈6.65×10−2E02B0
.
ωc[keV]≈2.22E03R0−1≈6.65×10−2E02B0
.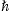 ωb[keV]≈4.21×103E0
,
ωb[keV]≈4.21×103E0
,In the tables of Section 5, we will list ν rather than the circular frequencies used throughout the paper, and the corresponding energies
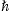 ω will
be denoted by
ω will
be denoted by  b,
b,
 c,
and
c,
and  peak.
The electromagnetic power and the photonic number count, cf. (4.16), scale as
peak.
The electromagnetic power and the photonic number count, cf. (4.16), scale asWave length, energy and speed (group velocity) of a tachyon
relate as [17],
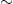 hc/
hc/ b,
cf. (4.20), to be
compared with λComptontach≈5.8
Å (unreduced) and the photonic λcph[Å]≈12.4/
b,
cf. (4.20), to be
compared with λComptontach≈5.8
Å (unreduced) and the photonic λcph[Å]≈12.4/ c[keV].
As for the tachyonic velocity, we find υtach/c−1
c[keV].
As for the tachyonic velocity, we find υtach/c−1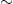 mt2c4/(2
mt2c4/(2 b2)
at the break energy, and a modest υtach/c≈1.41
at the spectral peak. Numerical examples will be given in the tables.
b2)
at the break energy, and a modest υtach/c≈1.41
at the spectral peak. Numerical examples will be given in the tables.
In 5 and 6, we will need
to know how a non-singular electron distribution affects the spectral
densities (3.22). To this
end, we average them with an electronic power-law distribution, dn(γ)∝γ−s
dγ, of index s>1; the electronic Lorentz
factors range in a finite interval, γ1 γ
γ γ2,
the source count reads
γ2,
the source count reads ![]() . In the subsequent sections, we will piece together multi-band spectra
with broken power-laws. A synchrotron model of γ-ray burst spectra with
an analytic cross-over between power-laws is studied in [18 and 19]. A
cross-over from power-law to exponentially damped power-law seems to
apply to the pervading electron density in the Coma Cluster, derived on
the basis of synchrotron and inverse Compton models [20]. Here, we
will content ourselves with broken power-laws; the introduction of
curvature always involves some arbitrariness in the analytic shape of n′(γ),
and tends to make integrations rather clumsy. Like the cosmic ray
spectrum, the wideband spectra of supernova remnants can be assembled
quite convincingly with broken power-laws, cf. Section 6; there
is very little evidence for curvature. The TeV flare spectra of the BL
Lac object Mrk 501 are genuinely curved [21], suggesting
an exponential cutoff factor in dn(γ), possibly with
a further power-law in the exponential [22]. The
averaged linear density (4.23) including
an exponential cutoff is still analytically tractable with incomplete
Γ-functions, but we would not consider blazars here, and broken
power-laws will do for Jupiter's aurora and synchrotron nebulae. We
also restrict ourselves to the linear densities (3.23); the
leading order of the curvature radiation drops out in the averaging
procedure, cf. after (4.24). These
densities are generated by ultra-relativistic particles, so that γ1
. In the subsequent sections, we will piece together multi-band spectra
with broken power-laws. A synchrotron model of γ-ray burst spectra with
an analytic cross-over between power-laws is studied in [18 and 19]. A
cross-over from power-law to exponentially damped power-law seems to
apply to the pervading electron density in the Coma Cluster, derived on
the basis of synchrotron and inverse Compton models [20]. Here, we
will content ourselves with broken power-laws; the introduction of
curvature always involves some arbitrariness in the analytic shape of n′(γ),
and tends to make integrations rather clumsy. Like the cosmic ray
spectrum, the wideband spectra of supernova remnants can be assembled
quite convincingly with broken power-laws, cf. Section 6; there
is very little evidence for curvature. The TeV flare spectra of the BL
Lac object Mrk 501 are genuinely curved [21], suggesting
an exponential cutoff factor in dn(γ), possibly with
a further power-law in the exponential [22]. The
averaged linear density (4.23) including
an exponential cutoff is still analytically tractable with incomplete
Γ-functions, but we would not consider blazars here, and broken
power-laws will do for Jupiter's aurora and synchrotron nebulae. We
also restrict ourselves to the linear densities (3.23); the
leading order of the curvature radiation drops out in the averaging
procedure, cf. after (4.24). These
densities are generated by ultra-relativistic particles, so that γ1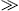 1. The averaging is carried out via
1. The averaging is carried out via
 pL,lin(ω)
pL,lin(ω) s.
The densities pT,lin and pL,lin
are cut off at ωb=mtcγ,
which is accounted for by the step function Θ in (4.23), cf. the
discussion after (3.24). The
longitudinal density pL,lin
depends on the Lorentz factor only via the cutoff frequency ωb.
We thus find the averages,
s.
The densities pT,lin and pL,lin
are cut off at ωb=mtcγ,
which is accounted for by the step function Θ in (4.23), cf. the
discussion after (3.24). The
longitudinal density pL,lin
depends on the Lorentz factor only via the cutoff frequency ωb.
We thus find the averages,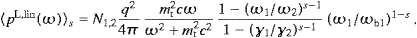
 max(ω,ωb1),
ω2(ω)
max(ω,ωb1),
ω2(ω) max(ω,ωb2),
ωb1,2
max(ω,ωb2),
ωb1,2 mtcγ1,2
,
mtcγ1,2
,Clearly, these densities vanish for ω>ωb2, where ω1/ω2=1. In the high-frequency band, ωb1
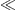 ω
ω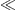 ωb2,
we find
ωb2,
we find  pT,L,lin
pT,L,lin s∝ω−s,
so that the tachyonic spectral index coincides with the electronic
power-law index, in strong contrast to the photon index, cf. (4.26). In the
low-frequency regime, we recover
s∝ω−s,
so that the tachyonic spectral index coincides with the electronic
power-law index, in strong contrast to the photon index, cf. (4.26). In the
low-frequency regime, we recover  pT,L,lin
pT,L,lin s∝ω
for ω
s∝ω
for ω mtc,
the linear frequency scaling of the distributions (3.23), and
mtc,
the linear frequency scaling of the distributions (3.23), and  pT,L,lin
pT,L,lin s∝ω−1
holds for mtc
s∝ω−1
holds for mtc ω
ω ωb1.
The curvature radiation generated by the densities ((3.16), (3.18) and (3.24)) can be
averaged like in (4.23), the
procedure outlined in ((A.23), (A.24), (A.25), (A.26), (A.27), (A.28), (A.29), (A.30) and (A.31)) also
applies here, in particular the same variable transformations can be
used, with ω replaced by ωb in (A.25). In
leading order (large κ), the high- and low-frequency components cancel
each other when integrated with ωb−s
dωb, and the higher orders are overpowered by
the averaged linear densities (4.24) and do not
affect their slopes. The same happens with the integral curvature
radiation stemming from a singular electron distribution, cf. ((4.4), (4.7) and (4.14)).
ωb1.
The curvature radiation generated by the densities ((3.16), (3.18) and (3.24)) can be
averaged like in (4.23), the
procedure outlined in ((A.23), (A.24), (A.25), (A.26), (A.27), (A.28), (A.29), (A.30) and (A.31)) also
applies here, in particular the same variable transformations can be
used, with ω replaced by ωb in (A.25). In
leading order (large κ), the high- and low-frequency components cancel
each other when integrated with ωb−s
dωb, and the higher orders are overpowered by
the averaged linear densities (4.24) and do not
affect their slopes. The same happens with the integral curvature
radiation stemming from a singular electron distribution, cf. ((4.4), (4.7) and (4.14)).
We integrate the averaged densities (4.24) by making
use of γ1 1, to find the averaged transversal power,
1, to find the averaged transversal power,
 PL
PL s,
with −1/2 in the parenthesis dropped. (We have again restored the
units, mt→mtc/
s,
with −1/2 in the parenthesis dropped. (We have again restored the
units, mt→mtc/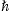 ).
This can also be derived by directly averaging the powers ((4.5) and (4.8)) with dn(γ).
The linear count rates do not depend in leading order on the Lorentz
factor, cf. (4.10), and are
therefore not affected by the averaging, apart from the factor N1,2,
of course. The tachyonic mean frequencies are thus
).
This can also be derived by directly averaging the powers ((4.5) and (4.8)) with dn(γ).
The linear count rates do not depend in leading order on the Lorentz
factor, cf. (4.10), and are
therefore not affected by the averaging, apart from the factor N1,2,
of course. The tachyonic mean frequencies are thus  ωT,L
ωT,L s
s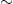 (2/π)ωpeak(log γ1+
(2/π)ωpeak(log γ1+ ),
with the parenthesis completed as in (4.25). This is
to be compared with the mean frequencies (4.15) stemming
from a singular electron distribution.
),
with the parenthesis completed as in (4.25). This is
to be compared with the mean frequencies (4.15) stemming
from a singular electron distribution.
For comparison, we quote the electromagnetic average [11],
 ph(ω,γ)
defined in (3.19) and the
critical photon frequencies ωc1,2 taken at γ1,2.
(The critical frequency scales as ωc∝γ2,
since ωB∝γ−1, cf. ((4.1) and (4.2)).) This is
derived by extending the integration boundaries in (4.26) to zero
and infinity and applying (A.30). The
photon distribution is strongly peaked, more or less at the mean
frequency, cf. (4.16) and after (4.2). The
tachyon densities pT,L,lin
are much more extended, with a mean frequency largely deviating from
the spectral peak at 2.15 keV, cf. (4.15) and Table 2 in Section 5. The
extension of the integration boundaries in (4.26) is only
permissible if ω lies well within the band ωc1
ph(ω,γ)
defined in (3.19) and the
critical photon frequencies ωc1,2 taken at γ1,2.
(The critical frequency scales as ωc∝γ2,
since ωB∝γ−1, cf. ((4.1) and (4.2)).) This is
derived by extending the integration boundaries in (4.26) to zero
and infinity and applying (A.30). The
photon distribution is strongly peaked, more or less at the mean
frequency, cf. (4.16) and after (4.2). The
tachyon densities pT,L,lin
are much more extended, with a mean frequency largely deviating from
the spectral peak at 2.15 keV, cf. (4.15) and Table 2 in Section 5. The
extension of the integration boundaries in (4.26) is only
permissible if ω lies well within the band ωc1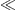 ω
ω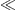 ωc2.
(If the integration boundary in the integrals (A.30) is cut,
they admit antiderivatives in terms of Lommel functions with simple
asymptotic expansions.) It is only in this band that the averaged
photon density has a power-law decay ∝ω−α, with α
ωc2.
(If the integration boundary in the integrals (A.30) is cut,
they admit antiderivatives in terms of Lommel functions with simple
asymptotic expansions.) It is only in this band that the averaged
photon density has a power-law decay ∝ω−α, with α (s−1)/2.
As κ=ωb/ωc is large
throughout the averaging interval, this band noticeably differs from
the tachyonic high-frequency band ωb1
(s−1)/2.
As κ=ωb/ωc is large
throughout the averaging interval, this band noticeably differs from
the tachyonic high-frequency band ωb1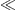 ω
ω ωb2,
where the tachyon densities (4.24) admit a
power-law slope of index s, even though these bands
can overlap.
ωb2,
where the tachyon densities (4.24) admit a
power-law slope of index s, even though these bands
can overlap.
5. Tachyonic X-rays from Jupiter's magnetosphere
A theory of tachyons should provide clues as to where to find them. In Table 1, Table 2, Table 3 and Table 4,we give some estimates to that effect by comparing tachyonic with electromagnetic synchrotron radiation. The examples cover a wide range of electron energies and gyroradii, and a smaller range of magnetic fields. Extremely high magnetic field strengths require different asymptotics, cf. after (4.2), let alone quantum corrections which can completely change the shape of the classical spectral densities by generating a cutoff before the classical spectral peak is reached [11 and 23]. Even for moderate magnetic field strengths, there is a pronounced tachyonic quantum effect emerging in the low-energy cyclotron limit, unparalleled in electromagnetic theory. There is a threshold velocity, a lower bound on the speed of the (always subluminal) source, below which tachyons can only be radiated as curvature radiation [6]. This threshold velocity is without counterpart in the classical radiation theory, and it coincides, most remarkably, with the speed of the Galaxy in the microwave background, υLG/c≈mt/(2m)≈2.10×10−3. Clearly, the ultra-relativistic synchrotron radiation discussed here is not affected by this.
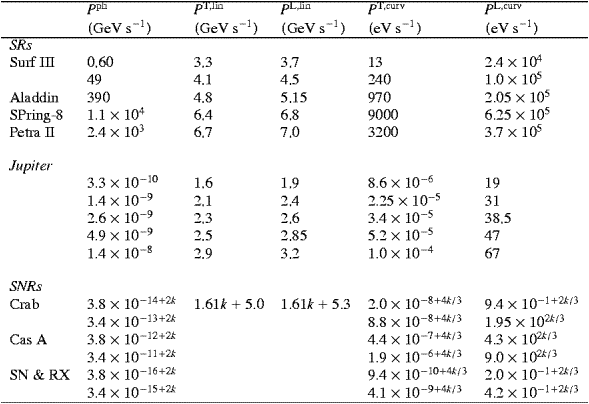
Table 1. Entries as defined in Section 4:
electron energy E (input), electronic Lorentz
factor γ, magnetic field B (input), gyroradius R,
critical photon energy  c,
tachyonic break energy
c,
tachyonic break energy  b,
tachyonic spectral maximum
b,
tachyonic spectral maximum  peak≈2.15
keV. Magnetic field strengths: 100 and 300 μG for the Crab, 1 and 3 mG
for Cas A, 10 and 30 μG for SN 1006. The parameters of SN 1006 apply to
RX J1713.7–3946 as well, and the Crab entries E, γ
and
peak≈2.15
keV. Magnetic field strengths: 100 and 300 μG for the Crab, 1 and 3 mG
for Cas A, 10 and 30 μG for SN 1006. The parameters of SN 1006 apply to
RX J1713.7–3946 as well, and the Crab entries E, γ
and  b
also hold for the other remnants. References for the broadband spectra,
from soft X-rays to TeV γ-rays, are cited in the text. The wave lengths
at 1.4 Jovian radii refer to the photonic spectral peak at λcph/0.286,
cf. Table 2; the
respective radio fluxes [28, 29, 30, 31 and 32] are quoted
in the text. The magnetic field strengths are estimates derived in [34, 35, 36, 42, 44, 51, 55 and 56]. The URLs
(a–d) point to the technical data sheets of the storage rings
b
also hold for the other remnants. References for the broadband spectra,
from soft X-rays to TeV γ-rays, are cited in the text. The wave lengths
at 1.4 Jovian radii refer to the photonic spectral peak at λcph/0.286,
cf. Table 2; the
respective radio fluxes [28, 29, 30, 31 and 32] are quoted
in the text. The magnetic field strengths are estimates derived in [34, 35, 36, 42, 44, 51, 55 and 56]. The URLs
(a–d) point to the technical data sheets of the storage rings
Table 2. Entries as defined in Section 4:
tachyonic mean energy 
 T,L
T,L ,
tachyonic mean frequency
,
tachyonic mean frequency  νT,L
νT,L (transversally and longitudinally radiated), critical photon frequency νc,
tachyonic break frequency νb. Crab entries apply
unless listed otherwise. The continuous parameter k
labels the electron energy, cf. Table 1, one may
envisage 0
(transversally and longitudinally radiated), critical photon frequency νc,
tachyonic break frequency νb. Crab entries apply
unless listed otherwise. The continuous parameter k
labels the electron energy, cf. Table 1, one may
envisage 0 k
k 7 as
typical range, cf. Section 6. The
tachyonic peak frequency, νpeak(1018
Hz)≈0.52, is independent of the electron energy
7 as
typical range, cf. Section 6. The
tachyonic peak frequency, νpeak(1018
Hz)≈0.52, is independent of the electron energy
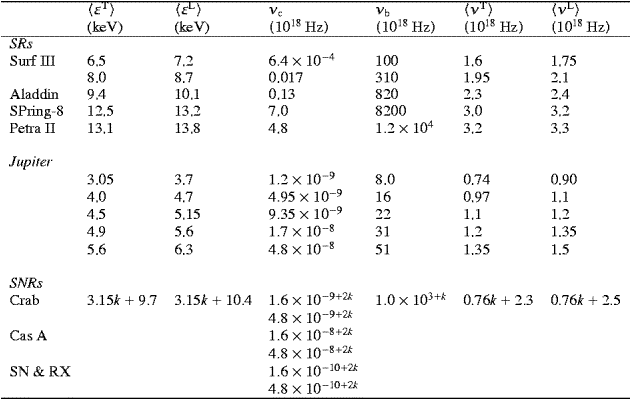
Table 4. Count rates, wave lengths, group velocity, cf. Section 4: unpolarized photon count Nph, polarized tachyon count NT,L,curv (curvature radiation). The ultra-relativistic count rate for the residual radiation (infinite gyroradius) is NT,L,lin≈5.1×105 s−1. Critical photonic wave length λcph, tachyonic wave length at break energy λbtach, group velocity at break energy υtach. To be compared with λpeaktach≈4.1 Å and υtach/c≈1.4 at the spectral maximum at 2.15 keV

A first orientation as to what one can expect is provided by
the storage rings listed in the tables. The frequency peak of the
photonic energy density (3.19) is located at 0.286 c,
very close to the photonic mean energy at 0.308
c,
very close to the photonic mean energy at 0.308 c,
cf. (4.17). This is
in contrast to tachyon radiation, where the peak energy of the
densities (3.23) at 2.15
keV is clearly separated from the mean frequencies
c,
cf. (4.17). This is
in contrast to tachyon radiation, where the peak energy of the
densities (3.23) at 2.15
keV is clearly separated from the mean frequencies 
 T,L
T,L in Table 2. The
photon density is sharply peaked with exponential decay toward higher
frequencies, whereas the linear tachyon densities decay as pT,L,lin∝ω−1
between 2.15 keV and the break energy in the low MeV region. The
tachyonic power radiated as curvature radiation is negligible compared
to the linear power PT,L,lin,
cf. Table 3; this
applies to all examples given in the tables, since the expansion
parameter ωb/ωc (the
ratio of break and critical frequency) is always very large, cf. (4.2). In pulsar
magnetospheres, however, the opposite limit is realized, and then the
curvature radiation dominates; this will be studied elsewhere. In the
ultra-relativistic limit, the power of the linear tachyon radiation
varies only weakly with the electronic Lorentz factor, and it can
easily surpass the photonic power radiated, in Jupiter's case by a
staggering factor of 109. The tachyonic break
energies of the four storage rings range between 0.4 and 50 MeV, as
compared with the tachyonic spectral peak at 2.15 keV; the photonic
spectral peaks of SURF III lie in the near IR and UV, Aladdin's peak
frequency in the extreme UV, and SPring-8 and Petra II radiate hard
X-rays. The tachyonic wavelength at 2.15 keV is 4.1 Å, cf. (4.22), to be
compared with the photonic counterpart λcph/0.286
and the tachyonic wavelengths λbtach
at the break energies in the soft γ-ray band, cf. Table 4. The
photon count Nph of the
storage rings is by three to four orders higher than the tachyonic
emission rate, NT,L,lin≈5.1×105
s−1, cf. Table 4. This
does not seem insurmountable, but it comes on top of the very weak
coupling of tachyons to matter, by a factor of αq/αe≈1.4×10−11
smaller than the electromagnetic interaction, cf. the beginning of Section 4. This
factor shows in ratios of tachyonic and photonic ionization cross
sections and induced transition amplitudes [13 and 15]; in the case
of Petra II, only one in 1014 ionizations is
tachyonic. The chances to detect tachyon radiation in storage rings are
therefore rather slim, even though the longitudinal polarization and
the tachyon speed at the peak frequency can be used as sieves.
in Table 2. The
photon density is sharply peaked with exponential decay toward higher
frequencies, whereas the linear tachyon densities decay as pT,L,lin∝ω−1
between 2.15 keV and the break energy in the low MeV region. The
tachyonic power radiated as curvature radiation is negligible compared
to the linear power PT,L,lin,
cf. Table 3; this
applies to all examples given in the tables, since the expansion
parameter ωb/ωc (the
ratio of break and critical frequency) is always very large, cf. (4.2). In pulsar
magnetospheres, however, the opposite limit is realized, and then the
curvature radiation dominates; this will be studied elsewhere. In the
ultra-relativistic limit, the power of the linear tachyon radiation
varies only weakly with the electronic Lorentz factor, and it can
easily surpass the photonic power radiated, in Jupiter's case by a
staggering factor of 109. The tachyonic break
energies of the four storage rings range between 0.4 and 50 MeV, as
compared with the tachyonic spectral peak at 2.15 keV; the photonic
spectral peaks of SURF III lie in the near IR and UV, Aladdin's peak
frequency in the extreme UV, and SPring-8 and Petra II radiate hard
X-rays. The tachyonic wavelength at 2.15 keV is 4.1 Å, cf. (4.22), to be
compared with the photonic counterpart λcph/0.286
and the tachyonic wavelengths λbtach
at the break energies in the soft γ-ray band, cf. Table 4. The
photon count Nph of the
storage rings is by three to four orders higher than the tachyonic
emission rate, NT,L,lin≈5.1×105
s−1, cf. Table 4. This
does not seem insurmountable, but it comes on top of the very weak
coupling of tachyons to matter, by a factor of αq/αe≈1.4×10−11
smaller than the electromagnetic interaction, cf. the beginning of Section 4. This
factor shows in ratios of tachyonic and photonic ionization cross
sections and induced transition amplitudes [13 and 15]; in the case
of Petra II, only one in 1014 ionizations is
tachyonic. The chances to detect tachyon radiation in storage rings are
therefore rather slim, even though the longitudinal polarization and
the tachyon speed at the peak frequency can be used as sieves.
We turn to Jupiter's radiation belts [24, 25, 26 and 27]. The
non-thermal flux at 90 cm (0.33 GHz or 0.286νc,
cf. Table 1) is 6.2
Jy [28]. At 21 cm
(1.4 GHz), a non-thermal flux of 5.3 Jy is quoted in [29]. At 11 cm
(2.7 GHz) a flux of 4.3 Jy and at 6 cm (5.0 GHz) a non-thermal flux of
3.5 Jy is quoted in [30] and revised
in [31] as stated.
All these fluxes stem from SL9 pre-impact observations. At 2.2 cm (13.8
GHz), a non-thermal flux of 0.42 Jy was observed with Cassini [32]. The
photonic spectral density scales with ν−α when
averaged with an electronic power-law density of index s=2α+1,
cf. after (4.26). In the
90–21 cm range, we thus find the photon index α≈0.1 (as quotient of
log(6.2/5.3) and log(1.4/0.33)), a virtually flat photon spectrum. The
averaged tachyonic spectral densities inherit the electron index as
pointed out after (4.24), and thus
scale with ν−1.2 between the break energies of
33 and 67 keV, cf. Table 1. The
tachyonic mean energies (averaged with the electronic power-law and
Lorentz factors ranging between 15.3 and 31.3, cf. Table 1) are  ωT
ωT s=1.2≈3.5
keV and
s=1.2≈3.5
keV and  ωL
ωL s=1.2≈4.2
keV, as indicated after (4.25). The
electron energies range in the 8–16 MeV interval, with power-law index
1.2. Between the spectral maximum at 2.15 keV and the spectral break at
33 keV, the tachyonic energy density scales with ν−1,
cf. the discussion after (4.24).
s=1.2≈4.2
keV, as indicated after (4.25). The
electron energies range in the 8–16 MeV interval, with power-law index
1.2. Between the spectral maximum at 2.15 keV and the spectral break at
33 keV, the tachyonic energy density scales with ν−1,
cf. the discussion after (4.24).
In the 21–11 cm range, we find α≈0.32, and in the 11–6 cm interval α≈0.33, so that the tachyonic frequency scaling ∝ν−1.6 applies between the break energies of 67 and 130 keV. The 6–2.2 cm interval admits the slopes α≈2 and s≈5, so that the tachyonic spectral densities rapidly decay in the 130–210 keV range, with a steep power-law tantamount to an exponential cutoff. The spectral peak is always located at the tachyon mass, at 2.15 keV, in the ultra-relativistic limit, that is. Hence, tachyon emission from Jupiter's radio electrons should be detectable in hard and high-energy X-rays, throughout the 2–130 keV range. Further SL9 pre-impact fluxes at other wavelengths can be found in [33 and 34], to the same effect.
Soft X-rays from Jupiter's aurora have been detected on two occasions. The ROSAT spectral map [37, 38 and 39] shows three peaks in the number count; the peaks at 0.2 and 0.8 keV are probably due to line emissions from precipitating oxygen and sulfur ions, but there is a third tiny peak located at 2 keV, that has not gained attention so far, coinciding with the peak of the tachyonic spectral densities. This peak also shows in the Einstein map [40]. The ROSAT count rate gets sparse above 0.4 keV, and the Einstein map has only a bandpass of 0.2–3 keV, but the three radiation peaks are clearly discernible in the spectral maps. However, the third peak is too tiny to check for the slope of the differential number count above 2 keV, which should scale with ν−2 in hard X-rays up to the spectral break at 30 keV. It is tempting to identify this peak with tachyon radiation from the radio electrons. Detection of longitudinally polarized X-rays could be the crucial test as to whether the third radiation peak is tachyonic; transversal and longitudinal tachyons are radiated in equal rates and with nearly equal power in Jupiter's magnetosphere, cf. Table 3.
6. Tachyonic gamma-rays from the shock-heated plasmas of supernova remnants
We will identify tachyonic spectral slopes in the broadband
spectra (soft X-ray to TeV γ-ray) of four galactic remnants. We start
by approximating the averaged longitudinal density  pL,lin(ω)
pL,lin(ω) s
in (4.24) by
s
in (4.24) by
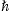 in
both regimes, Eb1,2 denotes
the break energies
in
both regimes, Eb1,2 denotes
the break energies 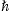 ωb1,2,
and d
ωb1,2,
and d PL
PL s≈pL(E)
dE, cf. (4.25). This
holds for E/Eb2
s≈pL(E)
dE, cf. (4.25). This
holds for E/Eb2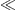 1,
implying γ1/γ2
1,
implying γ1/γ2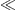 1.
In the same approximation, we write the transversal density
1.
In the same approximation, we write the transversal density  pT,lin(ω)
pT,lin(ω) s
in (4.24) as
s
in (4.24) asWe will consider unpolarized radiation, that is, the density p(E)=pT+pL. The differential energy flux is thus S′(E)=p(E)/(4πd2), where d is the distance to the remnant. This distance and the proportionality factor in (6.1) will drop out in the subsequent ratios. The differential number count, N′(E), relates to the energy flux via dS(E)=E dN(E), of course. The following discussion is based on the rescaled flux density f(E)
 E2N′(E).
We find, by assembling ((6.1) and (6.2)),
E2N′(E).
We find, by assembling ((6.1) and (6.2)),provided mtc2
 E
E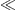 Eb1.
We will consider energies much larger than the tachyon mass, so that
this ratio is constant for E
Eb1.
We will consider energies much larger than the tachyon mass, so that
this ratio is constant for E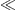 Eb1
and scales as f(E)/f(Eb1)≈(E/Eb1)1−s
for Eb1
Eb1
and scales as f(E)/f(Eb1)≈(E/Eb1)1−s
for Eb1 E
E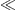 Eb2.
The tachyonic energy density p(E)
attains its maximum at the tachyon mass, and f(E)
stays nearly constant between break energy and maximum. The tachyonic
spectral index s coincides with the electron index
and typically ranges in 1<s<2, in the
X- and γ-ray bands.
Eb2.
The tachyonic energy density p(E)
attains its maximum at the tachyon mass, and f(E)
stays nearly constant between break energy and maximum. The tachyonic
spectral index s coincides with the electron index
and typically ranges in 1<s<2, in the
X- and γ-ray bands.
TeV γ-rays from the Crab have been detected in the 0.5–50 TeV range. A differential flux of N′(E)≈2.79×10−11(E/1 TeV)−2.59 cm−2 s−1 TeV−1 in the 1–20 TeV interval is quoted by the HEGRA Collab. [41]. A recent power-law of the Whipple Group with amplitude 3.12×10−11 and exponent 2.57 applies in the 0.5–8 TeV range [42]. The CANGAROO count [43] extends from 7 to 50 TeV, with amplitude 2.76×10−11 and exponent 2.53. The subsequent calculations are based on NTeV′(E)≈2.9×10−11(E/1 TeV)−2.6 and Eb1≈0.6 TeV. Above this break energy, the tachyonic spectral index s≈1.6 applies, as defined after (4.24). We write fTeV(E)=E2NTeV′(E), so that fTeV(Eb1)≈44.5 eV cm−2 s−1, and infer from (6.3) that fTeV(E) cuts as a plateau horizontally through the error bars of four EGRET points and one COS-B point located in the 1–30 GeV range [42 and 44]. This fTeV-plateau also hits a CELESTE point at 60 GeV [45]. The remaining EGRET flux points below 1 GeV define a power-law slope [46], NMeV′(E)≈9.1×10−9(E/118 MeV)−2.9 cm−2 s−1 MeV−1. There are some contaminated data points in this fit, it is feasible that the slope is slightly flatter, especially if one includes two COS-B points below 0.5 GeV, cf. [44], but not by much. Anyway, we will use s≈1.9 as tachyonic spectral index in this range. The slope fMeV(E)=E2NMeV′(E) joins the GeV plateau at E1≈380 MeV, where fTeV(E1)=fMeV(E1). Hence, fTeV(E) applies above 380 MeV, up to at least 50 TeV. Below 380 MeV, the slope fMeV(E) intersects a second plateau value defined by the COMPTEL data points, which give Nctel′(E)≈1.9×10−4(E/2.6 MeV)−2.0 cm−2 s−1 MeV−1 for the unpulsed flux in the 1–10 MeV range [47 and 48]. This plateau is reproduced by fMeV(E), extended below the spectral break at Eb1≈11 MeV according to (6.3). The break energy is obtained by solving Eb12Nctel′(Eb1)≈1.18fMeV(Eb1); we find Eb12Nctel′(Eb1)≈1.3 keV cm−2 s−1. Finally, most of the keV range is covered by a broken power-law derived from HEAO 1 and earlier observations [49];NX′(E)≈9.23(E/1 keV)−2.13 cm−2 s−1 keV−1 (unpulsed) applies from 17 keV up to the spectral break at 150 keV, and NkeV′(E)≈2.14×10−4(E/150 keV)−2.54 cm−2 s−1 keV−1 holds above 150 keV. The slope E2NX′(E) can be continued with broken power-laws to soft X-ray energies and into the UV, optical, IR and radio bands as done in [50]. The high-energy slope E2NkeV′(E) hits the COMPTEL plateau at E≈1.7 MeV.
The spectrum up to 1.7 MeV is photonic, but the COMPTEL plateau from 1.7 to 11 MeV and the subsequent EGRET slope from 11 to 380 MeV is unlikely to be of electromagnetic origin. A power-law slope preceded by a plateau value of f(E) is characteristic for tachyon radiation. For this reason, I also suggest that the EGRET plateau from 380 MeV to 0.6 TeV and the subsequent power-law slope up to 50 TeV is tachyonic. The EGRET points give a clear picture of the GeV γ-ray spectrum, though they have been criticized on the grounds of contamination and large error bars, as they fail to provide evidence for inverse Compton scattering and pion decay, for the downward slope in the GeV region that is, in all remnants investigated. Plots of the multi-band spectrum with the mentioned flux points can be found in [42, 44, 45, 47 and 48].
The energy range of the electrons producing the tachyonic
spectral slopes and plateaus can be read off from the tachyonic break
energies  b
in Table 1. The
tachyonic slope in the 0.6–50 TeV interval corresponds to 5.15
b
in Table 1. The
tachyonic slope in the 0.6–50 TeV interval corresponds to 5.15 k
k 7.1,
from which we infer electron energies between 0.14 and 13 PeV. The
electronic power-law index coincides with the tachyonic spectral index
of 1.6. The exponent k parametrizes the electron
energy in Table 1. This is
to be compared to the ‘knee’ of the cosmic ray spectrum at k≈6.5
(≈3 PeV) [52]. The second
tachyonic slope, between 11 and 380 MeV, corresponds to 0.42
7.1,
from which we infer electron energies between 0.14 and 13 PeV. The
electronic power-law index coincides with the tachyonic spectral index
of 1.6. The exponent k parametrizes the electron
energy in Table 1. This is
to be compared to the ‘knee’ of the cosmic ray spectrum at k≈6.5
(≈3 PeV) [52]. The second
tachyonic slope, between 11 and 380 MeV, corresponds to 0.42 k
k 1.96,
which translates into electron energies from 2.6 to 91 GeV with index
1.9.
1.96,
which translates into electron energies from 2.6 to 91 GeV with index
1.9.
We turn to the remnant Cas A; γ-rays have been detected in the
1–10 TeV range, with an integral flux of 5.8×10−13
cm−2 s−1 and a slope NTeV′(E)∝(E/1
TeV)−2.5 (HEGRA Collab. [53]), from which
we infer a proportionality constant of 9.0×10−13
cm−2 s−1 TeV−1.
At the break energy Eb1≈1
TeV, we thus find fTeV(Eb1)≈0.90
eV cm−2 s−1, which
extends as plateau fTeV(E)≈1.0
eV cm−2 s−1 into the GeV
and MeV range according to (6.3) (with s≈1.5).
As for the X-ray slopes [54], the
interval 1–120 keV is covered by a broken power-law with spectral break
at 16 keV. The differential number count NX′(E)≈0.038(E/1
keV)−1.8 cm−2 s−1
keV−1 applies below 16 keV, and above it
steepens to NkeV′(E)≈2.6×10−4
(E/16 keV)−3.0 cm−2
s−1 keV−1. The E2NkeV′(E)
slope of the photonic high-energy X-ray tail joins the tachyonic fTeV(E)-plateau
at E≈1.1 MeV, provided that the X-ray count NkeV′(E)
extends as unbroken power-law to this energy. The tachyon spectrum
spreads from 1.1 MeV to 1 TeV with a flat fTeV(E),
and continues above the spectral break at 1 TeV with a slope fTeV(E)≈0.90(E/1
TeV)−0.5 eV cm−2 s−1,
cf. after (6.3). The energy
of the electrons producing this fTeV(E)
can be inferred from the tachyonic break energies  b
in Table 1, like
for the Crab above. The tachyonic 1–10 TeV range corresponds to 5.38
b
in Table 1, like
for the Crab above. The tachyonic 1–10 TeV range corresponds to 5.38 k
k 6.38,
resulting in electron energies of 0.24–2.4 PeV, with a power-law index
of 1.5.
6.38,
resulting in electron energies of 0.24–2.4 PeV, with a power-law index
of 1.5.
As for the remnant SN 1006, an integral X-ray flux of 89 eV cm−2 s−1 in the 0.1–2.0 keV range is quoted in [56], and the differential number count between 0.1 and 1.85 keV scales as NSX′(E)≈0.027(E/1 keV)−2.1 cm−2 s−1 keV−1. Above the spectral break at 1.85 keV, up to 17 keV, the flux scales as NHX′(E)≈0.047(E/1 keV)−3.0 cm−2 s−1 keV−1, cf. [56 and 57]. The observed γ-ray spectrum extends to about 20 TeV (CANGAROO Collab. [58 and 59]), the spectral index is as yet not well determined. fTeV(E) is nearly flat between 1 and 5 TeV, indicating a spectral index s≈1, so that in this range NTeV′(E)≈9×10−12(E/1 TeV)−2 cm−2 s−1 TeV−1. We thus infer fTeV(E)≈9 eV cm−2 s−1 below 5 TeV, and this plateau extends down to 1 GeV, cutting through the EGRET upper limits in the 1–10 GeV range; a plot of the broadband spectrum with the EGRET flux can be found in [59]. The EGRET data indicate a spectral break at 1 GeV and a downward slope ranging from about 50 MeV to 1 GeV. Below 50 MeV, down to high-energy X-rays, there are no flux data available yet. In any case, the fTeV-plateau in the GeV range followed by a spectral break in the low TeV region is also present in this remnant, like in Cas A and the Crab, though the evidence is scantier.
The fourth remnant detected in TeV γ-rays is RX J1713.7–3946; the CANGAROO differential flux is NTeV′(E)≈1.6×10−11(E/1TeV)−2.8 cm−2 s−1 TeV−1 in the 0.4–8 TeV range [60]. We find fTeV(Eb1)≈19 eV cm−2 s−1 at the break energy of 0.8 TeV, followed by the plateau fTeV(E)≈22 eV cm−2 s−1 in the GeV region, cf. (6.3) (with s≈1.8). This plateau cuts horizontally through the data points of the unidentified γ-ray source 3EG J1714–3857 located in the range 0.5–10 GeV. The EGRET spectrum is flat in this region, but starts to steepen below 500 MeV indicating a spectral break, cf. the Crab. A plot of the EGRET points in the wideband spectrum can be found in [61]. The spectrum from 10 MeV down to hard X-rays has not been measured yet. In the 0.5–10 keV interval, the photonic energy flux scales as ENX′(E)∝(E/1 keV)−1.4, and the integral flux in this range is 0.10 keV cm−2 s−1, so that E2NX′(E)≈0.043(E/1 keV)−0.4 keV cm−2 s−1, as inferred from ASCA & ROSAT data [62 and 63]. RXTE observations indicate a steepening of this slope in the 10–30 keV range [64]. The RXTE count does not smoothly join the ROSAT count, there is a discontinuity at 2 keV extending over one order in the count rate. This could be due to background radiation from the Galactic Ridge, but there can also be a tachyonic f(E)-plateau extending down to the tachyon mass at 2.15 keV, cf. (6.3), which is not to be subtracted as background radiation.
Tachyonic γ-rays in the 0.8–8 TeV range correspond to electron
energies from 0.2 to 2 PeV, parametrized by 5.3 k
k 6.3 in Table 1. The fTeV-plateau
in the GeV range cutting through the 3EG J1714–3857 flux points again
suggests that the GeV and TeV radiation is tachyonic; such an extended
plateau is unlikely to be produced by inverse Compton scattering or π0
decay. The TeV γ-ray flux of this remnant is quite on the Crab scale,
whereas the X-ray flux is much weaker and comparable with Cas A, whose
TeV radiation is by one order weaker. TeV γ-rays from other remnants
such as IC 443 and Tycho have escaped detection. This suggests that
there are two energetically different electron populations in remnants
with TeV spectra, one emitting tachyonic MeV to TeV γ-rays, the other
generating the photonic synchrotron radiation in the radio-to-X-ray
bands. I also note that the tachyonic spectral densities in ((6.1) and (6.2)) stem from
the linear densities (4.24), in
particular the rescaled flux density f(E),
key to the preceding discussion, is independent of the magnetic field;
the tachyonic curvature radiation is negligible for the low magnetic
field strengths in the remnants, cf. Table 3 and Table 4.
6.3 in Table 1. The fTeV-plateau
in the GeV range cutting through the 3EG J1714–3857 flux points again
suggests that the GeV and TeV radiation is tachyonic; such an extended
plateau is unlikely to be produced by inverse Compton scattering or π0
decay. The TeV γ-ray flux of this remnant is quite on the Crab scale,
whereas the X-ray flux is much weaker and comparable with Cas A, whose
TeV radiation is by one order weaker. TeV γ-rays from other remnants
such as IC 443 and Tycho have escaped detection. This suggests that
there are two energetically different electron populations in remnants
with TeV spectra, one emitting tachyonic MeV to TeV γ-rays, the other
generating the photonic synchrotron radiation in the radio-to-X-ray
bands. I also note that the tachyonic spectral densities in ((6.1) and (6.2)) stem from
the linear densities (4.24), in
particular the rescaled flux density f(E),
key to the preceding discussion, is independent of the magnetic field;
the tachyonic curvature radiation is negligible for the low magnetic
field strengths in the remnants, cf. Table 3 and Table 4.
The tachyonic luminosity and magnetospheric electron
population of γ-ray pulsars can be inferred from COMPTEL and EGRET
observations. Due to the strong surface fields, the electromagnetic
synchrotron radiation in the γ-ray band is suppressed by a quantum
cutoff, but not so tachyonic γ-radiation. This provides an exceptional
opportunity to search for tachyon radiation, unspoiled by
electromagnetic emission. However, the asymptotics developed here, ωc/ωb 1,
cf. (4.2) and Table 1, does
not apply to excessive magnetic field strengths, the opposite limit is
realized in the surface fields of γ-ray pulsars.
1,
cf. (4.2) and Table 1, does
not apply to excessive magnetic field strengths, the opposite limit is
realized in the surface fields of γ-ray pulsars.
Very promising sources of superluminal γ-rays are TeV blazars; multi-band spectra of Mrk 421 and Mrk 501 are compiled in [21, 65, 66, 67 and 68]. The EGRET flux points, however, do not stem from the specific flares for which the broadband spectra are assembled, and there are also rather large variations in the amplitudes and exponents of the TeV γ-ray fluxes, let alone spectral curvature and cutoff energies. The tachyonic interpretation of the γ-ray spectra again hinges on the GeV radiation, which is not known for the individual flares, although the EGRET points in the spectral maps are quite suggestive to that effect. Finally, tachyons do not interact with IR background photons, so that there is no absorption of tachyonic TeV γ-rays from extragalactic sources by electron–positron creation.
Acknowledgements
The author acknowledges the support of the Japan Society for the Promotion of Science. The hospitality and stimulating atmosphere of the Centre for Nonlinear Dynamics, Bharathidasan University, Trichy, the Institute of Mathematical Sciences, Madras, and the Tata Institute of Fundamental Research, Bombay, are likewise gratefully acknowledged.
References
Appendix A. Superluminal spectral and power asymptotics
We start with the stationary phase asymptotics employed in Section 3. The
Schott identities ((3.7), (3.8) and (3.9)) are a
convenient way of rewriting the powers in the multipole expansion (3.4), and the
notation customary in synchrotron radiation theory is based on them [8 and 11]. These
identities can be derived by using the power series expansion of Jn2
and term by term integration; the J′n2
integration is settled by
The asymptotics of electromagnetic synchrotron radiation
theory also applies to tachyon radiation. Contrary to the photonic
case, however, we have to consider two asymptotic regimes, since xn/n
in (3.1) can be
larger or smaller than one. The Bessel functions in ((3.7), (3.8) and (3.9)) are
replaced by their Nicolson asymptotics, which applies for large
positive n and z, so that z/n≈1,
cf. [69]. If z>n,
in leading order of a 1/n and z/n−1 double series expansion. We also note
In the powers ((3.5) and (3.6)), we can thus approximate, if xn/n
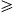 1, cf. (3.1),
1, cf. (3.1),In (A.7), the lower plus-sign refers to the
 -subscript.
In this way, we arrive at the spectral densities ((3.13) and (3.15)) of the
low-frequency regime. The relation F0=2G0−L0
between the spectral functions (3.14) is
obtained by integrating the third identity in (A.6). We note the
expansions
-subscript.
In this way, we arrive at the spectral densities ((3.13) and (3.15)) of the
low-frequency regime. The relation F0=2G0−L0
between the spectral functions (3.14) is
obtained by integrating the third identity in (A.6). We note the
expansions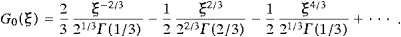
where
A very different asymptotics applies for z<n, familiar from electromagnetic synchrotron radiation theory [11],
This is again the leading order in a 1/n and 1−z/n expansion. (A.13) and (A.14) follow from (A.12) and the identities
To derive the asymptotics in ((A.5) and (A.15)), we use the identity Jn/z=(1/(2n))(Jn+1+Jn−1) and write, within the accuracy of ((A.2) and (A.12)), Jn+k(z)≈Jn(z(1−k/n)), so that ((A.5) and (A.15)) follow by expanding to second order in k/n. One can check by differentiation that these formulas are valid up to terms of O((z/n−1)2).
Hence, if xn/n 1, cf. (3.1), we
approximate the powers ((3.5) and (3.6)) by
1, cf. (3.1), we
approximate the powers ((3.5) and (3.6)) by
with ξ as in (A.9). In (A.17), the lower plus-sign again refers to the
 -subscript,
and we thus recover the spectral densities ((3.16) and (3.18)) of the
high-frequency regime. The relation F∞=2G∞−L∞
between the spectral functions (3.17) follows by
integrating the third identity in (A.16). These
functions admit the expansions
-subscript,
and we thus recover the spectral densities ((3.16) and (3.18)) of the
high-frequency regime. The relation F∞=2G∞−L∞
between the spectral functions (3.17) follows by
integrating the third identity in (A.16). These
functions admit the expansions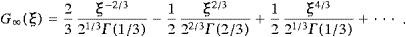
and rapidly decay for ξ→∞,
The representation of the spectral densities by Airy
functions, cf. (3.21),
demonstrates analyticity at the break frequency ωb.
To derive this, we write ξ=(2/3)z3/2,
so that the Airy integral and its (anti-)derivatives read [70 and 71],
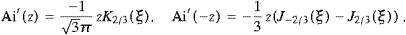
all entire functions, and Ai″(z)=z Ai(z). The integration boundaries may be replaced by
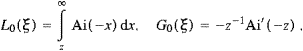
where z=(3ξ/2)2/3. (By the way, Ai′(−z) is the derivative of Ai(z) taken at −z.) The expansions ((A.10) and (A.19)) follow from those of the (anti-)derivatives of Ai(±z), listed in [71]. By substituting (A.22) into the transversal densities ((3.13) and (3.16)), we easily see that they are the analytic ω-continuation of each other, cf. ((3.20) and (3.21)). Similarly, the longitudinal densities ((3.15) and (3.18)) define the same analytic function, determining their high/low-frequency counterpart by analytic continuation.
We turn to the frequency integration of the spectral densities
((3.13) and (3.15)). The
power radiated as curvature radiation in the low-frequency regime, cf. ((4.4) and (4.7)), and the
corresponding number counts can be assembled from the integrals
up to terms of O(γ−2). The parameter κ is defined in (3.11); we need the κ→∞ asymptotics of these integrals, cf. the discussion following (4.2). To this end, we expand in (A.24),
 (1/2)x2/3+(5/24)x4/3
(1/2)x2/3+(5/24)x4/3 (1/16)x2+
(1/16)x2+ ,
,Only the upper signs are relevant at this point, the lower ones will be used in (A.29). The asymptotic expansion of integrals (A.24) is thus effected by (A.25) combined with the Bessel integrals [69],
in analytic continuation. Hence,
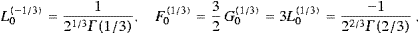
L0(−1/3) is calculated from (A.26) by means of an
 -regularizer,
μ=−1/3+
-regularizer,
μ=−1/3+ .
The use of expansion (A.25) over the
whole integration range, the interchange of summation and integration,
and the analytic continuation in μ can be justified as follows. We
split the integration range in (A.24) into two
intervals, [0,δ] and [δ,∞], where the cut δ lies within the convergence
radius of (A.25). In the lower range, the integrals (A.24) can be
reduced, by means of (A.25), to integrals of type
.
The use of expansion (A.25) over the
whole integration range, the interchange of summation and integration,
and the analytic continuation in μ can be justified as follows. We
split the integration range in (A.24) into two
intervals, [0,δ] and [δ,∞], where the cut δ lies within the convergence
radius of (A.25). In the lower range, the integrals (A.24) can be
reduced, by means of (A.25), to integrals of type 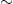 x−1/2.
Collecting terms, we find the expansion indicated in ((A.24), (A.25) and (A.26)).
x−1/2.
Collecting terms, we find the expansion indicated in ((A.24), (A.25) and (A.26)).
The expansion of the radiant powers in the high-frequency
regime, cf. (4.13), is
settled analogously. The integration of the transversal and
longitudinal spectral densities ((3.16) and (3.18)) requires
integrals of type
and substitute expansion (A.25) with the lower signs. The use of this expansion beyond its convergence radius is justified by Watson's Lemma [72], because of the exponential decay of the integrands, cf. (A.20); we have ω(x→∞)
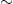 x in this case. A partial
integration with regard to F∞
and L∞ gives
x in this case. A partial
integration with regard to F∞
and L∞ givesto be compared with (A.27),
L∞(−1/3) is obtained by
 -expansion
of the first Γ-function, otherwise there is no analytic continuation
necessary in (A.30). The
asymptotic expansion of integrals (A.28) is thus
obtained by substituting (A.25) (with
lower signs) into (A.29), followed
by an interchange of summation and integration, and a subsequent
application of (A.30). The
curvature radiation, that is, the radiated powers and the number counts
discussed in Section 4, can
be assembled from integrals ((A.23) and (A.28)).
-expansion
of the first Γ-function, otherwise there is no analytic continuation
necessary in (A.30). The
asymptotic expansion of integrals (A.28) is thus
obtained by substituting (A.25) (with
lower signs) into (A.29), followed
by an interchange of summation and integration, and a subsequent
application of (A.30). The
curvature radiation, that is, the radiated powers and the number counts
discussed in Section 4, can
be assembled from integrals ((A.23) and (A.28)).