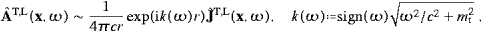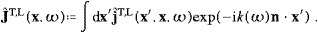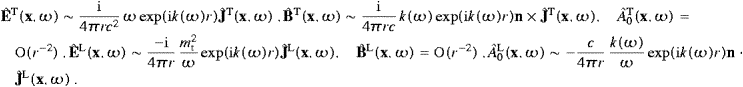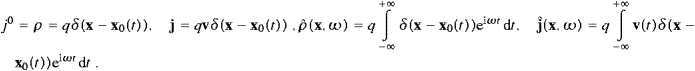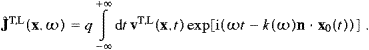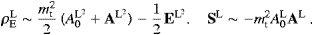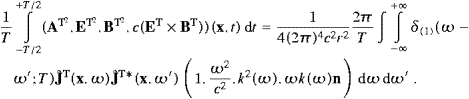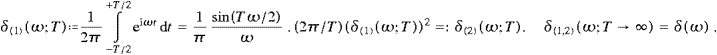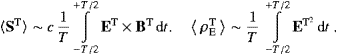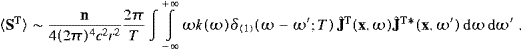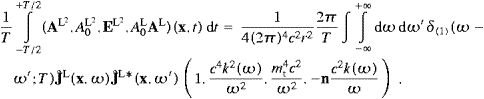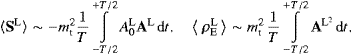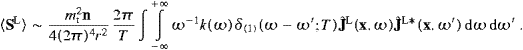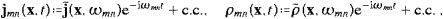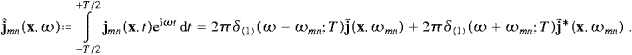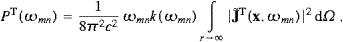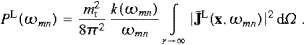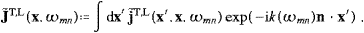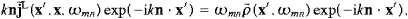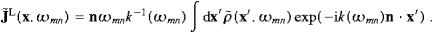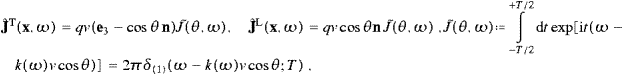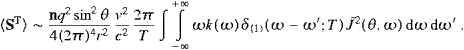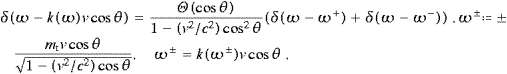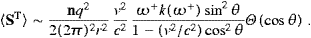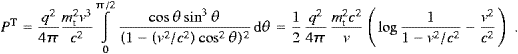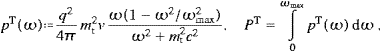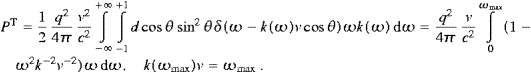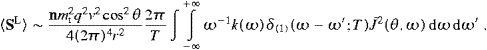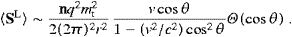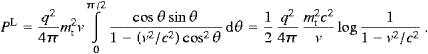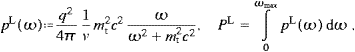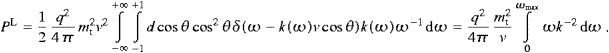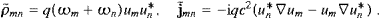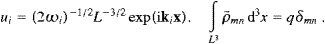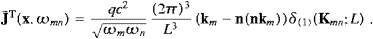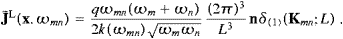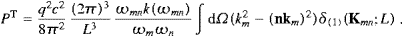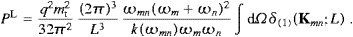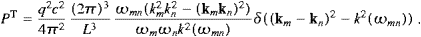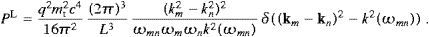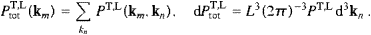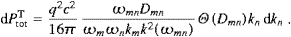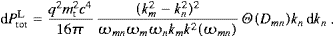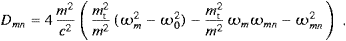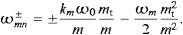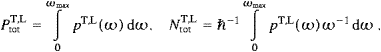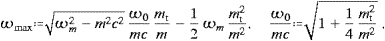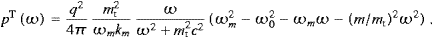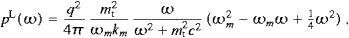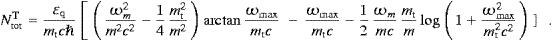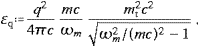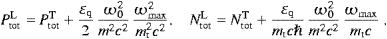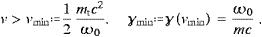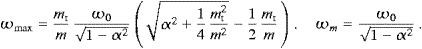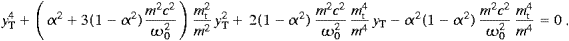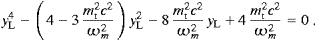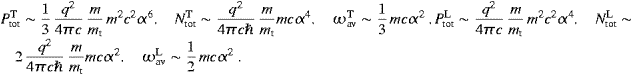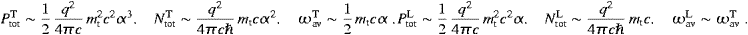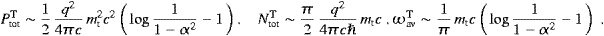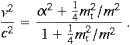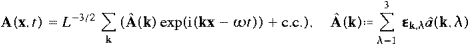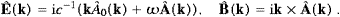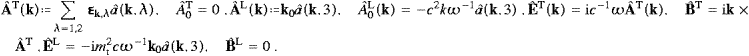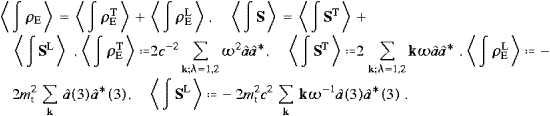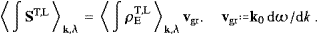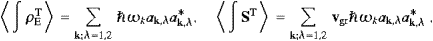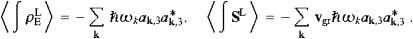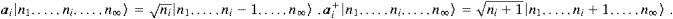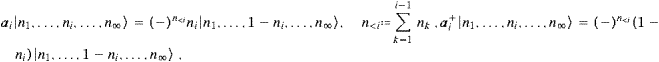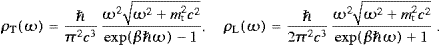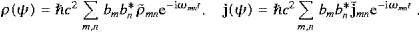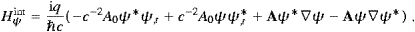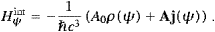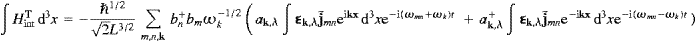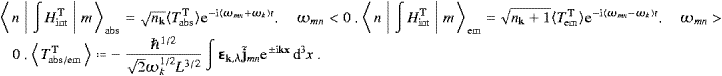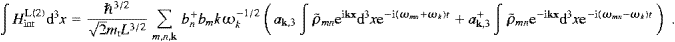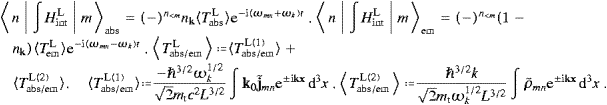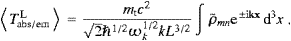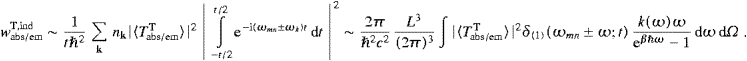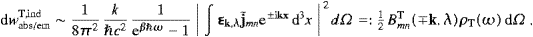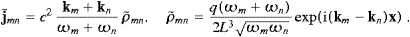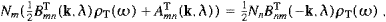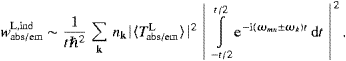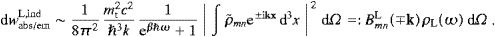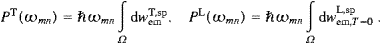Volume 320, 15 March 2003, Pages 329-356
Abstract
The emission of superluminal quanta (tachyons) by freely propagating particles is scrutinized. Estimates are derived for spontaneous superluminal radiation from electrons moving close to the speed of the Galaxy in the microwave background. This is the threshold velocity for tachyon radiation to occur, a lower bound. Quantitative estimates are also given for the opposite limit, tachyon radiation emitted by ultra-relativistic electrons in linear colliders and supernova shock waves. The superluminal energy flux is studied and the spectral energy density of the radiation is derived, classically as well as in second quantization. There is a transversal bosonic and a longitudinal fermionic component of the radiation. We calculate the power radiated, its angular dependence, the mean energy of the radiated quanta, absorption and emission rates, as well as tachyonic number counts. We explain how the symmetry of the Einstein A-coefficients connects to time-symmetric wave propagation and to the Wheeler–Feynman absorber theory. A relation between the tachyon mass and the velocity of the Local Group of galaxies is suggested.
Author Keywords: Superluminal Liénard–Wiechert potentials; Quantum tachyons; Spontaneous tachyon radiation; Detailed balancing; Longitudinal radiation; Aether
PACS classification codes: 05.30.Ch; 42.25.Bs; 11.10.Lm; 98.70.Vc
Article Outline
- 1. Introduction
- 2. Superluminal radiation fields, their energy, and the power radiated
- 3. Does a uniformly moving charge radiate?
- 4. Quantization of the superluminal spectral densities and the radiant power
- 5. Spontaneous emission and absorption outside the lightcone: Einstein coefficients for free charges
- 6. Conclusion
- Acknowledgements
- References
1. Introduction
We will explore the spontaneous emission of tachyons by uniformly moving sources. In a relativistic setting such as electrodynamics, freely moving charges do not radiate and radiating particles slow down by radiation losses. (We will consider point charges without an internal structure.) Some explanations as to the context are therefore in order.
When considering superluminal signals, we have to give up relativity or causality, as Lorentz boosts can change the time order of spacelike connections [1, 2, 3, 4 and 5]. We will maintain causality, and model superluminal signals in an absolute spacetime as defined by the expanding galaxy grid, the rest frame of the microwave background. We may try a wave theory or a particle picture as the starting point. The latter has been studied for quite some time but did not result in viable interactions of tachyons with matter [6, 7, 8 and 9]. So we suggest to model tachyons as wave fields with negative mass-square, coupled by minimal substitution to subluminal particles.
Whatever the specifics of the superluminal wave equation, there is only one Green function supported outside the light cone; it is time symmetric, half-retarded, half-advanced. To achieve fully retarded wave propagation, an absorber is needed, capable of turning advanced modes into retarded ones [10, 11, 12, 13, 14 and 15]. A causal theory of superluminal signals requires an absolute space, quite independently of the actual mechanism of signal transfer. On this basis we can identify space itself as the absorber medium, the ether, the medium of wave propagation [16].
Having settled for a wave theory, we have to define the interaction of the superluminal modes with matter. This is the crucial point; after all, what else can one expect from a theory of tachyons other than suggestions as to where to search for them? We will maintain the best established interaction mechanism, minimal substitution, by treating tachyons as a sort of photons with negative mass-square, a real Proca field minimally coupled to subluminal particles [17 and 18]. Although great care is taken to maintain the analogy to electrodynamics, there are some basic differences. There is no gauge freedom but there is longitudinal radiation, even more pronounced than the transversal counterpart, due to the mass term in the wave equation. More importantly, this is not only a theory of superluminal wave motion, but also a theory of the absolute cosmic spacetime, this cannot be disentangled. The universal frame of reference is generated by the galaxy grid; it is the rest frame of the ether, the absorber medium, as well as the rest frame of the cosmic background radiations [19 and 20]. Uniform motion and rest are distinguishable states, and in this context we will show that freely moving charges can radiate superluminal quanta. They even do so without slowing down, as the radiated energy is drained from the absorber, from the oscillators of the ether. Superluminal radiation by inertial charges is but a manifestation of the absolute nature of space.
In Section 2 we
will derive the superluminal power radiated by a classical point charge
in arbitrary motion. We will discuss transversal and longitudinal
radiation, its angular dependence, time symmetry outside the lightcone,
the absorber field, retardation, and tachyonic Liénard–Wiechert
potentials [21 and 22]. In Section 3, we
specialize to uniformly moving charges and calculate the transversal
and longitudinal spectral densities. In Section 4 these
densities are quantized, and we discuss their asymptotic limits with
respect to the speed of the radiating charge. We find a threshold
velocity, a lower bound on the speed of the source, for tachyon
radiation to occur. This is a pure quantum effect absent in the
classical theory. This threshold happens to numerically coincide with
the speed of the Galaxy in the microwave background, which suggests a
connection between the tachyon mass and the velocity of the Local Group
of galaxies in the ether,
2. Superluminal radiation fields, their energy, and the power radiated
The Proca equation [17] with
negative mass-square, Fμν,ν−mt2Aμ=c−1jμ,
can equivalently be written as (□+mt2)Aμ=−c−1jμ,
subject to the Lorentz condition A,μμ=0.
The sign conventions for tachyon mass and field tensor are mt>0
and Fμν=Aν,μ−Aμ,ν,
for metric and d'Alembertian, ημν=diag(−c2,1,1,1)
and □=ημν∂μ∂ν,
respectively. The tachyon mass mt
has the dimension of an inverse length, being a shortcut for mtc/ . We
find
. We
find ![]() , estimated from Lamb shifts in hydrogenic systems [18]. The
Lagrangian and the energy–momentum tensor of the free Proca field read
, estimated from Lamb shifts in hydrogenic systems [18]. The
Lagrangian and the energy–momentum tensor of the free Proca field read
so that FαβFαβ=−2(E2−B2). The field equations decompose into
where we identified jμ=(ρ,j). The Lorentz condition c−2∂A0/∂t=divA apparently follows from the field equations and current conservation, ∂ρ/∂t+divj=0. The vector potential is completely determined by the current and the E and B fields, there is no gauge freedom due to the tachyon mass.
We represent the spatial component of the vector potential as
,This is completely general, there are no specific assumptions on the current, other than being localized in the vicinity of the coordinate origin, a bounded domain, that is. A discussion of superluminal Green functions and the derivation of (2.4) is given in [16]. The only classical Green function outside the lightcone is time-symmetric, half-retarded, half-advanced. Its convolution with the current results in a time-symmetric vector field
The Fourier transforms of the field strengths and the time
component of the 4-potential are readily calculated by making use of ((2.2) and (2.4)) and the
Lorentz condition, ![]() . The polarized components read in leading order
. The polarized components read in leading order
To illustrate the meaning of the integral transform ![]() defined in (2.5), we
consider a subluminal particle x0(t),
defined in (2.5), we
consider a subluminal particle x0(t),
![]() ,
arbitrarily moving in the vicinity of the coordinate origin. The
particle carries a tachyonic charge q, resulting in
the current density
,
arbitrarily moving in the vicinity of the coordinate origin. The
particle carries a tachyonic charge q, resulting in
the current density
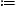 v−n(n·v)
and vL(x,t)
v−n(n·v)
and vL(x,t)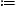 n(n·v),
and write (2.5) as
n(n·v),
and write (2.5) asThe asymptotic Liénard–Wiechert potentials and the corresponding field strengths are given by ((2.4) and (2.6)) with this
We turn to the energy density and the flux vector, which can
be read off from ((2.1) and (2.2)),
with the asymptotic fields ((2.4) and (2.6)) inserted. We have identified (ρET,ST) with T0μ, and (ρEL,SL) stands for −T0μ, so that the time-averaged densities are positive definite in either case. The averaging is readily carried out by means of the Fourier modes listed in ((2.4) and (2.6)). We find for the respective products of the transversal modes
The superscript T always stands for ‘transversal’ and is not to be confused with the time variable. In the integrand, we have already put ω=ω′ at several places, to save notation. The integral transform
will be used to avoid ill-defined squares of δ functions. According to (2.10), the time-averaged transversal flux and the energy density can be written as
where we insert the Fourier representations (2.12) to obtain
and analogously for
are substituted into
cf. (2.11), and we arrive at
The radiant power is obtained by integrating the flux through a sphere of radius r→∞,
with the solid angle element dΩ=sin θ dθ d
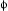 . Here, we
use the asymptotic Pointing vectors ((2.15) and (2.18)), with
the transforms
. Here, we
use the asymptotic Pointing vectors ((2.15) and (2.18)), with
the transforms In Section 4, we
will replace the classical current in the above formulas by current
matrices, appealing to the correspondence principle. To this end, we
assume the classical current to consist of a single Fourier mode ωmn:
Such truncations result in smooth limit representations of the δ function, cf. (2.13), which admit unambiguous squares. The dω and dω′ integrations in ((2.15) and (2.18)) get trivial for large T, if we use
We have defined here, cf. (2.5),
with
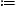 x/r.
The longitudinal current transform
x/r.
The longitudinal current transform valid up to a divergence; this is a consequence of current conservation as stated after (2.20). Hence,
Formulas ((2.22) and (2.23)) for the radiant power are exact; there is no multipole expansion involved. (We will return to them in 4 and 5, when quantizing.) The same holds for the power derived in (2.19) (with the asymptotic flux vectors ((2.15) and (2.18)) substituted), which is completely general, applying to any conserved current. In the next section we will work out the simplest example, radiation by uniformly moving charges.
3. Does a uniformly moving charge radiate?
We turn to the conceptually most interesting case,
superluminal radiation emitted by uniformly moving charges. We derive
here the classical theory, the first and second quantization will be
carried out in the subsequent sections. We consider a tachyonic charge q,
moving along the z-axis, z=vt,
0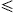 v<c,
so that ne3=cos θ,
n=x/r.
The integral transform (2.8) of the
transversal and longitudinal current projections is easily calculated:
v<c,
so that ne3=cos θ,
n=x/r.
The integral transform (2.8) of the
transversal and longitudinal current projections is easily calculated:
By making use of (2.13) and
we may write this as
The argument of the δ function in (3.3) can only get zero for cos θ>0, therefore the Heaviside function Θ(cos θ). In (3.2), the limit T→∞ can be performed without compromising the asymptotics in (2.4). In this limit, the singular accelerations inflicted by the artificial, but technically convenient discontinuous truncation in (3.1) do not show in the time averages. We thus find the transversally radiated power, cf. ((2.19) and (3.4)):
The spectral energy density is identified by a variable change according to (3.3):
with ωmax
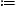 mtvγ
as the highest frequency radiated. The tachyon mass mt
is a shortcut for mtc/
mtvγ
as the highest frequency radiated. The tachyon mass mt
is a shortcut for mtc/ and γ
is the subluminal Lorentz factor (1−v2/c2)−1/2,
so that ωmax is just an mt/m
fraction of the electron energy. Another way to obtain the spectral
density is to insert ((3.2) and (3.1)) into (2.19), and to
perform the dω′ integration as above, followed by the angular
integration:
and γ
is the subluminal Lorentz factor (1−v2/c2)−1/2,
so that ωmax is just an mt/m
fraction of the electron energy. Another way to obtain the spectral
density is to insert ((3.2) and (3.1)) into (2.19), and to
perform the dω′ integration as above, followed by the angular
integration:This derivation is simpler, but conceals the angular dependence, explicit in (3.4).
The longitudinal flux is calculated via (2.18)
We thus find the longitudinal power
which in turn leads to the spectral density
with ωmax defined after (3.6). Alternatively, we may interchange the dω and the angular integrations as done in (3.7).
which coincides with (3.11). Flux vector and energy density relate in the usual way,
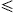 0. In
the limit θ→π/2, the emitted tachyons approach infinite speed and zero
energy. Radiation angle and frequency relate via ω=k(ω)v
cos θ. To restore the units, we have to substitute mt→mtc/
0. In
the limit θ→π/2, the emitted tachyons approach infinite speed and zero
energy. Radiation angle and frequency relate via ω=k(ω)v
cos θ. To restore the units, we have to substitute mt→mtc/ in
the above formulas. A detailed discussion of the spectral densities and
powers will be given in the next section, after quantization. The
classical formulas derived here are only valid if v/c
in
the above formulas. A detailed discussion of the spectral densities and
powers will be given in the next section, after quantization. The
classical formulas derived here are only valid if v/c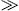 mt/m.
The Planck constant does not show in this constraint; however, the
tachyon mass already enters in the classical field equations by the
combination mtc/
mt/m.
The Planck constant does not show in this constraint; however, the
tachyon mass already enters in the classical field equations by the
combination mtc/ , cf.
the beginning of Section 2.
, cf.
the beginning of Section 2.
4. Quantization of the superluminal spectral densities and the radiant power
We will investigate how far quantization modifies the classical picture given in Section 3, tachyon radiation by a structureless particle in uniform motion. To derive the quantized version of the spectral densities ((3.6) and (3.11)), we replace the classical current by the current matrix of a subluminal quantum particle carrying tachyonic charge as outlined at the end of Section 2. In doing so, we assume the correspondence principle; in Section 5, we will demonstrate that the spectral densities and powers calculated in this way can be recovered from the spontaneous emission rates in second quantization. We will not consider spin or antiparticles, and content ourselves with positive frequency solutions of the Klein–Gordon equation. The inclusion of spin is interesting if the electron orbits in a magnetic field, resulting in tachyonic cyclotron and synchrotron radiation, but there are otherwise no conceptual changes, the current being replaced by the matrix elements of the spinor current followed by polarization averages.
We start with the Klein–Gordon equation of a subluminal
particle, c−2ψ,tt−Δψ+m2ψ=0,
where m is a shortcut for mc/ . We
define the 4-current functionals
. We
define the 4-current functionals
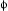 are
arbitrary solutions of the wave equation. We use the separation ansatz ψi=ui
exp(−iωit),
ωi>0, and define the
shortcuts ρmn
are
arbitrary solutions of the wave equation. We use the separation ansatz ψi=ui
exp(−iωit),
ωi>0, and define the
shortcuts ρmn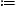 ρ(ψm,ψn)
and jmn
ρ(ψm,ψn)
and jmn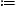 j(ψm,ψn),
as well as
j(ψm,ψn),
as well as 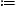 ωm−ωn.
We hence find the time-separated wave equation Δui=(m2−c−2ωi2)ui,
as well as the Hermitian current matrices
ωm−ωn.
We hence find the time-separated wave equation Δui=(m2−c−2ωi2)ui,
as well as the Hermitian current matricesWe consider periodic boundary conditions on a box of size L and conveniently normalized eigenfunctions:
with ki=2πni/L and ni
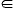 Z3. The
frequencies depend on the wave vectors via the subluminal dispersion
relation ki2=ωi2/c2−m2.
The current matrices
Z3. The
frequencies depend on the wave vectors via the subluminal dispersion
relation ki2=ωi2/c2−m2.
The current matrices 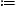 km−kn−k(ωmn)n,
n
km−kn−k(ωmn)n,
n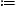 x/r.
x/r.The solid angle integration refers to the unit vector n and is easily done by means of the substitution
The total power radiated is obtained by summing over the final states and performing the continuum limit:
We introduce polar coordinates for kn, with km as polar axis, and integrate dPtotT,L over the angular variables. This is easily done by means of the δ functions in ((4.8) and (4.9)), if we replace d3kn with
where Θ is the Heaviside function. The tachyonic wave vector relates to the subluminal frequencies by
with
Emission means ωmn>0, thus we can ignore the negative root and we will write ωmax(ωm) for ωmn+. It is easy to see that ωmax is positive only if ωm>ω0, cf. (4.14), and ωmax(ω0)=0. Clearly, ωm
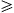 mc
from the outset. It is likewise evident that Dmn(ωmn)>0
for 0<ωmn<ωmax
and negative for larger frequencies. If ωm<ω0,
then Θ(Dmn(ωmn))
in ((4.11) and (4.12)) vanishes
for all ωmn>0, and
hence ωm>ω0
is a necessary condition for the emission of superluminal quanta. The
spectral range is 0<ωmn<ωmax,
defined by Θ(Dmn)=1.
mc
from the outset. It is likewise evident that Dmn(ωmn)>0
for 0<ωmn<ωmax
and negative for larger frequencies. If ωm<ω0,
then Θ(Dmn(ωmn))
in ((4.11) and (4.12)) vanishes
for all ωmn>0, and
hence ωm>ω0
is a necessary condition for the emission of superluminal quanta. The
spectral range is 0<ωmn<ωmax,
defined by Θ(Dmn)=1.
The total power radiated is ![]() , cf. ((4.11) and (4.12)). To
obtain the frequency distributions, we introduce ωmn
as integration variable. Using the dispersion relation for kn,
we find ωn dωmn=−c2kn
dkn and
, cf. ((4.11) and (4.12)). To
obtain the frequency distributions, we introduce ωmn
as integration variable. Using the dispersion relation for kn,
we find ωn dωmn=−c2kn
dkn and ![]() . Finally, ωmax(ωm)
. Finally, ωmax(ωm)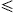 ωm−mc
for ωm>ω0,
which is easily seen from (4.15). (There is
a double zero at
ωm−mc
for ωm>ω0,
which is easily seen from (4.15). (There is
a double zero at ![]() .) Thus we can replace the upper integration boundary by ωmax
and drop Θ(Dmn)
in ((4.11) and (4.12)). We
write in the following ω for ωmn,
and define the densities pT,L(ω)
dω
.) Thus we can replace the upper integration boundary by ωmax
and drop Θ(Dmn)
in ((4.11) and (4.12)). We
write in the following ω for ωmn,
and define the densities pT,L(ω)
dω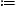 −dPtotT,L(ωmn).
We thus find, via the sub- and superluminal dispersion relations as
stated after (4.13), the
transversally and longitudinally radiated powers, the number counts,
and the respective spectral functions:
−dPtotT,L(ωmn).
We thus find, via the sub- and superluminal dispersion relations as
stated after (4.13), the
transversally and longitudinally radiated powers, the number counts,
and the respective spectral functions:
where
At the upper edge of the spectrum, we have pT(ωmax)=0,
cf. ((4.14) and (4.15)), but the
longitudinal density pL(ω)
is still positive at ωmax. It may even happen
that the integration in (4.16) is cut off
before the maximum of pL(ω)
is reached, so that pL(ω) is
increasing throughout the spectral range, cf. the discussion following (4.26). The
tachyonic mean energy is  ωavT,L
ωavT,L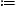 PtotT,L/NtotT,L,
the emission rates NtotT,L
(tachyons per unit time) are defined in (4.16). To get
the dimensions right in ((4.17), (4.18) and (4.19)), we
still have to rescale the masses, m(t)→m(t)c/
PtotT,L/NtotT,L,
the emission rates NtotT,L
(tachyons per unit time) are defined in (4.16). To get
the dimensions right in ((4.17), (4.18) and (4.19)), we
still have to rescale the masses, m(t)→m(t)c/ . The
integrals in (4.16) are
elementary, and we find the total transversally emitted power and the
transversal count rate as
. The
integrals in (4.16) are
elementary, and we find the total transversally emitted power and the
transversal count rate as
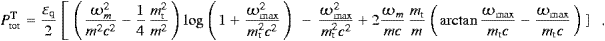
Here, ωmax is the break frequency defined in (4.17), the power scale is set by
and 0<arctan<π/2. The longitudinal power and count rate are
with ω0 defined in (4.17).
For the rest of this section, we will study asymptotic limits
of the spectral densities, powers and number counts derived above.
There are three asymptotic regimes giving a comprehensive picture of
the radiation. To see this, we introduce the shortcut ![]() and write ωm=mcγ,
with the subluminal γ=(1−v2/c2)−1/2.
Since ωm>ω0,
we have apparently α<1 or
and write ωm=mcγ,
with the subluminal γ=(1−v2/c2)−1/2.
Since ωm>ω0,
we have apparently α<1 or
It is evident that ωmax<ωmmt/m. If α2
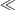 mt2/m2
mt2/m2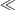 1,
which defines the extreme non-relativistic regime, we find ωmax≈mcα2.
In the non-relativistic limit, mt2/m2
1,
which defines the extreme non-relativistic regime, we find ωmax≈mcα2.
In the non-relativistic limit, mt2/m2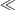 α2
α2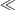 1,
we find ωmax≈mtcα.
In the ultra-relativistic regime, with α2≈1 (and
mt2/m2
1,
we find ωmax≈mtcα.
In the ultra-relativistic regime, with α2≈1 (and
mt2/m2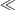 1),
we find ωmax≈mtc(1−α2)−1/2.
This is to be compared to ωm≈mc
in the two non-relativistic regimes, and to ωm≈mc(1−α2)−1/2
in the ultra-relativistic limit. (All these estimates are meant as
leading orders in asymptotic double series expansions.) The extreme
non-relativistic limit only applies to a very narrow velocity range, to
velocities close to the threshold vmin,
which is evident from γ=(1−α2)−1/2γmin.
1),
we find ωmax≈mtc(1−α2)−1/2.
This is to be compared to ωm≈mc
in the two non-relativistic regimes, and to ωm≈mc(1−α2)−1/2
in the ultra-relativistic limit. (All these estimates are meant as
leading orders in asymptotic double series expansions.) The extreme
non-relativistic limit only applies to a very narrow velocity range, to
velocities close to the threshold vmin,
which is evident from γ=(1−α2)−1/2γmin.
We can now compare the foregoing to the classical radiation
theory of Section 3. The
upper edge of the spectrum, ωmax in (4.24), coincides
with its classical counterpart defined after (3.6) in the
limit mt2/m2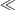 α2.
This is the condition for the classical theory to apply. In this limit
we can apparently identify α≈v/c,
and it is also evident that ωm
α2.
This is the condition for the classical theory to apply. In this limit
we can apparently identify α≈v/c,
and it is also evident that ωm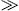 ωmax (where ωmax
is the highest frequency radiated, and ωm
is the energy of the source). In the transversal spectral density (4.18), we may
therefore replace ω0 by mc
and drop the subsequent term ωmω,
in this way recovering the classical density (3.6). The same
reasoning applies to the longitudinal density pL(ω),
which coincides with the classical formula (3.11) if we drop
the ωmω and ω2/4
terms in (4.19). The
powers ((4.20) and (4.22)) are
turned into the classical ones in ((3.5) and (3.10)), by
discarding all terms explicitly depending on the mt/m
ratio.
ωmax (where ωmax
is the highest frequency radiated, and ωm
is the energy of the source). In the transversal spectral density (4.18), we may
therefore replace ω0 by mc
and drop the subsequent term ωmω,
in this way recovering the classical density (3.6). The same
reasoning applies to the longitudinal density pL(ω),
which coincides with the classical formula (3.11) if we drop
the ωmω and ω2/4
terms in (4.19). The
powers ((4.20) and (4.22)) are
turned into the classical ones in ((3.5) and (3.10)), by
discarding all terms explicitly depending on the mt/m
ratio.
The peak frequency of the transversal spectral density pT(ω),
cf. (4.18), is a zero
of
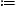 ωpeakT/ωm.
We calculate this maximum in the three asymptotic regimes enumerated
above. If α2
ωpeakT/ωm.
We calculate this maximum in the three asymptotic regimes enumerated
above. If α2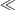 mt2/m2
mt2/m2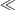 1,
we can ignore the fourth order in (4.25) as well as
the second, and find ωpeakT≈mcα2/2,
just in the middle of the spectral range. If mt2/m2
1,
we can ignore the fourth order in (4.25) as well as
the second, and find ωpeakT≈mcα2/2,
just in the middle of the spectral range. If mt2/m2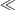 α2
α2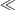 1,
we find, by dropping the fourth and first-order terms,
1,
we find, by dropping the fourth and first-order terms, The maximum of the longitudinal spectral function (4.19) is found
by solving
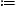 ωpeakL/ωm,
and we may always assume mtc/ωm
ωpeakL/ωm,
and we may always assume mtc/ωm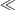 1.
There are two positive solutions; the first, yL≈2,
lies outside the integration range in (4.16), the
relevant one is ωpeakL≈mtc,
stemming from the second and zeroth orders of (4.26). Also this
peak lies beyond ωmax if α2
1.
There are two positive solutions; the first, yL≈2,
lies outside the integration range in (4.16), the
relevant one is ωpeakL≈mtc,
stemming from the second and zeroth orders of (4.26). Also this
peak lies beyond ωmax if α2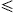 1/2,
since ωmax≈mtc
for α2≈1/2. Hence, if α2
1/2,
since ωmax≈mtc
for α2≈1/2. Hence, if α2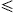 1/2,
then pL(ω) is increasing
throughout the spectral range; if α2
1/2,
then pL(ω) is increasing
throughout the spectral range; if α2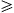 1/2, it
admits a maximum at ωpeakL≈mtc
like the transversal density.
1/2, it
admits a maximum at ωpeakL≈mtc
like the transversal density.
We turn to the asymptotic limits of the radiant powers and the
count rates in ((4.20) and (4.22)). In the
extreme non-relativistic regime, α2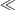 mt2/m2
mt2/m2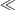 1,
1,
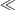 α2
α2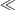 1,
1,The non-relativistic mean frequencies ωavT,L are close to the transversal spectral peak ωpeakT. In the extreme relativistic regime, α2≈1, we find
and the same formulas for the longitudinal radiation with the −1 after the log-terms dropped. The parameter α defining the three asymptotic regimes has been introduced after (4.22); it relates to the subluminal velocity of the source and the tachyon mass by
We still have to rescale the masses, m(t)→m(t)c/
 , in
all formulas of this section, and we define the tachyonic fine
structure constant as αq
, in
all formulas of this section, and we define the tachyonic fine
structure constant as αq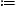 q2/(4π
q2/(4π c),
which is not to be confused with the expansion parameter α. We
illustrate the quantities listed in ((4.27), (4.28) and (4.29)) with a
freely moving electron as source. The electron–tachyon mass ratio is mt/m≈1/238,
resulting in a tachyonic Compton wavelength of
c),
which is not to be confused with the expansion parameter α. We
illustrate the quantities listed in ((4.27), (4.28) and (4.29)) with a
freely moving electron as source. The electron–tachyon mass ratio is mt/m≈1/238,
resulting in a tachyonic Compton wavelength of  /(mtc)≈0.92
Å, and the quotient of tachyonic and electric fine structure constants
reads αq/αe≈1.4×10−11,
inferred from Lamb shifts in hydrogenic systems [18]. We will use
αq≈1.0×10−13 and mt≈2.15
keV/c2. The quantities in ((4.27), (4.28) and (4.29)) can
easily be assembled with these ratios and mtc2/
/(mtc)≈0.92
Å, and the quotient of tachyonic and electric fine structure constants
reads αq/αe≈1.4×10−11,
inferred from Lamb shifts in hydrogenic systems [18]. We will use
αq≈1.0×10−13 and mt≈2.15
keV/c2. The quantities in ((4.27), (4.28) and (4.29)) can
easily be assembled with these ratios and mtc2/ ≈3.27×1018
s−1.
≈3.27×1018
s−1.
As an example for the extreme non-relativistic limit (4.27), we assume the electron at vLG/c≈2.10×10−3, which is the velocity of the Galaxy in the microwave background, inferred from the dipole anisotropy of the background temperature, cf. the review article of Smoot and Scott in [23]. This speed coincides with the threshold velocity vmin in (4.23), recovered by putting α=0 in (4.30). This suggests that the velocity of the Local Group in the ether is linked to the tachyon mass as stated in (1.1). I do not have a real explanation for that, perhaps it is just a coincidence, but it is most intriguing indeed that vLG is the speed at which free electrons cease to emit tachyons, cease to drain energy from the ether.
In the extreme non-relativistic regime, α2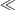 mt2/m2
(that is 0<α
mt2/m2
(that is 0<α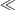 10−3),
the electronic speed (parametrized as in (4.30)) is
virtually independent of α, and very nearly coincides with the
threshold velocity. We find with the above constants, cf. (4.27):
10−3),
the electronic speed (parametrized as in (4.30)) is
virtually independent of α, and very nearly coincides with the
threshold velocity. We find with the above constants, cf. (4.27):
 ωpeakT,L=mtc2(vtach2/c2−1)−1/2.
For α→0, the peak frequencies converge to zero, so that vtach/c≈mtc2/(
ωpeakT,L=mtc2(vtach2/c2−1)−1/2.
For α→0, the peak frequencies converge to zero, so that vtach/c≈mtc2/( ωpeakT,L)
can attain virtually any value, with modest energy transfer, however.
This applies to electrons freely propagating very close to the speed of
the Local Group, vLG≈627
km/s, below this threshold no tachyons can be emitted in uniform
motion.
ωpeakT,L)
can attain virtually any value, with modest energy transfer, however.
This applies to electrons freely propagating very close to the speed of
the Local Group, vLG≈627
km/s, below this threshold no tachyons can be emitted in uniform
motion.
The normal non-relativistic regime as defined by (4.28) is covered
by 10−3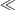 α
α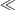 1;
in this case we may identify α≈v/c,
cf. (4.30), and find
1;
in this case we may identify α≈v/c,
cf. (4.30), and find
Next-generation linear colliders will yield electrons with E≈0.5
TeV or γ≈9.785105 and our first
ultra-relativistic example. In (4.29) we put 1−α2≈γ−2,
and find
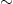 γ. For instance, electrons shock-accelerated to E≈200
TeV (γ≈3.91×108) in supernova remnants [25, 26 and 27] radiate
γ. For instance, electrons shock-accelerated to E≈200
TeV (γ≈3.91×108) in supernova remnants [25, 26 and 27] radiate ωpeakT,L
as in (4.33). At this
point, one could be tempted to define a radiation lifetime, something
like E/P. However, tachyon
radiation is generated by a time-symmetric Green function and an
absorber field. Contrary to electromagnetic radiation, there is no
deceleration due to radiation loss, the energy spontaneously radiated
is contained in the absorber field, supplied by the oscillators of the
absorber. In the next section, we will demonstrate that the classical
time symmetry (discussed after (2.5)) has its
quantal counterpart in the symmetry of the Einstein A-coefficients,
the spontaneous emission being balanced by spontaneous absorption.
ωpeakT,L
as in (4.33). At this
point, one could be tempted to define a radiation lifetime, something
like E/P. However, tachyon
radiation is generated by a time-symmetric Green function and an
absorber field. Contrary to electromagnetic radiation, there is no
deceleration due to radiation loss, the energy spontaneously radiated
is contained in the absorber field, supplied by the oscillators of the
absorber. In the next section, we will demonstrate that the classical
time symmetry (discussed after (2.5)) has its
quantal counterpart in the symmetry of the Einstein A-coefficients,
the spontaneous emission being balanced by spontaneous absorption.
5. Spontaneous emission and absorption outside the lightcone: Einstein coefficients for free charges
We will study induced and spontaneous radiation in second
quantization. A non-relativistic example to that effect, tachyonic
transitions between bound states in a Coulomb potential, has already
been given in [24]. Here, we
consider tachyon radiation by freely propagating electrons. In this
case, the Einstein coefficients can be calculated without multipole
approximations. The B-coefficients reflect the
symmetry of the induced radiation, however, the A-coefficients
are symmetric as well. In electrodynamics, there is no time-symmetric
counterpart to spontaneous emission, but outside the lightcone there is
spontaneous absorption, the radiated energy being recovered from the
absorber medium. The Green function is time symmetric, and so is
spontaneous radiation. The spontaneous absorption corresponds to the
advanced component of the classical radiation field, cf. Section 2. The
quantum statistics of the free tachyon field was studied in [20], we repeat
some formulas needed to compile the matrix elements of the Hamiltonian.
Then we calculate and balance the emission rates for uniformly moving
charges. Finally we show that the spectral densities ((4.18) and (4.19)) derived
by means of the correspondence principle survive the second
quantization. In this paper, the Fourier transforms of the dielectric
and magnetic permeabilities of the ether are put equal to one, ![]() , that is, we assume a negligible refractivity and absorptivity, cf. [20]. Otherwise
we would have to specify more parameters, apart from the tachyon mass
and the tachyonic fine structure constant.
, that is, we assume a negligible refractivity and absorptivity, cf. [20]. Otherwise
we would have to specify more parameters, apart from the tachyon mass
and the tachyonic fine structure constant.
We start with the plane wave decomposition of the spatial
component of the vector potential
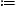 2πn/L.
The summation is over integer lattice points n
in R3, corresponding to
periodic boundary conditions in (2.3), so that
the L−3/2exp(ikx)
are orthonormal and complete in a box of size L.
The
2πn/L.
The summation is over integer lattice points n
in R3, corresponding to
periodic boundary conditions in (2.3), so that
the L−3/2exp(ikx)
are orthonormal and complete in a box of size L.
The  k,1
and
k,1
and  k,2
are arbitrary real unit vectors (linear polarization vectors)
orthogonal to
k,2
are arbitrary real unit vectors (linear polarization vectors)
orthogonal to  k,3
k,3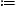 k0=k/|k|,
so that the
k0=k/|k|,
so that the  k,λ
constitute an orthonormal triad for every n.
The amplitudes â(k,λ) are arbitrary
complex numbers.
k,λ
constitute an orthonormal triad for every n.
The amplitudes â(k,λ) are arbitrary
complex numbers.
The Fourier coefficients Â0(k)
of the time component A0(x,t)
of the 4-potential are defined as in (5.1), and the
same holds for the field strengths,
has to be satisfied, which we henceforth assume; ω and k
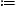 |k|
are positive.
|k|
are positive.
We split the potential and the field strengths into
transversal and longitudinal components:
The interference term of the longitudinal and transversal modes vanishes in the averaging procedure. The sign change of the longitudinal components of energy and flux, anticipated in (2.11), will be effected by Fermi statistics. By comparing the individual modes in these series, we find
The group velocity vgr follows from the dispersion relation (5.3), dω/dk=c2k/ω, cf. the discussion after (3.12). We introduce rescaled Fourier coefficients ak,λ in the preceding time averages,
where λ=1,2, so that the field energy and the flux get amendable to statistical interpretation
These time averages are the starting point for quantization. We sketch here only very shortly the overall reasoning, for details see [20]. The Fourier coefficients ak,λ are interpreted as operators, and the complex conjugates ak,λ* as their adjoints ak,λ+. We use commutation relations, [ak,λ, ak′,λ′+]=δkk′δλλ′, for the transversal modes λ=1,2, which admit the occupation number representation
Anticommutators, [ak,3,ak′,3+]+=δkk′, are employed for the longitudinal modes, to turn the longitudinal energy (5.9) into a positive definite operator. These Fermi operators admit the representation
where the occupation numbers are now restricted to zero and one. The time-averaged transversal Hamilton operator for the free tachyon field and the transversal flux operator are thus given in (5.8), with the Fourier amplitudes ak,λak,λ* replaced by the operator product ak,λ+ak,λ. The energy and flux operators of the longitudinal radiation are obtained by the substitution ak,3ak,3*→−ak,3+ak,3 in (5.9). The partition function is easily assembled, the lattice sums being replaced by the continuum limit [28 and 29], and we find the spectral densities of the transversal and longitudinal radiations as
We turn to the interaction with subluminal matter. As in Section 4, we
consider a spinless quantum particle, a Klein–Gordon field coupled to
the tachyonic vector potential by minimal substitution. We write the
Lagrangian of the coupled system as L=LP+Lψ,
with the Lagrangian LP of
the free Proca field as in (2.1), and
the second equality is valid up to a divergence, and we used the free field equation as stated before (4.1). The 4-current, the time separation, and the spectral resolution are given in ((4.1), (4.2) and (4.3)). We expand the free Klein–Gordon field,
 ωnbnbn*,
via the orthonormality (4.3). In the
4-current (4.1), we at
first put
ωnbnbn*,
via the orthonormality (4.3). In the
4-current (4.1), we at
first put 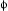 =ψ and then
expand the wave field, so that
=ψ and then
expand the wave field, so thatwith
up to terms of O(q2). Hence, by means of (4.1),
Here we substitute the Fourier expansions (5.15) as well as those of the tachyon field defined by ((5.1), (5.4) and (5.7)). Finally, we replace the bmbn* in (5.15) by operator products bn+bm, and the tachyonic field amplitudes ak,λ(*) by operators ak,λ(+) as done after (5.11) for the free field. The subluminal spinless Klein–Gordon field is quantized in Bose statistics, [bm,bn+]=δmn, so that the representation (5.10) is applicable, and the (anti)commutator brackets and representations for the tachyonic operators ak,λ(+) are stated in ((5.10) and (5.11)).
First we study interaction with transversal tachyons. We
consider a fixed linear polarization λ (that is, no summation over λ in
the Fourier series). The transversal component of the interaction
Hamiltonian (5.17) reads HintT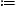 −
− −1c−3ATj(ψ),
where we substitute the Fourier decompositions ((5.1), (5.4) and (5.7)), and (5.15),
−1c−3ATj(ψ),
where we substitute the Fourier decompositions ((5.1), (5.4) and (5.7)), and (5.15),
The nk are tachyonic occupation numbers for a state of polarization λ. At this point, k is a discrete lattice vector, cf. (5.1). The
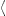 Tabs,emT
Tabs,emT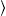 just
differ by a sign change of the wave vector in the exponential. (The
upper sign always refers to absorption.) The preceding formulas are
standard time-dependent perturbation theory with a periodic potential [30]; the nk-dependent
factors stem from the bosonic representation (5.10). The
tachyonic wave vector k relates to the
tachyonic frequency ωk by the
dispersion relation (5.3); k
and ωk are positive, and the ωmn
just
differ by a sign change of the wave vector in the exponential. (The
upper sign always refers to absorption.) The preceding formulas are
standard time-dependent perturbation theory with a periodic potential [30]; the nk-dependent
factors stem from the bosonic representation (5.10). The
tachyonic wave vector k relates to the
tachyonic frequency ωk by the
dispersion relation (5.3); k
and ωk are positive, and the ωmn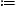 ωm−ωn
refer to energy levels of the free wave equation, cf. (4.3). The
initial state will be denoted by a subscript m and
the final state by n, so that a positive ωmn
stands for emission.
ωm−ωn
refer to energy levels of the free wave equation, cf. (4.3). The
initial state will be denoted by a subscript m and
the final state by n, so that a positive ωmn
stands for emission.
We turn to the longitudinal component of the interaction (5.17), HintL=HintL(1)+HintL(2),
where HintL(1)=− −1c−3ALj(ψ)
and HintL(2)=−
−1c−3ALj(ψ)
and HintL(2)=− −1c−3A0ρ(ψ),
with the Fourier series for AL
and A0 defined in ((5.1) and (5.4)) and (5.7). We find,
analogously to (5.18),
−1c−3A0ρ(ψ),
with the Fourier series for AL
and A0 defined in ((5.1) and (5.4)) and (5.7). We find,
analogously to (5.18),
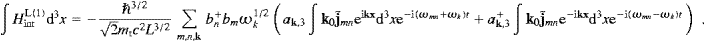
We have here restored the units, mt→mtc/
 . The
longitudinal operators ak,3(+)
anticommute, the representation (5.11) applies,
and we assemble the matrix elements of the longitudinal interaction
operator as
. The
longitudinal operators ak,3(+)
anticommute, the representation (5.11) applies,
and we assemble the matrix elements of the longitudinal interaction
operator asHere, nk is an occupation number in Fermi statistics, zero or one, and (−)n<m denotes the sign factor occurring in the fermionic representation (5.11); k0=k/k is the tachyonic unit wave vector. The generalization of the matrix elements ((5.19) and (5.21)) to a refractive and absorptive spacetime can be found in [20]. Finally we return to ((4.1), (4.2) and (4.3)), and inspect the integral ∫(umΔun*−un*Δum)e±ikx d3x, once by applying the Gauss theorem, and once by using the Klein–Gordon equation. In this way we derive
where we used energy conservation, ωk=
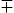 ωmn in (5.21), as well
as the tachyonic dispersion relation (5.3) (with mt→mtc/
ωmn in (5.21), as well
as the tachyonic dispersion relation (5.3) (with mt→mtc/ .)
.)
Once the matrix elements are known, the transition rate for
transversally induced absorption and emission in a given polarization λ
is obtained by a standard procedure [30],
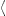 nk
nk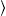 =(eβ
=(eβ ωk−1)−1,
cf. (5.12). dΩ=sin θ
dθ d
ωk−1)−1,
cf. (5.12). dΩ=sin θ
dθ d , the solid
angle element of the tachyonic wave vector, and k(ω)
is given in (5.3). The same
formula also applies to spontaneous radiation, wemT,sp,
but with the
, the solid
angle element of the tachyonic wave vector, and k(ω)
is given in (5.3). The same
formula also applies to spontaneous radiation, wemT,sp,
but with the  nk
nk -factor
dropped, since wemT,sp
stems from the +1 under the root in (5.19). In the
limit t→∞, the dω-integration in (5.23) gets
trivial, and by substituting (5.19) we find
-factor
dropped, since wemT,sp
stems from the +1 under the root in (5.19). In the
limit t→∞, the dω-integration in (5.23) gets
trivial, and by substituting (5.19) we findwhere ω (and k(ω)) is taken at |ωmn|. The upper sign refers to absorption, and m to the initial state. The transversal tachyonic spectral density ρT is defined in (5.12). (The spectral densities in (5.12) refer to the tachyonic heat bath triggering the induced radiation.) The total emission rate is dwemT=dwemT,ind+dwemT,sp. In equilibrium, induced emission and absorption compensate each other, due to the detailed balancing symmetry BmnT(k,λ)=BnmT(−k,λ), which follows from the hermiticity of the current matrices (4.2). The spontaneous emission of transversal tachyons is temperature independent, unaffected by the tachyonic heat bath, in contrast to the longitudinal emission discussed below. The unpolarized transversal radiation rates are obtained by replacing
 k/k
and
k/k
andcf. ((4.2) and (4.3)).
The spontaneous emission rate (5.25) is
symmetric, AmnT(k,λ)=AnmT(−k,λ),
reflecting the time symmetry of the classical radiation field, cf. Section 2. (The
radiation discussed in the previous sections is all spontaneous.) The
retarded field, which we have quantized, results from the absorber
field complementing the time-symmetric field of the particle, as
pointed out after (2.5). The net
energy balance of the time-symmetric field is zero, as the spontaneous
emission of a tachyon is accompanied by the absorption of an absorber
quantum. This restores the initial state of the source in the reverse
transition. Spontaneous absorption stands as the quantal analog to the
advanced modes of the time-symmetric classical wave field. Induced
transitions are not affected by the absorber field, and in equilibrium
induced emission and absorption cancel each other, due to the mentioned
symmetry of the B-coefficients. In the energy
balance for the equilibrium distribution ρT(ω)
in (5.12), the
different Boltzmann weights are accounted for by the A-coefficients,
 ωmn),
quite independent of the statistics.
ωmn),
quite independent of the statistics.
We turn to longitudinal radiation. The induced
absorption/emission rate for longitudinal tachyons is composed
analogously to the transversal rates (5.23),
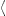 Tabs/emL
Tabs/emL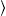 in (5.22). The
fermionic occupation numbers are replaced in the continuum limit by the
averages
in (5.22). The
fermionic occupation numbers are replaced in the continuum limit by the
averages 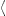 nk
nk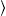 =(eβ
=(eβ ωk+1)−1,
cf. (5.12). Hence,
ωk+1)−1,
cf. (5.12). Hence,where m denotes the initial state, both for absorption and emission, and ω=|ωmn|. The longitudinal spontaneous emission is identified as follows. The nk in (5.21) can only take the values zero and one, so that the factor 1−nk does not change if squared. Thus the total emission rate is dwemL=dwem,T=0L,sp−dwemL,ind, with dwemL,ind as defined by (5.29) and
This is the spontaneous transition rate in the zero temperature limit, obtained from (5.28) with the nk-factors dropped. At finite temperature, the spontaneous emission is dwemL,sp=dwem,T=0L,sp−2dwemL,ind, so that the total emission dwemL=dwemL,ind+dwemL,sp. Hence,
which reduces in the absence of a tachyonic heat bath to dwem,T=0L,sp The basic symmetries BmnL(k)=BnmL(−k) and AmnL(k)=AnmL(−k) also extend to longitudinal radiation, so that the induced transitions cancel each other, and a spontaneous transition is instantaneously restored by an absorber quantum. The longitudinal spontaneous emission (5.31) is temperature dependent and vanishes in the high temperature limit. At finite temperature, the equilibrium condition, cf. (5.27),
requires the longitudinal density ρL(ω) in (5.12).
I take this opportunity to correct a mistake in the dipole
approximation of the longitudinal transition probability calculated in [20]. The squared
ratio  ωji/(mtc2)
in (5.17), (5.23) and (5.27) of [20] should be
inverted. At 2.2 MeV, the ratio of the longitudinal and transversal
dipole transition rates reads ωL/ωT≈3.8×10−7,
from which we conclude that the longitudinal background radiation has
reached equilibrium within 1018 s. This is to be
compared with a cosmic age of H0−1≈14
Gyr≈4.4×1020 s. The reasoning behind this is
explained in [20].
ωji/(mtc2)
in (5.17), (5.23) and (5.27) of [20] should be
inverted. At 2.2 MeV, the ratio of the longitudinal and transversal
dipole transition rates reads ωL/ωT≈3.8×10−7,
from which we conclude that the longitudinal background radiation has
reached equilibrium within 1018 s. This is to be
compared with a cosmic age of H0−1≈14
Gyr≈4.4×1020 s. The reasoning behind this is
explained in [20].
At zero temperature, the power spontaneously radiated by a
freely propagating charge was calculated in Section 4 by
means of the correspondence principle, which amounts to identify in ((2.20), (2.21), (2.22), (2.23), (2.24), (2.25) and (2.26)) ![]() and
and ![]() with the
hermitian current matrices
with the
hermitian current matrices ![]() and
and ![]() in (5.26). The
powers ((4.20) and (4.22)) can be
recovered from the emission rates dwemT,sp
and dwem,T=0L,sp
in ((5.24), (5.25) and (5.29)), and (5.30). The
angular-integrated power radiated at ω=ωmn
is apparently
in (5.26). The
powers ((4.20) and (4.22)) can be
recovered from the emission rates dwemT,sp
and dwem,T=0L,sp
in ((5.24), (5.25) and (5.29)), and (5.30). The
angular-integrated power radiated at ω=ωmn
is apparently
6. Conclusion
The absorber theory [12] was motivated by Dirac's covariant version of radiation damping [15], where the absorber field, half-retarded minus half-advanced, enters as Lorentz force. In the non-relativistic derivation of Abraham and Lorentz [14] it does so as well, of course, but in a less explicit way. In any case, this field is not perceived as stemming from an absorber medium, but rather as generated by the charge itself. In Dirac's theory, the absorber field does not show as radiation field in the equations of motion, but is exclusively applied along the trajectory of the charge, defining the damping force. Here we have elaborated on superluminal radiation fields at large distance from the source, the opposite limit. The asymptotic fields are quite sufficient to calculate the spectral densities and the radiant power, classically as well as in second quantization. It is not advisable to rely on the short distance behavior of Green functions; the self-energy problem indicates that the Maxwell theory may just be the asymptotic limit of a non-linear Born–Infeld type of electrodynamics [31]. If so, one cannot use the linearized theory in the vicinity of the radiating sources. The same holds for the Proca field.
Wheeler and Feynman designed the absorber theory for electrodynamics, and they interpreted the half-retarded minus half-advanced Liénard–Wiechert potential, cf. Section 2, as generated by an absorber medium, which they proposed to be the collection of electric charges in the universe [12]. They used this potential in an action-at-a-distance electrodynamics [10, 11 and 13], in an attempt to solve the radiation damping problem. In the Maxwell theory, we do not consider an absorber medium because there is a retarded Green function. Outside the lightcone, however, retardation can only be achieved by an absorber field, as the Green function supported there is time symmetric. A causal theory of superluminal signals needs an absolute spacetime, since Lorentz boosts do not preserve the time order in spacelike connections. Once the absolute nature of space is acknowledged, it is only a small step to identify space itself as the absorber medium, the ether, whose microscopic oscillators generate the absorber field [16 and 20].
I conclude by comparing the absolute spacetime underlying superluminal radiation to the relativistic spacetime view. Radiation by inertial charges may be unimaginable in relativity theory, but in the absolute cosmic spacetime this is easy to comprehend, since accelerated and inertial frames are treated on the same basis. There is a universal reference frame, the rest frame of the ether, generated by the comoving galaxy grid and manifested by the microwave background and other background radiations. The spectral density of the radiation is determined by the velocity of the uniformly moving charge. This is not a relative velocity, it stands for the absolute motion of the charge in the ether. Relative velocities only affect the appearance of the radiation in moving frames. In the rest frames of inertial observers, the radiation field may appear advanced, the transversal and longitudinal modes may appear tangled, or they may not appear at all, as it happens in the rest frame of the radiating charge [24], but all this is a consequence of the observer's individual motion. Whatever the appearance of the superluminal radiation field in a moving frame, the observer can infer the radiation in the rest frame of the ether (such as the power, the spectral densities and the frequencies radiated) by measuring the absolute velocity of the charge in the microwave background.
More generally, the relativity principle asserts that the laws of nature are the same in all inertial frames, in particular, uniform motion and rest are not distinguishable in this respect. In the absolute cosmic spacetime, the laws of nature are inherent in the rest frame of the ether, and their appearance in inertial frames is determined by the observer's state of motion. This is in sharp contrast to relativity theory, where the laws of nature are thought of as attached to individual and equivalent inertial frames. The absolute spacetime concept is centered at the state of rest, tantamount to the universal reference frame generated by the galaxy grid. Particles move in the ether, subjected to the flow of cosmic time as defined by the galactic recession, without resort to the inertial frames and proper times of individual observers. This is again in strong contrast to relativity theory, where inertial frames are the substitute for the universal rest frame. In the absolute cosmic spacetime, the crucial distinction is not between inertial and accelerated frames, but simply between motion and rest, and therefore it is not surprising that uniformly moving charges radiate.
Acknowledgements
The author acknowledges the support of the Japan Society for the Promotion of Science. The hospitality and stimulating atmosphere of the Centre for Nonlinear Dynamics, Bharathidasan University, Trichy, the Institute of Mathematical Sciences, Madras, and the Tata Institute of Fundamental Research, Bombay, are likewise gratefully acknowledged. I would like to thank Nandor Balazs and George Contopoulos for exciting discussions.



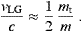
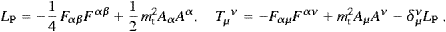
 A0−∂A/t),
Fij=
A0−∂A/t),
Fij=