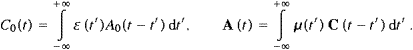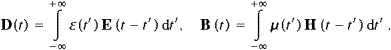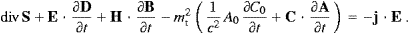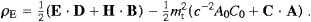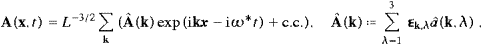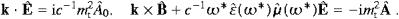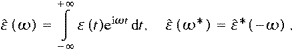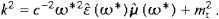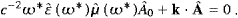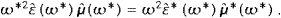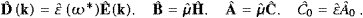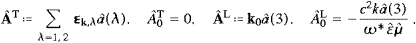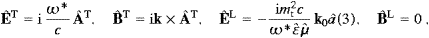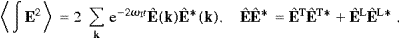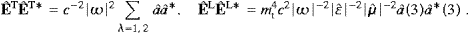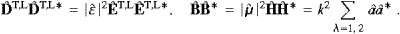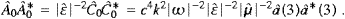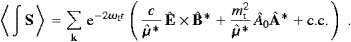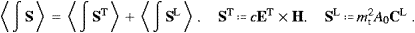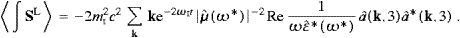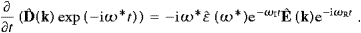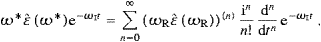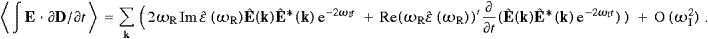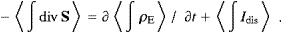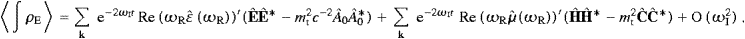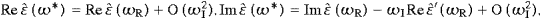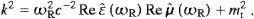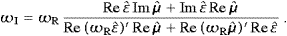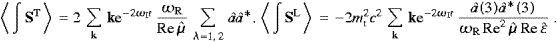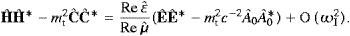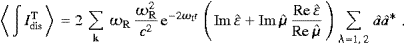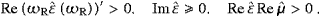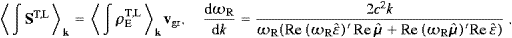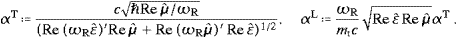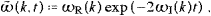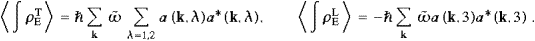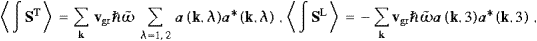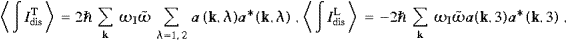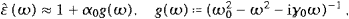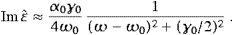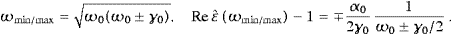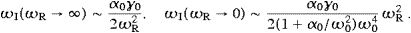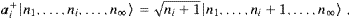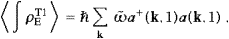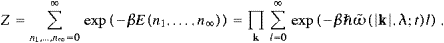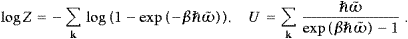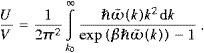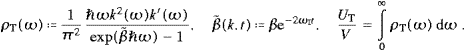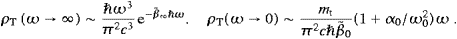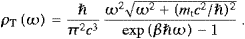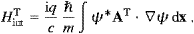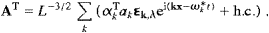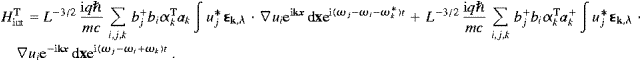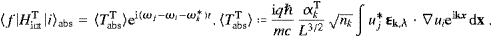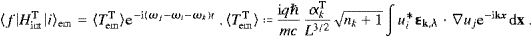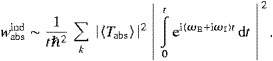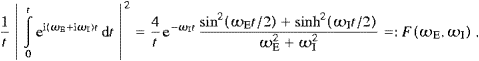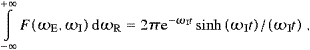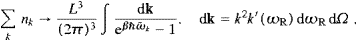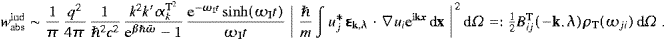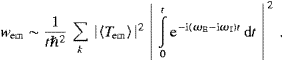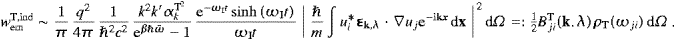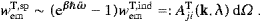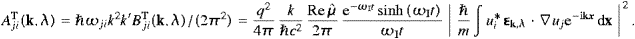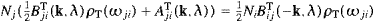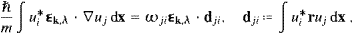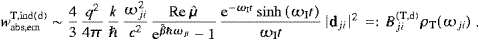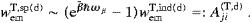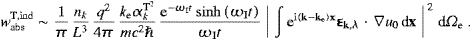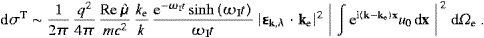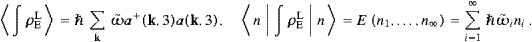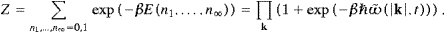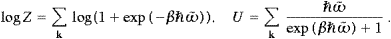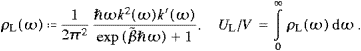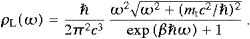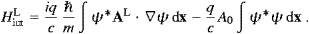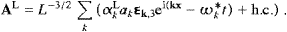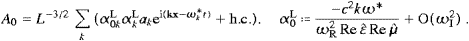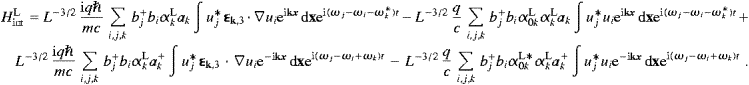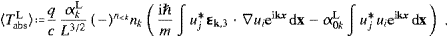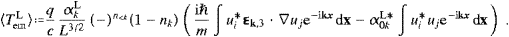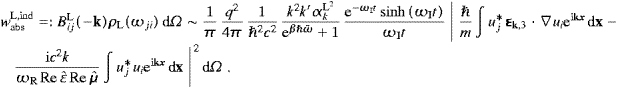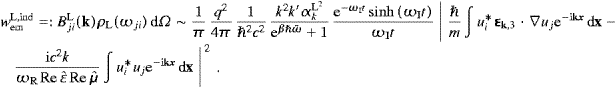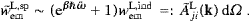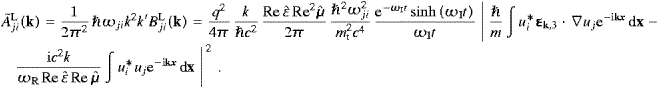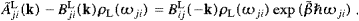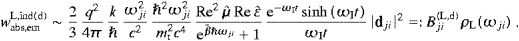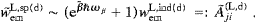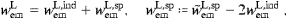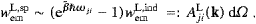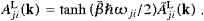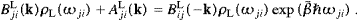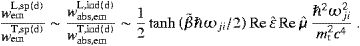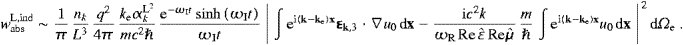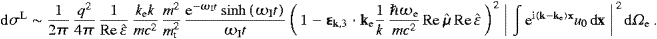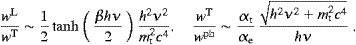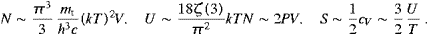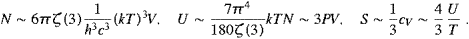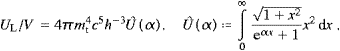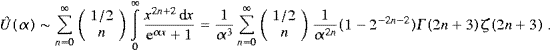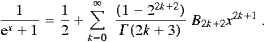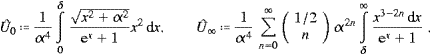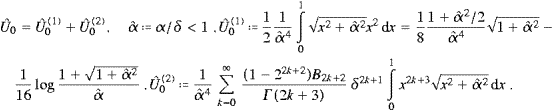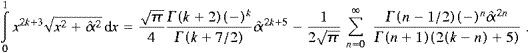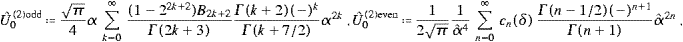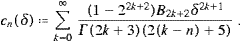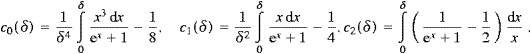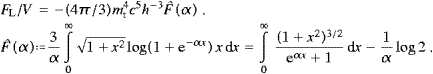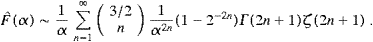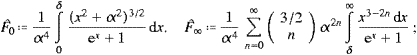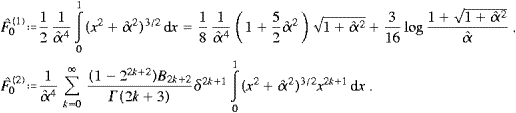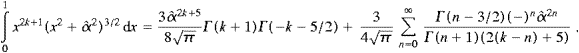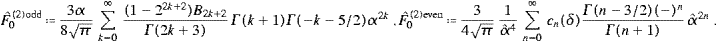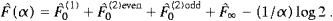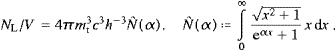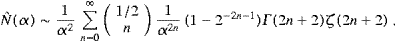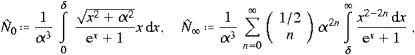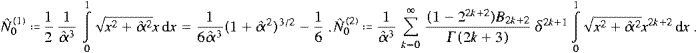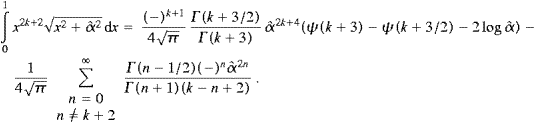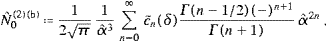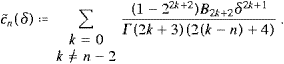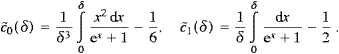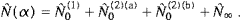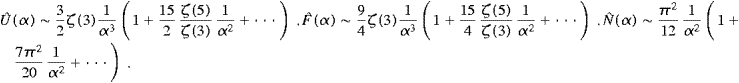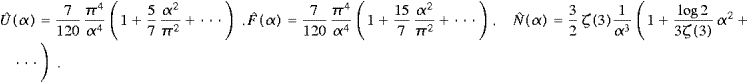Volume 307, Issues 3-4, 1 May 2002, Pages 375-404
Abstract
A statistical quantization of superluminal (tachyon) radiation is introduced. The tiny tachyonic fine structure constant suggests to depart from the usual quantum field theoretic expansions, and to use more elementary methods such as detailed equilibrium balancing of emission and absorption rates. Instead of commencing with an operator interpretation of the wave function, we quantize the time-averaged energy functional and the energy-balance equation. This allows to use different statistics for different types of modes. Transversal superluminal modes are quantized in Bose statistics, longitudinal ones are turned into fermions, resulting in a positive definite Hamiltonian for the radiation field. We discuss the absorptive space structure underlying superluminal quanta and the energy dissipation related to it. This dissipation leads to an adiabatic time variation of the temperature in the bosonic and fermionic spectral functions, gray-body quasi-equilibrium distributions with a dispersion relation adapted to the negative mass-square of the tachyonic modes. The superluminal radiation field couples by minimal substitution to subluminal matter. Adiabatically damped Einstein coefficients are obtained by detailed balancing, as well as emission and absorption rates for tachyon radiation in hydrogenic systems, in particular the possibility of spontaneous emission of superluminal fermionic quanta is pointed out, and time scales for the approach to equilibrium are derived.
Author Keywords: Tachyonic gray-body radiation; Longitudinal background radiation; Superluminal quantum ensembles; Ether; Superluminal energy dissipation; Quantum tachyons; Spontaneous tachyon emission
PACS classification codes: 05.30.Ch; 42.25.Bs; 32.70.Cs; 98.70.Vc
Article Outline
- 1. Introduction
- 2. Tachyons in a permeable spacetime
- 3. Energy balance for superluminal radiation in a refractive and absorptive space–time
- 4. Transversal tachyons in Bose-Einstein statistics
- 5. Longitudinal tachyons in Fermi–Dirac statistics
- 6. Conclusion
- Acknowledgements
- Appendix A. Equilibrium mechanics of superluminal fermionic modes
- References
1. Introduction
Superluminal radiation fields have never been properly quantized, despite of various attempts, most notably in [1, 2 and 3]. Here we carry out a purely statistical quantization, suggested by the very weak coupling of superluminal radiation to subluminal matter, some eleven orders below the electric fine structure constant. An elementary approach, avoiding propagators and field theoretical expansions, is quite sufficient to describe superluminal quantum effects such as the spontaneous emission of tachyons. The interaction of tachyonic quanta with matter will be settled by detailed balancing of emission and absorption rates, along Einstein's arguments, and the statistics of the superluminal modes will be determined by positivity requirements on energy.
The field theoretical second quantization of superluminal radiation has failed for two reasons. In a relativistic context, there is an insurmountable causality problem [4, 5, 6, 7, 8, 9, 10, 11 and 12], and one also quickly runs into a positivity problem with regard to energy, accompanied by a variety of inconsistencies, such as the violation of unitarity and unstable ground states. In this paper, we focus on the statistics of modes rather than fields, on spectral distributions rather than propagators, and interactions are settled by equilibrium balancing rather than renormalization. Instead of prescribing commutators or anticommutators for the wave function, our starting point will be the operator interpretation of the time-averaged energy functional. The algebraic relations between the Fourier modes are chosen in a way to turn the indefinite classical energy functional into a positive definite Hamiltonian. This is achieved by using commutators for transversal modes, and anticommutators for longitudinal ones. The transversal modes resemble photons with a negative mass-square, but the third degree of freedom is subjected to the exclusion principle, the longitudinal modes being fermions.
The crucial point is to use Bose as well as Fermi statistics for one and the same field. This is in fact very unusual, as second quantization in three space dimensions is customarily set up by an operator interpretation of the classical wave function. The statistics, either Bose or Fermi, is then determined by the spin-statistics theorem [13], which, however, only applies to subluminal fields. The quantization here carried out turns the superluminal radiation field into a mixture of transversal bosons and longitudinal fermions. The tachyonic spectral functions are gray-body Fermi and Bose distributions in quasi-equilibrium (due to the energy dissipation discussed below), with a negative mass-square in the dispersion relation. For equilibrium to be reached, one has to admit emission and absorption processes, so that the particle numbers cannot be prescribed, and accordingly there is no chemical potential, even not for the fermionic modes. Superluminal quanta couple by minimal substitution to subluminal matter, and transition rates will be obtained by detailed balancing.
Tachyon radiation cannot be understood in a relativistic context, because of causality violation [12], it requires an absolute space, tantamount to a medium of wave propagation. Hence, when discussing statistical distributions of superluminal quanta, we have to reckon with the substance of space, the ether [15]. The absorptivity of the ether results in energy dissipation affecting the spectral functions. Superluminal radiation is thus gray- rather than black-body, provided the dissipation is sufficiently adiabatic for equilibrium mechanics to be applicable. This depends on the permeability of the ether and can be made quite quantitative. The derivation of the energy distributions of the bosonic transversal modes and the longitudinal fermions is centered at the time-averaged energy-balance equation, a Poynting theorem in Fourier space, relating the field energy and the energy flux to the dissipated energy. The indefinite classical energy functionals (of field energy and dissipated energy) become positive definite operators by quantizing transversal and longitudinal modes in different statistics as mentioned. In the spectral distributions, the refractivity of the ether enters by the dispersion relation, and its absorptivity generates an adiabatic time variation of the temperature. As an example, we will discuss the cosmic tachyon radiation, in particular how equilibrium can be reached by interactions with subluminal matter.
In Section 2, the tachyonic counterpart to Maxwell's equations is introduced and all that goes with it, such as tachyonic field strengths, inductions, permeabilities and material equations, and the time-averaging of the superluminal energy flux is discussed. In Section 3, we study the energy-balance and the dissipation effected by the absorptivity of the ether. The statistical interpretation of the energy-balance equation is given in Section 4 for transversal and in Section 5 for longitudinal modes. We derive the spectral energy densities, the Einstein coefficients, the emission and absorption rates for bosonic and fermionic tachyons, as well as tachyonic ionization cross sections. In Section 6, we present our conclusions. In the appendix, we calculate the thermodynamic variables and the equations of state for the fermionic modes.
2. Tachyons in a permeable spacetime
Tachyons emerge as an extension of the photon concept, a sort
of photons with negative mass-square [15 and 16], satisfying
the Maxwell equations
Tachyonic E and B-fields relate to the vector potential by E=c−1(
 A0−∂A/t)
and B=rotA.
The inductive potential (C0,C)
enters via the tachyon mass and connects to the vector potential by
A0−∂A/t)
and B=rotA.
The inductive potential (C0,C)
enters via the tachyon mass and connects to the vector potential byThis complements the familiar material relations
where
 (t) and μ (t) denote the
dielectric and magnetic permeabilities, respectively. The tachyon mass mt
has the dimension of an inverse length, and is meant as a shortcut for mtc/
(t) and μ (t) denote the
dielectric and magnetic permeabilities, respectively. The tachyon mass mt
has the dimension of an inverse length, and is meant as a shortcut for mtc/ . The
signs of the mass terms in (2.1) are chosen
in a way that mt2>0
is the negative mass-square. We find mt/me≈1/238,
estimated from Lamb shifts in hydrogenic systems [17 and 18]. The tachyon
field couples by minimal substitution to subluminal matter. In the case
of a classical subluminal particle, the charge density and the current
in (2.1) read ρ=qδ(x−x(t))
and j=qvδ
(x−x (t)),
where q is the tachyonic charge carried by the
particle; quantized interactions will be discussed in 4 and 5. Tachyonic and
electric fine structure constants relate as q2/(4π
. The
signs of the mass terms in (2.1) are chosen
in a way that mt2>0
is the negative mass-square. We find mt/me≈1/238,
estimated from Lamb shifts in hydrogenic systems [17 and 18]. The tachyon
field couples by minimal substitution to subluminal matter. In the case
of a classical subluminal particle, the charge density and the current
in (2.1) read ρ=qδ(x−x(t))
and j=qvδ
(x−x (t)),
where q is the tachyonic charge carried by the
particle; quantized interactions will be discussed in 4 and 5. Tachyonic and
electric fine structure constants relate as q2/(4π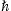 c)≈1.0×10−13≈0.66α6,
again an estimate from Lamb shifts. We will not consider
electromagnetic fields, so that we can use the notation so suggestive
in electrodynamics without the risk of confusion. The mass term breaks
the gauge invariance, and the tachyon potential (A0,A)
becomes observable, resulting in a new set of material equations and an
induction (C0,C).
In ((2.2) and (2.3)), one may
substitute
c)≈1.0×10−13≈0.66α6,
again an estimate from Lamb shifts. We will not consider
electromagnetic fields, so that we can use the notation so suggestive
in electrodynamics without the risk of confusion. The mass term breaks
the gauge invariance, and the tachyon potential (A0,A)
becomes observable, resulting in a new set of material equations and an
induction (C0,C).
In ((2.2) and (2.3)), one may
substitute  (t)=δ (t)+κ (t)
(δ stands for the Dirac function) and μ (t)=δ (t)+χ
(t), the susceptibilities κ (t)
and χ (t) are required to vanish identically for
negative t, as the response of the medium cannot
happen prior to its exposure to the field.
(t)=δ (t)+κ (t)
(δ stands for the Dirac function) and μ (t)=δ (t)+χ
(t), the susceptibilities κ (t)
and χ (t) are required to vanish identically for
negative t, as the response of the medium cannot
happen prior to its exposure to the field.
Defining the Poynting vector as S=cE×H+mt2A0C,
we obtain from the Maxwell equations and the material relations
 and μ are constant and j=0, we may write
divS+∂ρE/∂t=0,
with the indefinite density
and μ are constant and j=0, we may write
divS+∂ρE/∂t=0,
with the indefinite densityThe energy of the transversal and longitudinal modes can be
extracted from (2.4) by time
averaging. To this end, we turn to the plane wave decomposition of the
spatial component of the vector potential,
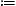 2πn/L. The summation is
over integer lattice points n in R3,
corresponding to periodic boundary conditions, so that the L−3/2
exp (ikx)
are orthogonal and complete in a box of size L. The
damping of plane waves is described by a complex frequency ω = ωR+iωI,
with ωI
2πn/L. The summation is
over integer lattice points n in R3,
corresponding to periodic boundary conditions, so that the L−3/2
exp (ikx)
are orthogonal and complete in a box of size L. The
damping of plane waves is described by a complex frequency ω = ωR+iωI,
with ωI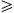 0, and ω*
denotes the complex conjugate. The amplitudes
0, and ω*
denotes the complex conjugate. The amplitudes  k,1
and
k,1
and  k,2
(linear polarization vectors) orthogonal to
k,2
(linear polarization vectors) orthogonal to  k,3
k,3
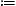 k0=k/|k|,
so that the
k0=k/|k|,
so that the  k,λ
constitute an orthonormal triad for every n.
The amplitudes â(k,λ) are complex numbers.
In (2.6) we depart
from the standard electromagnetic formalism in a permeable medium,
assuming a real wave vector k and an
exponential damping factor exp (−ωIt),
generated by a complex frequency. The amplitudes of the time component
of the real vector potential are defined as in (2.6) with
k,λ
constitute an orthonormal triad for every n.
The amplitudes â(k,λ) are complex numbers.
In (2.6) we depart
from the standard electromagnetic formalism in a permeable medium,
assuming a real wave vector k and an
exponential damping factor exp (−ωIt),
generated by a complex frequency. The amplitudes of the time component
of the real vector potential are defined as in (2.6) with The Maxwell equations (2.1) (with ρ=0, j=0)
read in Fourier space
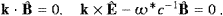
The Fourier coefficients of the field strengths and the vector potential relate as and
and the same for
(with real k
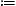 |k|) as well as the Lorentz condition,
|k|) as well as the Lorentz condition,must hold, which is also sufficient. As k2 in (2.9) is real, ω*(k)=ωR−iωI satisfies
the argument in the permeabilities is ω*, unless stated otherwise.
The vector potential can be split into a transversal and
longitudinal component, cf. ((2.6) and (2.10)),
where we used the dispersion relation (2.9). The inductions are then obtained from (2.12). Both the transversal and longitudinal components independently satisfy the field equations (2.7), with arbitrarily prescribed amplitudes â (k,λ), λ=1,2,3.
We consider time averages over a period of 2π/ωR;
on this scale the variation of exp (−ωIt)
is assumed adiabatic. It is also understood that ωR+iωI=ω(k)
solves the dispersion relation (2.9). We denote
by Ψ(x,t) and Φ(x,t)
any of the fields A,A0,E,
B, or the inductions (2.12), all
defined by series of type (2.6). ![]() and
and ![]() are the
corresponding Fourier coefficients, such as
are the
corresponding Fourier coefficients, such as ![]() , etc. The time average of the product
, etc. The time average of the product ![]() is readily
calculated as
is readily
calculated as
The same relations (2.15) hold for the averaged square of B (BL=0) and the inductions, cf. ((2.12), (2.13) and (2.14)), with
Relations of type (2.15) also apply to the vector potential and the induced potential, to their spatial components as well as A0 and C0, with (2.16) replaced by
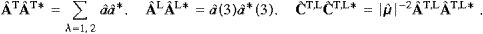
The argument in the permeabilities is ω*=ωR−iωI, and ω is a solution of the dispersion relation (2.9), so that (2.11) holds. As for the Poynting vector defined before (2.4), we find the spatially integrated and time averaged flux
The crucial point here is that the interference term of the transversal and longitudinal field components, cEL×H+mt2A0CT, has vanished in the averaging procedure, and we arrive at
The flow components can be made more explicit by ((2.13) and (2.14)),
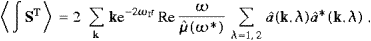
The meaning of this decomposition into a transversal and longitudinal flux will get apparent in the next section, when we discuss the corresponding splitting of the energy density and the energy dissipation in the ether.
3. Energy balance for superluminal radiation in a refractive and absorptive space–time
To identify the energy density of the transversal and
longitudinal modes as well as the dissipated energy, we derive at first
the time average of the conservation law (2.4), with the
external current dropped. We start with the E·∂D/∂t
term in (2.4), write
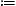 ωR−iωI,
ωR−iωI,which implies adiabatic damping compared to the harmonic time variation. We so find, by means of the time averaging defined after (2.14),
This also holds with the replacements
with the averaged energy density
and the same for the dissipated energy per unit time,
 ∫Idis
∫Idis , but
with
, but
with  ∫ρE
∫ρE with
the field energy, and
with
the field energy, and  ∫Idis
∫Idis with
the dissipated energy, but to do so we still have to disentangle the
transversal and longitudinal components like in (2.21).
with
the dissipated energy, but to do so we still have to disentangle the
transversal and longitudinal components like in (2.21).
The preceding time averages as well as the flux components (2.21) can be
further simplified by performing the ωI-expansion
in the dispersion relation (2.9). To this
end we assume ![]() , so that
, so that
In (3.8) the argument of the permeabilities is ωR, calculated via (3.7) as a function of k. The solution ω (k)=ωR+iωI of ((3.7) and (3.8)) also solves the dispersion relation (2.9) up to terms of O(ωI2), and we see from (3.8) that our assumption
up to O(ωI2). If not otherwise indicated,
In the averages  ∫ρE
∫ρE and
and  ∫Idis
∫Idis , cf.
(3.5), we rewrite
the products of the Fourier components by means of ((2.16), (2.17), (2.9) and (2.11)), and
then carry out the ωI-expansion as done in ((3.6), (3.7), (3.8) and (3.9)),
, cf.
(3.5), we rewrite
the products of the Fourier components by means of ((2.16), (2.17), (2.9) and (2.11)), and
then carry out the ωI-expansion as done in ((3.6), (3.7), (3.8) and (3.9)),
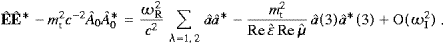
The λ-summations stem from the transversal components
 ∫ρE
∫ρE =
= ∫ρET
∫ρET +
+ ∫ρEL
∫ρEL and
and  ∫Idis
∫Idis =
= ∫IdisT
∫IdisT +
+ ∫IdisL
∫IdisL ,
where the transversal averages are
,
where the transversal averages are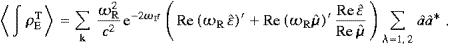
and the same holds for
 ∫ρEL
∫ρEL and
and  ∫IdisL
∫IdisL , but
with ωR2/c2
replaced by
, but
with ωR2/c2
replaced by  ∫ρET,L
∫ρET,L =O
(1),
=O
(1),  ∫ST,L
∫ST,L =O
(1), and
=O
(1), and  ∫IdisT,L
∫IdisT,L =O (ωI).
=O (ωI).
The positivity of the energy averages  ∫ρET
∫ρET and
and  ∫IdisT
∫IdisT is
ensured by requiring
is
ensured by requiring
 ∫ρEL
∫ρEL ,
,  ∫IdisL
∫IdisL , and
, and
 ∫SL
∫SL . The
transversal modes will be quantized in Bose statistics, which does not
affect the positivity of the transversal energy. In this way we will
obtain a positive definite Hamilton operator for the transversal as
well as longitudinal modes, so that we can identify
. The
transversal modes will be quantized in Bose statistics, which does not
affect the positivity of the transversal energy. In this way we will
obtain a positive definite Hamilton operator for the transversal as
well as longitudinal modes, so that we can identify  ∫ρE
∫ρE as
field energy, and
as
field energy, and  ∫Idis
∫Idis stands for the energy per unit time dissipated into the ether. The
conservation law (3.4) holds for
the transversal and longitudinal components individually.
stands for the energy per unit time dissipated into the ether. The
conservation law (3.4) holds for
the transversal and longitudinal components individually.
As a consistency check, we consider a single mode k
in the series ((3.9) and (3.11)), and
find, with vgr 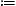 k0 dωR/dk,
k0 dωR/dk,
To prepare the second quantization in 4 and 5, we introduce
rescaled Fourier coefficients a (k,λ)
in the preceding time averages, so that â (k,λ)=:αTa
(k,λ) for λ=1,2, and â (k,3)=:αLa
(k,3), with the normalization
factors
so that the energy density in (3.11) gets a familiar shape,
The frequency
valid up to terms of O (ωI2) like (3.16). The energy per unit time dissipated by transversal and longitudinal modes is found as, cf. ((3.11) and (3.8)),
again up to O (ωI2).
As for the microscopic structure of the ether, we consider a
classical oscillator model [15], which gives
![]() and
and
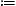 N0q02m0−1
and γ0>0. Here, ω0
is the free oscillator frequency, γ0 the damping
constant, N0 the number
density, m0 the mass, and q0
the tachyonic charge of the uniformly distributed oscillators
constituting the ether. We assume a narrow line breadth, γ0→0,
and real ω. The maximum of
N0q02m0−1
and γ0>0. Here, ω0
is the free oscillator frequency, γ0 the damping
constant, N0 the number
density, m0 the mass, and q0
the tachyonic charge of the uniformly distributed oscillators
constituting the ether. We assume a narrow line breadth, γ0→0,
and real ω. The maximum of 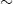 ω0. In the vicinity of the
resonance, we find the Lorentzian
ω0. In the vicinity of the
resonance, we find the LorentzianThe real part of
The Drude formula (3.19) is meant as a power series expansion in α0. As mentioned,
Accordingly, ωI(ωR) is uniformly α0-small in the whole frequency range. We will return to these limits when discussing tachyonic gray-body radiation, cf. (4.7), ωI determines the adiabatic time variation of the temperature in the spectral distributions.
4. Transversal tachyons in Bose-Einstein statistics
We quantize in occupation number representation. The Fourier
coefficients a (k,λ)
in the time averaged transversal energy density (3.16) are
replaced by operators ai,
and their complex conjugates a*(k,λ)
by the adjoints ai+.
Bose statistics is defined by the commutation relations [ai,aj+]=δij,
[ai,aj]=0
and [ai+,aj+]=0;
the indices i and j stand for
the modes (k,λ), k=2πn/L,
n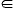 Z3,
λ=1,2, as defined after (2.6). Orthogonal
transversal states do not affect each other, and the longitudinal
degree of freedom can likewise be treated independently, cf. Section 5, as
operators in different orthogonal subspaces are supposed to commute.
Therefore, to save notation, we will drop the polarization index λ,
that is, quantize modes of a given linear polarization, λ=1, say.
Z3,
λ=1,2, as defined after (2.6). Orthogonal
transversal states do not affect each other, and the longitudinal
degree of freedom can likewise be treated independently, cf. Section 5, as
operators in different orthogonal subspaces are supposed to commute.
Therefore, to save notation, we will drop the polarization index λ,
that is, quantize modes of a given linear polarization, λ=1, say.
The number operators Ni
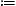 ai+ai
are Hermitian and commute. We consider the basis vectors |n1,…,ni,…,n∞
ai+ai
are Hermitian and commute. We consider the basis vectors |n1,…,ni,…,n∞ (shortcut |n
(shortcut |n ,
e.g. |0
,
e.g. |0 for
the vacuum state). The occupation numbers ni
are non-negative integers indicating the number of particles in state i.
In each basis vector, only a finite number of the ni
are non-zero. A scalar product is defined by
for
the vacuum state). The occupation numbers ni
are non-negative integers indicating the number of particles in state i.
In each basis vector, only a finite number of the ni
are non-zero. A scalar product is defined by  n|n′
n|n′ =δn1,n′1…δn∞,n′∞.
Operators satisfying the above commutation relations are readily found,
=δn1,n′1…δn∞,n′∞.
Operators satisfying the above commutation relations are readily found,
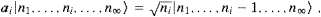
and ai|n
 =0
(zero-vector) if ni=0.
Hence,
=0
(zero-vector) if ni=0.
Hence,  ai+n|n′
ai+n|n′ =
= n|ain′
n|ain′ , as
well as Ni|n
, as
well as Ni|n =ni|n
=ni|n . We
so find the Hamilton operator of the
. We
so find the Hamilton operator of the  k,1-polarized
modes in (3.16) as
k,1-polarized
modes in (3.16) asand the same for the
 k,2-modes.
The partition function and the internal energy of modes of a given
transversal polarization is calculated in the usual way,
k,2-modes.
The partition function and the internal energy of modes of a given
transversal polarization is calculated in the usual way,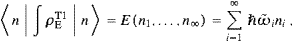
In the thermodynamic limit [20], ∑k→L3/(2π)3∫dk, we find
where
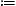 mtc/
mtc/ is
the smallest possible value of k:=|k|,
attained for ω=0 according to the dispersion relation (3.7). ωI
depends on k via ωR(k),
cf. (3.8). We will
frequently write ω for ωR, and replace in (3.7) mt
by mtc/
is
the smallest possible value of k:=|k|,
attained for ω=0 according to the dispersion relation (3.7). ωI
depends on k via ωR(k),
cf. (3.8). We will
frequently write ω for ωR, and replace in (3.7) mt
by mtc/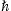 , see
after (2.3). To account
for two transversal degrees, we have to multiply log Z
as well as U by a factor of two, so that the
spectral and internal energy densities of transversal tachyonic
gray-body radiation read
, see
after (2.3). To account
for two transversal degrees, we have to multiply log Z
as well as U by a factor of two, so that the
spectral and internal energy densities of transversal tachyonic
gray-body radiation readk(ω) is defined in (3.7), and k′(ω)=dk/dω coincides with (3.13). We have here expanded (i.e., dropped) the damping factor exp (−2ωI(k)t) in the nominator of the integrand in (4.5), and in the denominator we have scaled this factor into the temperature variable, appealing to small ωI and adiabatic variation on time scales t
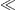 1/(2ωI),
otherwise the use of an equilibrium distribution would not be
justified. As pointed out in (3.22), one may
assume ωI(k) small in the
whole frequency range. The cosmic tachyon background also requires a
conformal time scaling of the temperature with the cosmic expansion
factor, β=a(t)/(kT).
1/(2ωI),
otherwise the use of an equilibrium distribution would not be
justified. As pointed out in (3.22), one may
assume ωI(k) small in the
whole frequency range. The cosmic tachyon background also requires a
conformal time scaling of the temperature with the cosmic expansion
factor, β=a(t)/(kT).
We derive some limit cases of the density (4.6), with
permeabilities as in (3.19). k(ω)
and k′(ω) are explicit in ((3.7) and (3.13)). In the
high frequency limit, we find k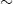 ω/c. For ω→0, we may
approximate k
ω/c. For ω→0, we may
approximate k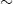 mt and k′
mt and k′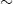 ωmt−1c−2(1+α0/ω02),
see after (3.21). Hence,
for high frequencies and with permeabilities as suggested in ((3.19), (3.20), (3.21) and (3.22)), ρT
(ω) converges to the Wien limit of the photonic Planck distribution,
and in the Rayleigh–Jeans limit we find a linear frequency scaling,
ωmt−1c−2(1+α0/ω02),
see after (3.21). Hence,
for high frequencies and with permeabilities as suggested in ((3.19), (3.20), (3.21) and (3.22)), ρT
(ω) converges to the Wien limit of the photonic Planck distribution,
and in the Rayleigh–Jeans limit we find a linear frequency scaling,
We turn to the coupling of the tachyon field to matter, and
study a subluminal, non-relativistic and spinless quantum particle
carrying tachyonic charge q. We start with the
Schrödinger equation for an attractive Coulomb potential V,
coupled by minimal substitution to the tachyon field,
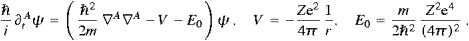
so that the tachyonic charge density in (2.1) reads ρ=qψ*ψ. If Aμ=0, we find the discrete hydrogen-like spectrum En=(1−1/n2)E0. The ionization energy E0 has been inserted in (4.9) to define a zero ground state energy E1. In this section we consider transversal fields AT, so that A0=0, cf. (2.13). The interaction Hamiltonian can be readily extracted from (4.9),
where we dropped terms quadratic in AT. The bound states of the unperturbed Coulomb problem are expanded as ψ=∑nbnune−iEnt/
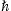 ,
with time-separated normalized eigenfunctions, ∫umun*
dx=δnm,
resulting in a bound state energy functional H(ψ)=∑nEnbn*bn.
As above, we substitute for the Fourier amplitudes bn
statistical operators, writing bn+
for the adjoint (instead of bn*).
These operators may satisfy Bose statistics as above, or, equally well,
the anticommutation relations of Fermi statistics, [bi,bj+]+=δij,
[bi,bj]+=0
and [bi+,bj+]+=0.
We will consider a single subluminal particle, and so the statistics
does not matter. The particle number operators Ni
,
with time-separated normalized eigenfunctions, ∫umun*
dx=δnm,
resulting in a bound state energy functional H(ψ)=∑nEnbn*bn.
As above, we substitute for the Fourier amplitudes bn
statistical operators, writing bn+
for the adjoint (instead of bn*).
These operators may satisfy Bose statistics as above, or, equally well,
the anticommutation relations of Fermi statistics, [bi,bj+]+=δij,
[bi,bj]+=0
and [bi+,bj+]+=0.
We will consider a single subluminal particle, and so the statistics
does not matter. The particle number operators Ni
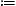 bi+bi
are in either case Hermitian and commute. As for the fermionic
occupation number representation, the ni
are restricted to 0 and 1, and the Fermi operators are defined by
bi+bi
are in either case Hermitian and commute. As for the fermionic
occupation number representation, the ni
are restricted to 0 and 1, and the Fermi operators are defined by =(−)n<ini|n1,…,1−ni,…,n∞
=(−)n<ini|n1,…,1−ni,…,n∞ ,
,with n<i
 ∑k=1i−1
nk, so
that the anticommutation relations are satisfied and Ni|n
∑k=1i−1
nk, so
that the anticommutation relations are satisfied and Ni|n =ni|n
=ni|n . It
is assumed that the statistical operators ak
of the tachyon field and their adjoints commute with the bi(+).
The interaction Hamiltonian (4.10) can be
represented in the tensorial product of the vector spaces used in ((4.1) and (4.11)). The
statistical operators are extended to the product space by bn(+)
. It
is assumed that the statistical operators ak
of the tachyon field and their adjoints commute with the bi(+).
The interaction Hamiltonian (4.10) can be
represented in the tensorial product of the vector spaces used in ((4.1) and (4.11)). The
statistical operators are extended to the product space by bn(+) id and id
id and id an(+),
so that these two sets commute.
an(+),
so that these two sets commute.
We study induced tachyon radiation and spontaneous emission of
tachyons, based on the interaction (4.10). The
initial and final states for absorption read
 abs=|0,…,1i,…,0j,…
abs=|0,…,1i,…,0j,…
 |n1,…,nk,…,n∞
|n1,…,nk,…,n∞ ,
,The first factor represents a single subluminal particle, and the second a set of tachyons distributed over some energy range. As for emission,
 em=|0,…,0i,…,1j,…
em=|0,…,0i,…,1j,…
 |n1,…,nk,…,n∞
|n1,…,nk,…,n∞ ,
,The first factor in ((4.12) and (4.13)) is a basis vector for Bose or Fermi statistics. In the second factor (bosonic), k=(k,λ) labels the tachyonic occupation number diminished or augmented when passing from the initial to the final state. As at the beginning of this section, we drop the index λ and consider a linearly polarized tachyon field, so that we can identify k with k in the subsequent summations.
We substitute the tachyonic and subluminal statistical
operators into the interaction Hamiltonian (4.10). The
transversal tachyonic wave operator of linear polarization λ is defined
by ((2.6) and (3.14)),
 in (4.10), we find
the interaction operator as
in (4.10), we find
the interaction operator asThe summation index k stands for k, and the polarization only enters via
 k,λ.
[In ((4.12) and (4.13)), the
indices i, j and k
are fixed and should not be confused with summation indices.] We so
find, cf. ((4.1), (4.11), (4.12), (4.13) and (4.15)),
k,λ.
[In ((4.12) and (4.13)), the
indices i, j and k
are fixed and should not be confused with summation indices.] We so
find, cf. ((4.1), (4.11), (4.12), (4.13) and (4.15)),These matrix elements are independent of the statistics used in defining bi(+), since the subluminal factors in (4.12) and (4.13) are one-particle states. nk is a tachyonic occupation number in Bose statistics.
The transition rate for induced absorption, with a given
linear polarization λ, is obtained by a standard procedure,
(The same formula also applies to transitions effected by longitudinal fermionic tachyons, cf. Section 5, so we do not indicate here the T-superscripts in wabsT,ind and TabsT.) For arbitrary real numbers ωE,I,
and we assume ωI
 0, t
0, t 1, ωIt
1, ωIt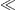 1,
so that F(ωE,ωI)
is strongly peaked as a function of ωE, with
maximum F(ωE≈0,ωI)≈t.
Due to dissipation, cf. Section 3,
energy conservation is only approximate, Re ωk≈ωj−ωi,
hence ωE≈0.
1,
so that F(ωE,ωI)
is strongly peaked as a function of ωE, with
maximum F(ωE≈0,ωI)≈t.
Due to dissipation, cf. Section 3,
energy conservation is only approximate, Re ωk≈ωj−ωi,
hence ωE≈0.
Like in ((4.4) and (4.5)), we
replace the box-summation in (4.18) by the
continuum limit
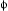 as solid
angle element. Explicit formulas for k(ωR)
and its derivative are given in (3.7) and (3.13). The ωR-integration
in (4.18) is then
carried out by steepest descent, at ωji
as solid
angle element. Explicit formulas for k(ωR)
and its derivative are given in (3.7) and (3.13). The ωR-integration
in (4.18) is then
carried out by steepest descent, at ωji
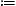 ωj−ωi,
ωj−ωi,ωI is by virtue of (3.8) a function of ωR, positive and uniformly bounded, cf. the end of Section 3, so that the restrictions mentioned after (4.21) are satisfied over the whole integration range. The steepest descent procedure boils down to (4.21); ωI is taken at ωR=ωji, likewise the remaining ωR-dependent factors in (4.18), and
The transition rate for emission is
 TemT
TemT |2,
contrary to the nk-proportionality
of |
|2,
contrary to the nk-proportionality
of | TabsT
TabsT |2,
cf. ((4.17) and (4.16)). We
split wemT
|2,
cf. ((4.17) and (4.16)). We
split wemT
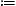 wemT,ind+wemT,sp,
where wemT,ind
denotes the contribution of the nk-proportional
terms in (4.24),
responsible for induced emission. A procedure completely analogous to
the foregoing gives
wemT,ind+wemT,sp,
where wemT,ind
denotes the contribution of the nk-proportional
terms in (4.24),
responsible for induced emission. A procedure completely analogous to
the foregoing giveswhere all factors outside the integral are taken at ωR=ωji=ωj−ωi as in (4.23), and αkT2 relates to dωR/dk as indicated after (3.14). Applying Green's formula, we recover the symmetry of Einstein's B-coefficients, BjiT(k,λ)=BijT(−k,λ). The transversal spontaneous emission rate wemT,sp is obtained by dropping the nk+1-factor of |
 TemT
TemT |2
in (4.24). The k-summation
in (4.24) is
replaced by the integration indicated after (4.4), and we
find, via ((4.20) and (4.21)),
|2
in (4.24). The k-summation
in (4.24) is
replaced by the integration indicated after (4.4), and we
find, via ((4.20) and (4.21)),The A- and B-coefficients for transversal tachyon radiation thus read
A consistency check of ((4.27) and (4.6)) is provided by the equilibrium balancing of emission and absorption events,
with occupation numbers related by their weight factors as
 k,λ·
k,λ·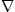 in ((4.23), (4.25) and (4.27)) by the
transversal component of the gradient,
in ((4.23), (4.25) and (4.27)) by the
transversal component of the gradient, 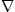 T
T 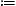
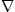 −k0(k0·
−k0(k0·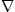 ).
).
In dipole approximation, we may drop the exponential e±ikx
in the preceding integrals and use the identity
 k,3,
as well as for unpolarized transversal radiation via the substitutions
k,3,
as well as for unpolarized transversal radiation via the substitutions  k,λ·
k,λ·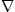 →
→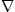 T and
T and  k,λ·dji→dji−k0(k0·dji).
As for the latter, the angular integration in ((4.23), (4.25) and (4.26)) can
easily be carried out with dji
as polar axis and ∫sin2θ dΩ=8π/3. We so find the
unpolarized total transversal transition rates as
k,λ·dji→dji−k0(k0·dji).
As for the latter, the angular integration in ((4.23), (4.25) and (4.26)) can
easily be carried out with dji
as polar axis and ∫sin2θ dΩ=8π/3. We so find the
unpolarized total transversal transition rates asThe detailed balancing condition (4.28) apparently also applies to A(T,d) and B(T,d), the Einstein coefficients in dipole approximation for unpolarized transversal radiation in all directions.
Finally we shortly discuss the tachyonic analog to the
photoelectric effect, the transfer of a bound electron into the
continuum by the absorption of a tachyon. The Coulomb wave functions of
the continuum are approximated by plane waves, that is, we put uj=L−3/2eikex
in the matrix element (4.16) (Born
approximation) to maintain the discrete states assumed in ((4.1) and (4.11)), and we
write u0 for the initial
bound state (not necessarily the ground state). In formula (4.18) for the
absorptive transition rate wabsind,
we take the k-summation over the electronic (rather
than tachyonic) wave vectors. (There is still only one electron, so
that the statistics used is irrelevant.) In the continuum limit, we may
replace this summation by
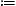 ωe−ω0−ωR(k).
Here, ω0,e are the frequencies of u0
and uj,
respectively, and k and ωk=ωR+iωI
refer to the tachyons. The dωe-integration is
carried out by steepest descent around ωe=ω0+ωR,
by making use of (4.21). Energy
conservation, ωE≈0, is again only approximate,
unless the dissipation generating ωI vanishes.
We so find
ωe−ω0−ωR(k).
Here, ω0,e are the frequencies of u0
and uj,
respectively, and k and ωk=ωR+iωI
refer to the tachyons. The dωe-integration is
carried out by steepest descent around ωe=ω0+ωR,
by making use of (4.21). Energy
conservation, ωE≈0, is again only approximate,
unless the dissipation generating ωI vanishes.
We so findThe integral can be replaced by
 k,λ·ke∫ei(k−ke)xu0
dx, the electronic ke
is taken at ωe≈ωR, cf. (4.32), as ωR
k,λ·ke∫ei(k−ke)xu0
dx, the electronic ke
is taken at ωe≈ωR, cf. (4.32), as ωR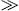 ω0 is required by the Born
approximation. The tachyonic k(ωR)
and ωI(ωR) are defined in
((3.7) and (3.8)), and the
amplitude αkT2
in (3.14). Dividing wabsT,ind
by the incoming tachyonic flux density, |vgr|nk/L3,
cf. (3.13), we find
the differential cross section for polarized transversal radiation,
ω0 is required by the Born
approximation. The tachyonic k(ωR)
and ωI(ωR) are defined in
((3.7) and (3.8)), and the
amplitude αkT2
in (3.14). Dividing wabsT,ind
by the incoming tachyonic flux density, |vgr|nk/L3,
cf. (3.13), we find
the differential cross section for polarized transversal radiation,The unpolarized transversal section is obtained by replacing |
 k,λ·ke|2
by
k,λ·ke|2
by 5. Longitudinal tachyons in Fermi–Dirac statistics
To render the longitudinal energy density in (3.16) positive,
we quantize the modes in Fermi statistics, cf. (4.11), otherwise
the reasoning is the same as in Section 4. Like
in (4.2), we replace
in the longitudinal density the Fourier coefficients by statistical
operators, and make use of the anticommutation relation [ai,aj+]+=δij,
which effects the sign change turning the energy density into a
positive definite operator,
In the thermodynamic limit, we find the spectral energy density and the internal energy of the longitudinal modes as, cf. ((4.5) and (4.6)),
Apparently, ρL differs from the transversal density ρT only by a sign change in the denominator and a factor of 1/2. (There is only one longitudinal degree of freedom.) As for the number density of the longitudinal modes, this is of course nL(ω)
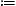 ρL(ω)/(
ρL(ω)/(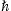 ω), so
that
ω), so
that 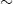 ρT/2, and the
Rayleigh–Jeans limit is quadratic in the frequency and temperature
independent,
ρT/2, and the
Rayleigh–Jeans limit is quadratic in the frequency and temperature
independent, Next, we calculate the Einstein coefficients for longitudinal
radiation. The interaction Hamiltonian is readily found, cf. ((4.9) and (4.10)),
and the time component follows from (2.13) via Â0(k)=α0LαLa(k,3) and the expansion ((3.6), (3.7) and (3.8)),
We also restore mt→mtc/
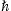 in k
and αL, cf. ((3.7) and (3.14)). Hence
we may write the interaction as
in k
and αL, cf. ((3.7) and (3.14)). Hence
we may write the interaction asThe operators a(+) are assumed in the representation (4.11). The b(+) of the subluminal particle may satisfy Bose or Fermi statistics, and we use for them the representations (4.1) or (4.11). The b(+) and a(+) commute. Thus we may take the initial and final states defined in ((4.12) and (4.13)), but the particle numbers ni in the second tensorial factor are now restricted to zero and one.
As for the absorption of a longitudinal fermionic tachyon,
with initial and final states defined in (4.12), we find
 f|HintL|i
f|HintL|i abs=
abs= TabsL
TabsL ei(ωj−ωi−ωk*)t
,
ei(ωj−ωi−ωk*)t
,and the matrix element for emission is likewise easily assembled from ((5.9), (4.13) and (4.11)),
 f|HintL|i
f|HintL|i em=
em= TemL
TemL e−i(ωj−ωi−ωk)t
,
e−i(ωj−ωi−ωk)t
,In either case, the nk only admit the values zero and one, and it is instructive to compare to the transversal bosonic radiation ((4.16) and (4.17)).
The transition rates can be compiled as in Section 4.
Equations ((4.18), (4.19), (4.20) and (4.21)) remain
unaltered, as well as (4.22), apart
from an obvious sign change in the denominator. We so find the induced
absorption rate for longitudinal fermionic quanta, cf. (5.10),
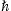 ωR
ωR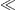 mc2,
as the subluminal particle is non-relativistic.
mc2,
as the subluminal particle is non-relativistic.
Concerning emission, the transition rate is determined by (4.24) with  TemL
TemL defined in (5.11). To keep
the formal analogy to the derivation following (4.24), we write
defined in (5.11). To keep
the formal analogy to the derivation following (4.24), we write ![]() , where −wemL,ind
stands for the contribution of the nk-proportional
terms in (5.11), and
, where −wemL,ind
stands for the contribution of the nk-proportional
terms in (5.11), and ![]() for the
remaining terms independent of nk.
The actual spontaneous emission rate wemL,sp
will be identified in (5.19). By
proceeding as after (4.24), we find
for the
remaining terms independent of nk.
The actual spontaneous emission rate wemL,sp
will be identified in (5.19). By
proceeding as after (4.24), we find
We restore the mass unit in αkL, that is, replace mt in (3.14) by mtc/
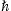 , and
so obtain
, and
so obtainIn this way we recover, via the balancing condition
the equilibrium distribution (5.4). In (5.22), we will write this balance in a more comprehensible form, with the proper A-coefficient.
The dipole approximation of the transition rates ((5.12), (5.13) and (5.14)) is
obtained by dropping the exponentials in the integrals, so that the
second integral in ((5.12), (5.13) and (5.15))
vanishes, and the first integral is settled by Ehrenfest's theorem (4.29). We so
find, in the same notation as in ((4.29), (4.30) and (4.31)), the
total (that is angular-integrated, ∫cos2 θ
dΩ=4π/3) longitudinal transition rates
with dji as defined in (4.29). Clearly, Bji(L,d)=Bij(L,d), and the first equality in (5.15) as well as the balancing conditions (5.16) are likewise evident in dipole approximation.
The spontaneous emission rate wemL,sp
and the Einstein A-coefficient attached to it are
readily identified,
It is clear from ((5.14) and (5.19)) that wemL,sp>0. Relations ((5.19), (5.20), (5.21) and (5.22)) also hold in dipole approximation, and we may compare to the transversal rates, cf. ((4.30) and (4.31)),
The transition rates derived in this section for longitudinal radiation in Fermi statistics are evidently quite similar to those for transversal radiation in Bose statistics discussed in Section 4; had we quantized the transversal tachyonic modes in Fermi–Dirac statistics, this would have only affected the transversal absorption rates by a factor
Next we derive the longitudinal ionization cross section, cf. ((4.32), (4.33) and (4.34)). The
same procedures as outlined after (4.31) lead to,
cf. ((4.33) and (5.12)),
The second term in the parentheses should be taken into account, despite ωR≈ωe
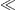 mc2/
mc2/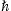 ,
since ke/k
,
since ke/k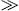 1 is possible and ωR
1 is possible and ωR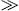 ω0 is needed for the plane
wave approximation. Also compare in this regard the discussion of the
maxima of the tansversal cross section in [14].
ω0 is needed for the plane
wave approximation. Also compare in this regard the discussion of the
maxima of the tansversal cross section in [14].
Next we discuss the equilibrium mechanics of longitudinal
tachyonic black-body radiation, ![]() , ωI=0; the thermodynamic formalism for the
superluminal transversal modes has already been studied in [14 and 18]. The peak of
the fermionic spectral density ρL(ω) in (5.5) depends on
the tachyon mass. Defining x
, ωI=0; the thermodynamic formalism for the
superluminal transversal modes has already been studied in [14 and 18]. The peak of
the fermionic spectral density ρL(ω) in (5.5) depends on
the tachyon mass. Defining x 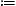 βhν and γ
βhν and γ 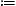 βmtc2,
we find the location of this peak by solving
βmtc2,
we find the location of this peak by solving
where αt/αe≈1.4×10−11 is the ratio of tachyonic and electric fine structure constants. Accordingly, at T≈2.725 K, we find wL/wT(νtL)≈1.45×10−14 and wT/wph(νtL)≈5.8×10−5, and comparable ratios for νtT and νph. Apparently, νtL also lies well within the core of the photon and transversal tachyon distributions. In the high-temperature limit, we find from (5.26) x(γ→0)≈3.131. The solution of (5.26) varies only moderately over the whole temperature range, and the same holds for the maximum of the transversal bosonic distribution, cf. [18]. A frequency defined by βhν0(T)=x≈2.218 lies for any temperature in the bulk of the enumerated distributions. Thus the location of the bulk of the spectral densities scales linearly with temperature, and Wien's displacement law is more or less recovered.
With these preparations, we can readily show that both the longitudinal and transversal quanta of the cosmic tachyon background have reached equilibrium at a rather early stage. Primordial nucleosynthesis requires a photonic equilibrium distribution at kT≈1 MeV, corresponding to a cosmic age of 1 s. At this temperature, we find hν0≈2.2 MeV, and the ratios wL/wT(ν0)≈2.6×105 and wT/wph(ν0)≈1.4×10−11. With increasing temperature, wL/wT gets quickly larger and overpowers wT/wph in their product. Thus one can assume that the longitudinal tachyon background has reached equilibrium within the first second, even before the photon background did, due to its stronger interaction with subluminal matter. As for the transversal tachyon radiation, this happened at a much later stage, but well within 1011 s (assuming a linear space expansion in this early epoch), the more so as wT/wph increases in time. In the present low-temperature regime, the ratios indicated after (5.27) hold, which makes the longitudinal fermionic radiation much harder to observe than the transversal boson background.
We turn to atoms in equilibrium with tachyon radiation. The dipole approximation (5.27) is the same for induced and spontaneous emission and absorption. We identify the Ly-α lines of hydrogen (10.2 eV) with the core frequency ν0 as defined above, corresponding to a temperature of kT(ν0)≈4.6 eV. We so find from (5.27) wL/wT(ν0)≈5.6×10−6 and wT/wph(ν0)≈3.0×10−9. The Ly-α1 transition in hydrogenic uranium (ν0≈0.23 MeV) results in a bulk temperature of kT(ν0)≈0.1 MeV. (At this temperature, the frequency ν0 lies in the core of the photonic and the two tachyonic spectral distributions.) In this case we find wL/wT(ν0)≈2.9×103, but a very small wT/wph(ν0)≈1.4×10−11. The chances to detect transversal tachyons improve in the low frequency fringe, due to the different frequency scaling of the photon and transversal tachyon distributions, cf. [18].
Finally we assemble the equations of state and the various
thermodynamic variables for the longitudinal fermionic quanta. The
subsequent high- and low-temperature expansions are derived in the
Appendix, cf. ((A.27) and (A.28)). For T→0,
we find in lowest order,
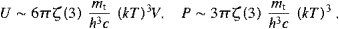
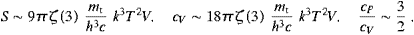
(We have dropped the subscript L.) The caloric and thermal equations get independent of the tachyon mass in this limit. The high-temperature limit reads in leading order
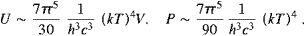
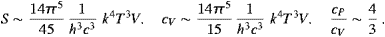
The tachyon mass does not enter in lowest order. The corresponding expansions for transversal tachyon radiation are very similarly structured, with moderately modified numerical constants [14], despite the different frequency scaling of the spectral densities in the Rayleigh–Jeans limit.
6. Conclusion
A new quantum statistics for superluminal radiation has been
suggested, resulting in a positive definite Hamiltonian and a stable
ground state. We have departed from the customary field theoretic
quantization, and chosen more elementary statistical procedures adapted
to the extremely small tachyonic fine structure constant, q2/(4π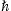 c)≈1.0×10−13.
The tiny coupling constant is key to the quantization of superluminal
radiation fields, this has been overlooked hitherto, as there have not
been quantitative estimates on the interaction strength of superluminal
radiation with matter. The weak interaction renders systematic quantum
field theoretic expansions academic, which are anyway marred by
negative energies and unstable vacua [1, 2 and 3]. In this
paper we have used detailed equilibrium balancing to describe the tiny
interaction of tachyons with subluminal matter.
c)≈1.0×10−13.
The tiny coupling constant is key to the quantization of superluminal
radiation fields, this has been overlooked hitherto, as there have not
been quantitative estimates on the interaction strength of superluminal
radiation with matter. The weak interaction renders systematic quantum
field theoretic expansions academic, which are anyway marred by
negative energies and unstable vacua [1, 2 and 3]. In this
paper we have used detailed equilibrium balancing to describe the tiny
interaction of tachyons with subluminal matter.
The statistical quantization developed here is completely self-consistent, and we have shown that it works, being capable of quantitative predictions based on realistic interactions, extremely weak but not out of reach. In the following I summarize the main features of superluminal quantum statistics. Tachyonic quantum ensembles are neither bosonic nor fermionic, they are a mixture of both. Statistics does not apply to the field, but to its modes, and in the case of superluminal radiation, we are not bound by the spin-statistics theorem, which requires the same algebraic relations for all modes. This freedom in the choice of the commutation relations for the Fourier amplitudes is used to render the energy density positive definite, ensuring a stable ground state. The superluminal quanta, transversal bosons and longitudinal fermions, admit gray-body spectra in quasi-equilibrium, with an adiabatic time variation of the temperature due to energy dissipation.
This energy dissipation relates to the underlying space structure. A consistent statistics of superluminal quanta cannot be achieved in a relativistic spacetime, due to causality violation manifested in advanced wave modes. Superluminal quanta need a very different context, a permeable space, the ether [15]. They interact with the refractive and absorptive ether, and this results in adiabatic energy dissipation. The starting point for quantization is the time averaged energy-balance equation, relating the superluminal energy flux to the field energy and the dissipated energy, cf. Section 3. This energy-balance is quantized by defining algebraic relations for the Fourier amplitudes. The statistics is chosen in a way to turn both the field energy and the dissipated energy into positive definite hermitian operators, transversal modes are bosons, longitudinal ones satisfy Fermi statistics, cf. 4 and 5. Once a positive definite Hamiltonian is established for the free superluminal modes, it is straightforward to balance emission and absorption rates, in this way arriving at Einstein coefficients which are adiabatically damped by the energy dissipation.
Spontaneous emission is in no way hampered by the exclusion principle, it applies to longitudinal fermionic quanta as well. The semiclassical arguments used in [14] are quite efficient to describe bosonic superluminal modes, but they also have their limits. The bosonic transition rates derived in second quantization ( Section 4) coincide with those of [14], provided we drop the adiabatic damping factors in the Einstein coefficients; the semiclassical derivation given in [14] does not account for the absorptivity of the ether and the resulting energy dissipation. Also, the exclusion principle is beyond semiclassical mechanics, and so we didn't attempt to study the longitudinal fermionic modes in [14]. The black-body limit of the fermionic equations of state is derived in the Appendix; the complete set of fermionic equilibrium variables is given in ((5.28) and (5.29)), complementing the variables for the transversal bosonic modes listed in (5.36) of [14].
In this paper we studied the equilibrium mechanics of superluminal quanta. We have not discussed applications, apart from some estimates on the cosmic tachyon background. But there are a variety of systems where one can try to spot quantum tachyons by means of the transition rates calculated in 4 and 5. Estimates of tachyonic ionization cross sections of Rydberg atoms are given in [14], the effect of tachyon radiation on Lamb shifts in hydrogenic systems and on hyperfine intervals is studied in [18]. Superluminal cyclotron radiation in planetary magnetospheres, and tachyonic synchrotron radiation and inverse Compton scattering in the magnetic fields of supernova remnants will be discussed elsewhere.
Acknowledgements
The author acknowledges the support of the Japan Society for the Promotion of Science. The hospitality and stimulating atmosphere of the Centre for Nonlinear Dynamics, Bharathidasan University, Trichy, the Institute of Mathematical Sciences, Madras, and the Tata Institute of Fundamental Research, Bombay, are likewise gratefully acknowledged. I would like to thank Nandor Balazs and George Contopoulos for exciting discussions.
References
Appendix A. Equilibrium mechanics of superluminal fermionic modes
We derive the high- and low-temperature expansions of the internal and free energy as well as the number density, based on the Fermi–Dirac spectral function (5.5) of the longitudinal modes in the black-body limit. The thermodynamic formalism for the transversal modes in Bose–Einstein statistics has already been worked out in [14], and the longitudinal modes do not really require new calculations but some reassembling.
We start with the internal energy, cf. (5.4) (with ![]() , ωI=0),
, ωI=0),
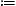 mtc2/(kT).
The asymptotic low-temperature limit is easily calculated via Watson's
Lemma, by replacing the root in (A.1) by its
series expansion,
mtc2/(kT).
The asymptotic low-temperature limit is easily calculated via Watson's
Lemma, by replacing the root in (A.1) by its
series expansion,In the high-temperature limit, a systematic convergent expansion of Û(α) is obtained by means of the Euler series (x<π)
We split the integral (A.1) into Û(α)=Û0+Û∞,
and choose α<δ<π. Series (A.3) converges absolutely in [0,δ]; we substitute it into Û0 and interchange summation and integration, arriving so at
The integrals in (A.5) represent hypergeometric functions [14], that is,
Finally we insert (A.6) into (A.5), and interchange summations, Û0(2)=Û0(2)odd+Û0(2)even,
The series in ((A.4), (A.5), (A.6), (A.7) and (A.8)) constitute the high-temperature expansion of the internal energy,
The coefficients in this expansion must be independent of δ, which can easily be checked by means of (A.4) and the integral representation of the cn(δ),
and similarly for n>2, with more terms subtracted. The series in ((A.4) and (A.7)) converge for α<π, which defines the convergence radius of the high-temperature expansion. I also remark, as an addendum to Eq. (4.19) of [14], where the internal energy of the transversal bosonic modes was studied, that
The free energy can be handled quite similarly,
The high-temperature expansion is again obtained by splitting the integral and expanding either nominator or denominator,
The integrals in (A.14) admit the expansion [14]
and by combining ((A.14) and (A.15)), we obtain
The coefficients cn(δ) are the same as in (A.8) and (A.10). [Apart from an integration constant,
We turn to the fermionic number density,
and the high-temperature limit is likewise found completely analogously to the foregoing. At first we write
and
The series expansion of the integrals in (A.21) is
ψ is the logarithmic derivative of the gamma function, elementary for (half-)integers. It enters here by a limit procedure, k→k+
 ,
needed to circumvent the poles in the hypergeometric functions defined
by the integrals, cf. [14]. Thus,
,
needed to circumvent the poles in the hypergeometric functions defined
by the integrals, cf. [14]. Thus, 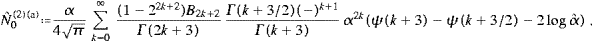
The coefficients (A.24) admit integral representations such as, cf. (A.10),
The high-temperature expansion of the particle density is thus, cf. ((A.20), (A.21) and (A.23)),
To summarize, we list the first two terms of the series
expansions derived in this Appendix. In the low-temperature limit, we
find from ((A.2), (A.12) and (A.19)),
All other fermionic variables, cf. ((5.28) and (5.29)), can be assembled from ((A.1), (A.11) and (A.18)).
 Fax:
+81-824-240717; email: roman@geminga.org
Fax:
+81-824-240717; email: roman@geminga.org