Tomaschitz, R. (1992). An alternative to wave mechanics on curved spaces, International Journal of Theoretical Physics 31, 187-210, DOI: 10.1007/BF00673252

 

 

Abstract (SpringerLink, CDS, SAO/NASA ADS, Zbl 0748.53026)

Geodesic motion in infinite spaces of constant negative curvature provides for the first time an example where a basically quantum mechanical quantity, a ground-state energy, is derived from Newtonian mechanics in a rigorous, nonsemiclassical way. The ground state energy emerges as the Hausdorff dimension of a quasi-self-similar curve at infinity of three-dimensional hyperbolic space H3 in which our manifolds are embedded and where their universal covers are realized. This curve is just the locus of the limit set Λ(Γ) of the Kleinian group Γ of covering transformations, which determines the bounded trajectories in the manifold; all of them lie in the quotient C(Λ)\Γ, C(Λ) being the hyperbolic convex hull of Λ(Γ). The three-dimensional hyperbolic manifolds we construct can be visualized as thickened surfaces, topological products I × S, I a finite open interval, the fibers S compact Riemann surfaces. We give a short derivation of the Patterson formula connecting the ground-state energy with the Hausdorff dimension δ of Λ, and give various examples for the calculation of δ from the tessellations of the boundary of H3, induced by the universal coverings of the manifolds.

 

 

Zbl 0748.53026
Tomaschitz, Roman
An alternative to wave mechanics on curved spaces
[J] Int. J. Theor. Phys. 31, No.2, 187-210 (1992). ISSN 0020-7748; ISSN 1572-9575

MSC 2000:

*53C22 Geodesics
57M05 Fundamental group, etc.
81Q99 General mathematical topics and methods in quantum theory

Keywords: geodesic motion; ground state energy; Patterson formula; Hausdorff dimension

 

Title:

 

An alternative to wave mechanics on curved spaces

Authors:

 

Tomaschitz, Roman

Affiliation:

 

AA(Instituts Internationaux de Physique et de Chimie Solvay, Université Libre de Bruxelles)

Publication:

 

International Journal of Theoretical Physics, Volume 31, Issue 2, pp.187-210

Publication Date:

 

02/1992

Origin:

 

SPRINGER

DOI:

 

10.1007/BF00673252

Bibliographic Code:

 

1992IJTP...31..187T

 

 

 

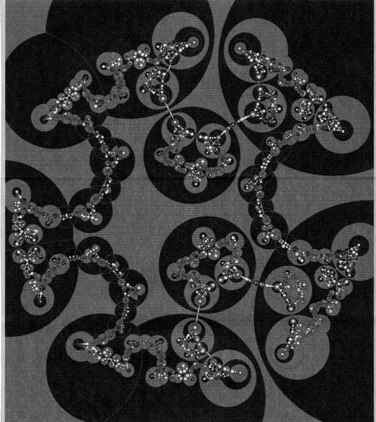
Fig.3. The faces of the polyhedra of the H3 tessellation lie on hemispheres placed on the circles. Every polyhedron also has two free faces at infinity, one in the interior, the other in the exterior of the Jordan curve (δ = 1.323), which are bounded by the same circles. The base circles and face-identifying mappings of the fundamental polyhedron F from which the tessellation originates (Section 3) are depicted in Figures 13 and 2. With this identification, F is topologically a thickened surface of genus five that inherits the metric of H3.

 

Fig.3. The faces of the polyhedra of the H3 tessellation lie on hemispheres placed on the circles. Every polyhedron also has two free faces at infinity, one in the interior, the other in the exterior of the Jordan curve (δ = 1.323), which are bounded by the same circles. The base circles and face-identifying mappings of the fundamental polyhedron F from which the tessellation originates (Section 3) are depicted in Figures 13 and 2. With this identification, F is topologically a thickened surface of genus five that inherits the metric of H3. full size image

 

 

  

Fig. 4. The fundamental polyhedron of this tessellation is a continuous deformation of that in Figure 3; the induced metric gives again a manifold whose fibers are surfaces of genus five, but which is nonisometric to that in Figure 3. The Hausdorff dimension δ of the Jordan curve, the set of accumulation points of the tiling, gives the ground-state energy of the Schrödinger operator on the manifold. δ = 1.307.

 

Fig. 4. The fundamental polyhedron of this tessellation is a continuous deformation of that in Figure 3; the induced metric gives again a manifold whose fibers are surfaces of genus five, but which is nonisometric to that in Figure 3. The Hausdorff dimension δ of the Jordan curve, the set of accumulation points of the tiling, gives the ground-state energy of the Schrödinger operator on the manifold. δ = 1.307. full size image

 

 

 

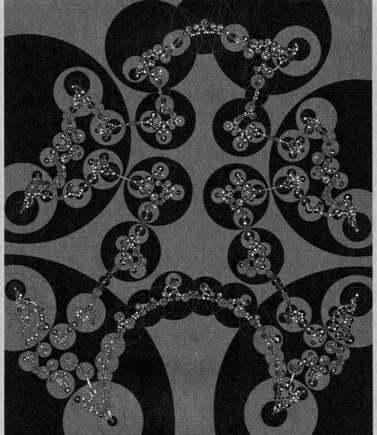
Fig. 6. As in Figure 3; the fibers are now surfaces of genus six corresponding to the identification pattern in Figures 5 and 12. Such tilings present simultaneous uniformizations of two Riemann surfaces (Bers, 1970), the boundary components of the manifold. δ = 1.312.

 

Fig. 6. As in Figure 3; the fibers are now surfaces of genus six corresponding to the identification pattern in Figures 5 and 12. Such tilings present simultaneous uniformizations of two Riemann surfaces (Bers, 1970), the boundary components of the manifold. δ = 1.312. full size image

  

 

Fig. 7. The interior of the Jordan curve in Figure 6. Quasiconformal deformations of the unit disk give rise to quasi-self-similar shapes; see the caption of Figure 9.

Fig. 7. The interior of the Jordan curve in Figure 6. Quasiconformal deformations of the unit disk give rise to quasi-self-similar shapes; see the caption of Figure 9. full size image

 

 

 

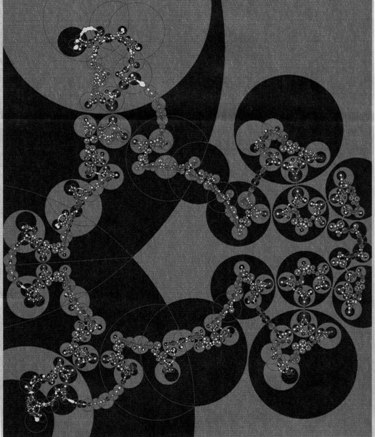
Fig. 8. Deformation spaces of hyperbolic manifolds are inhabited by many interesting species, their degree of differentiation depending on the genus of the fibers; here a tiling obtained by a deformation of the manifold in Figure 6. δ = 1.338.

 

Fig. 8. Deformation spaces of hyperbolic manifolds are inhabited by many interesting species, their degree of differentiation depending on the genus of the fibers; here a tiling obtained by a deformation of the manifold in Figure 6. δ = 1.338. full size image

 

 

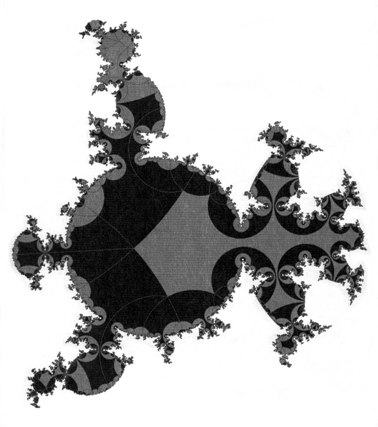
Fig. 9. The interior component of Figure 8. Every small piece of the boundary curve Λ(Γ) can be uniformly expanded to a standard size r0, and then mapped back into Λ(Γ) by a quasi-isometry Q (Ahlfors, 1966; McLaughlin, 1987; Sullivan, 1982),....as a measure for the deviation from self-similarity (K = 1).

Fig. 9. The interior component of Figure 8. Every small piece of the boundary curve Λ(Γ) can be uniformly expanded to a standard size r0, and then mapped back into Λ(Γ) by a quasi-isometry Q (Ahlfors, 1966; McLaughlin, 1987; Sullivan, 1982),....as a measure for the deviation from self-similarity (K = 1). full size image

 

 

description: Roman Tomaschitz (1992) An alternative to wave mechanics on curved spaces, International Journal of Theoretical Physics 31, 187.

 

Keywords: Laplace–Beltrami operator on open hyperbolic 3-manifolds, multiply connected topology, Poincaré series, hyperbolic spectral geometry, polyhedral tessellation of hyperbolic space, quasi-self-similar limit sets of Kleinian covering groups, quasi-Fuchsian groups, discrete subgroups of the Lorentz group, Möbius transformations in the Poincaré half-space, Jordan curves, Hausdorff measure and dimension, convex hull of a fractal limit set, universal covering projection, chaotic trajectories, Bernoulli property, Schrödinger equation, automorphic wave fields, Green’s function, ground state energy of quantum fields on open hyperbolic 3-manifolds, ground-state wave function, semiclassical mechanics, deformation spaces of fibered hyperbolic 3-manifolds

 

download full-text article (scanned PDF, 2.6 MB)

 

back to index1989-99