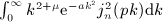We outline the systematic calculation of multiple antiderivatives 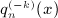 of the Legendre series qn(x) = Qn(1 + 2x2), see (4.3) and (4.9), as defined in (7.1). In particular, we derive the antiderivatives
of the Legendre series qn(x) = Qn(1 + 2x2), see (4.3) and (4.9), as defined in (7.1). In particular, we derive the antiderivatives 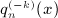 for k = 1,2,3,4, which are stated in (7.2), (7.5), (7.10), and (7.16).
for k = 1,2,3,4, which are stated in (7.2), (7.5), (7.10), and (7.16).
We start with some prerequisites relating to the geometric series
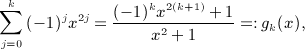 (A1)
(A1)
and its n-fold antiderivative
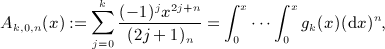 (A2)
(A2)
where we use the rising factorial (a)n = a(a + 1) ⋯ (a + n − 1) and (a)0 = 1. More generally, we will need the antiderivatives of gk(x)xl,
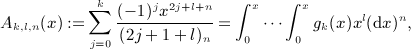 (A3)
(A3)
where k, l and n are nonnegative integers, and Ak,l,0(x) = gk(x)xl. We also note the identities
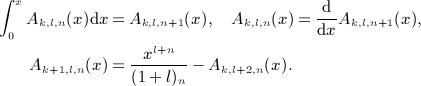 (A4)
(A4)
To assemble the antiderivatives  of the Legendre series (4.9), we need some integrals that can be expressed in terms of the finite series Ak,l,n(x) in (A3). First,
of the Legendre series (4.9), we need some integrals that can be expressed in terms of the finite series Ak,l,n(x) in (A3). First,
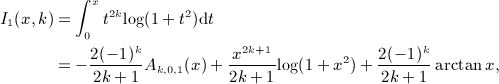 (A5)
(A5)
so that I ′ 1(x,k) = x2klog(1 + x2) = : I0(x,k). Odd powers can be dealt with in like manner,
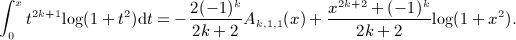 (A6)
(A6)
The integrals (A6) are needed to calculate the antiderivative of I1(x,k) in (A5),
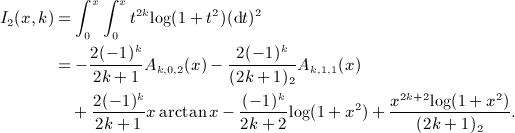 (A7)
(A7)
The third antiderivative of I0(x,k) reads
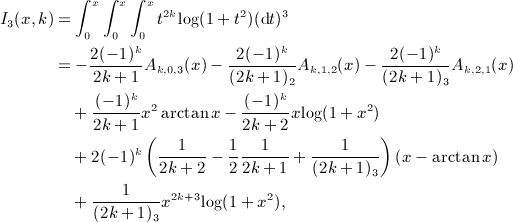 (A8)
(A8)
where we made use of identity Ak + 1,0,1(x) = x − Ak,2,1(x) in (A4).
The antiderivative of I3(x,k) is
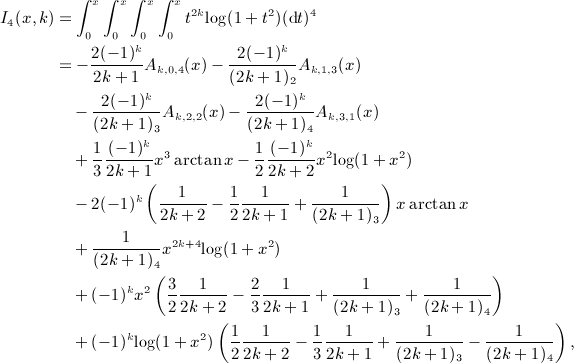 (A9)
(A9)
where we employed identity Ak + 1,1,1(x) = x2 / 2 − Ak,3,1(x), see (A4). In these iterative calculations,  , we used the elementary integrals
, we used the elementary integrals
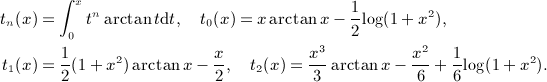 (A10)
(A10)
Apparently, I ′ n + 1(x,k) = In(x,k), which serves as a consistency check of the antiderivatives (A5) and (A7), (A8), (A9). When differentiating, we employ the differential identity in (A4) and make use of the fact that series Ak,l,0(x) can be summed in closed form as gk(x)xl, with gk(x) in (A1).
In addition to the integrals In(x,k), we need multiple antiderivatives of L0(x,k) = x2klogx, that is,
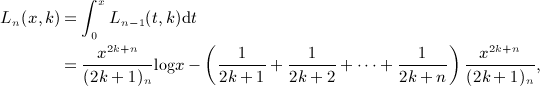 (A11)
(A11)
with n ≥ 1, as well as the antiderivatives of P0(x,k) = x2k,
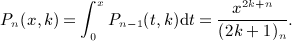 (A12)
(A12)
The i-fold antiderivatives 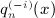 of the Legendre series qn(x), listed in Section 7 for i = 1,2,3,4, are assembled from the integrals In(x,k), Ln(x,k), and Pn(x,k), calculated in (A5), (A6), (A7), (A8), (A9), (A10), (A11), (A12). Substituting the Legendre series (4.9) into the multiple integral (7.1), we find
of the Legendre series qn(x), listed in Section 7 for i = 1,2,3,4, are assembled from the integrals In(x,k), Ln(x,k), and Pn(x,k), calculated in (A5), (A6), (A7), (A8), (A9), (A10), (A11), (A12). Substituting the Legendre series (4.9) into the multiple integral (7.1), we find
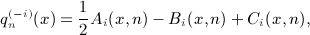 (A13)
(A13)
where
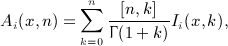 (A14)
(A14)
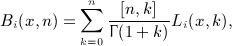 (A15)
(A15)
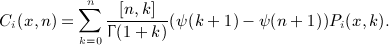 (A16)
(A16)
In series Ai(x,n), we interchange the k summation with the j summation of Ak,l,n(x) (defined in (A3) and occurring in the series representation of the integrals Ii(x,k)),
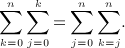 (A17)
(A17)
In the following, we list Ai(x,n) for i = 1,2,3,4. By making use of the antiderivative I1(x,k) in (A5) and the summation interchange (A17), we find, see (A14),
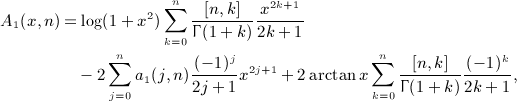 (A18)
(A18)
where the finite series a1(j,n) is stated in (7.3). The antiderivative 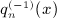 recorded in (7.2) is obtained by means of (A13) with (A15), (A16), and (A18) substituted.
recorded in (7.2) is obtained by means of (A13) with (A15), (A16), and (A18) substituted.
As for the second antiderivative 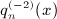 , see (A13), we obtain A2(x,n) in (A14) as
, see (A13), we obtain A2(x,n) in (A14) as
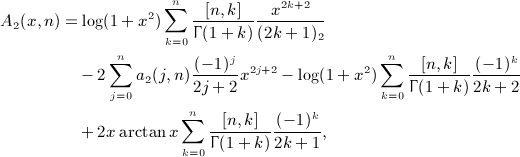 (A19)
(A19)
with series a2(j,n) defined in (7.6). Here, we used I2(x,k) in (A7) and interchanged summations according to the prescription (A17). The final result for 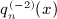 is stated in (7.5).
is stated in (7.5).
Regarding the calculation of 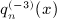 in (A.13), we can proceed analogously. Series A3(x,n) in (A14) is found by substituting integral I3(x,k), see (A8), and by performing the interchange (A17),
in (A.13), we can proceed analogously. Series A3(x,n) in (A14) is found by substituting integral I3(x,k), see (A8), and by performing the interchange (A17),
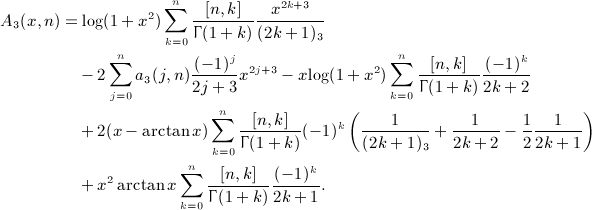 (A20)
(A20)
Series a3(j,n) is defined in (7.11), and the final result for 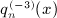 is recorded in (7.10).
is recorded in (7.10).
Finally, we substitute integral I4(x,n) (calculated in (A9)) into series A4(x,n) (defined in (A14)), and interchange summations as in (A17), to obtain
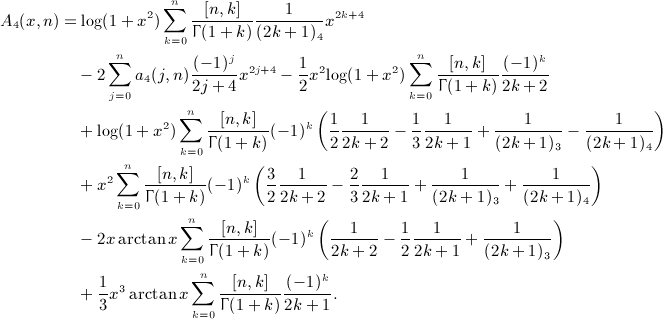 (A21)
(A21)
Series a4(j,n) is defined in (7.17). The fourth antiderivative 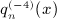 of the Legendre series (4.9) is assembled via (A13) by substitution of (A15), (A16), and (A21). The final result
of the Legendre series (4.9) is assembled via (A13) by substitution of (A15), (A16), and (A21). The final result 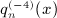 is stated in (7.16).
is stated in (7.16).
In (A18), (A19), (A20), (A21), we encounter series of type
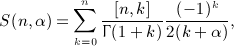 (A22)
(A22)
where Reα > 0, and the Hankel symbol [n,k] is defined in (2.4). All finite series arising in (A18), (A19), (A20), (A21), which do not involve powers of x, can be reduced to S(n,α) by partial fraction decomposition. Series (A22) can be traced back to the Legendre polynomial Pn(x) in representation (4.4), by performing a variable change x = 1 − 2y2,
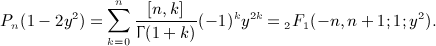 (A23)
(A23)
Thus, we may write series (A22) as
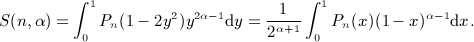 (A24)
(A24)
By making use of (A23) and a standard integral of the hypergeometric function [13], we find
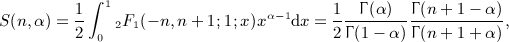 (A25)
(A25)
where n ≥ 0 is a nonnegative integer, and Reα > 0. In this way, we have summed series (A22). For instance,
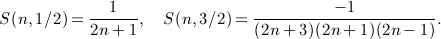 (A26)
(A26)
Singularities emerge in the gamma functions in (A25) at positive integer α. In this case, epsilon expansion is needed. We put α = m + ε, m ≥ 1, and use the expansion
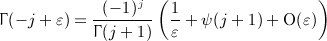 (A27)
(A27)
valid for integer j ≥ 0, where the psi function is defined in (4.7). We find S(n,m + ε) = O(ε) for n ≥ m and
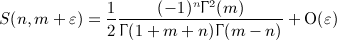 (A28)
(A28)
valid for n < m. Thus,
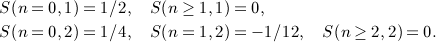 (A29)
(A29)
When assembling the antiderivatives 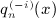 in Section 7, we make extensive use of series S(n,α) in (A22) for half-integer and integer α as listed in (A26) and (A29).
in Section 7, we make extensive use of series S(n,α) in (A22) for half-integer and integer α as listed in (A26) and (A29).
Finally we note a consistency check of the antiderivatives 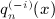 in (7.2), (7.5), (7.10), and (7.16). The numerical calculation of
in (7.2), (7.5), (7.10), and (7.16). The numerical calculation of 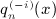 can directly be based on (A13), (A14), (A15), (A16), without the interchange of indices (A17) in Ai(x,n). That is, the coefficients Ai(x,n) required in (A13) are calculated by substituting the integrals Ii(x,k) into series (A14) and by performing the k summation as indicated in (A14). Closed analytic expressions of the integrals Ii(x,k) are given in (A5) and (A7), (A8), (A9), where we use the finite series representation (A3) of the antiderivatives Ak,l,n(x) in the numerical evaluation.
can directly be based on (A13), (A14), (A15), (A16), without the interchange of indices (A17) in Ai(x,n). That is, the coefficients Ai(x,n) required in (A13) are calculated by substituting the integrals Ii(x,k) into series (A14) and by performing the k summation as indicated in (A14). Closed analytic expressions of the integrals Ii(x,k) are given in (A5) and (A7), (A8), (A9), where we use the finite series representation (A3) of the antiderivatives Ak,l,n(x) in the numerical evaluation.
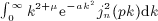 and Beltrami integrals
and Beltrami integrals 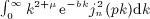 are studied, which arise in the multipole expansions of spherical
random fields. These integrals define spectral averages of squared
spherical Bessel functions
are studied, which arise in the multipole expansions of spherical
random fields. These integrals define spectral averages of squared
spherical Bessel functions 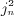 with Gaussian or exponentially cut power-law densities. Finite series
representations of the integrals are derived for integer power-law index
μ, which admit high-precision evaluation at low and moderate Bessel index n. At high n,
numerically tractable uniform asymptotic approximations are obtained on
the basis of the Debye expansion of modified spherical Bessel functions
in the case of Weber integrals. The high-n approximation of
Beltrami integrals can be reduced to Legendre asymptotics. The Airy
approximation of Weber and Beltrami integrals is derived as well, and
numerical tests are performed over a wide range of Bessel indices by
comparing the exact finite series expansions of the integrals with their
high-index asymptotics. Copyright © 2013 John Wiley & Sons, Ltd.
with Gaussian or exponentially cut power-law densities. Finite series
representations of the integrals are derived for integer power-law index
μ, which admit high-precision evaluation at low and moderate Bessel index n. At high n,
numerically tractable uniform asymptotic approximations are obtained on
the basis of the Debye expansion of modified spherical Bessel functions
in the case of Weber integrals. The high-n approximation of
Beltrami integrals can be reduced to Legendre asymptotics. The Airy
approximation of Weber and Beltrami integrals is derived as well, and
numerical tests are performed over a wide range of Bessel indices by
comparing the exact finite series expansions of the integrals with their
high-index asymptotics. Copyright © 2013 John Wiley & Sons, Ltd.


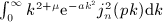
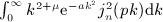 , that is squared spherical Bessel functions averaged with Gaussian power laws, as well as Beltrami integrals,
, that is squared spherical Bessel functions averaged with Gaussian power laws, as well as Beltrami integrals, 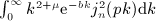 , where the average is performed with exponentially cut power laws at integer power-law exponent μ.
We derive finite series expansions of these integrals and also study
their high-index asymptotics, obtaining asymptotic approximations
suitable for numerical evaluation at high Bessel index n.
, where the average is performed with exponentially cut power laws at integer power-law exponent μ.
We derive finite series expansions of these integrals and also study
their high-index asymptotics, obtaining asymptotic approximations
suitable for numerical evaluation at high Bessel index n.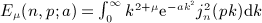 .
.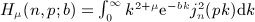 .
.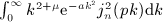
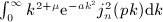
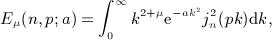
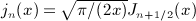
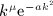 , Rea > 0, and p is a positive scale parameter. The Bessel index n is a nonnegative integer. For this integral to converge, the condition μ + 2 + 2n > − 1 has to be satisfied because jn(x) ∝ xn(1 + O(x2)) and jn(x) = O(1 / x). The factor k2 in the integrand typically stems from a volume integration
, Rea > 0, and p is a positive scale parameter. The Bessel index n is a nonnegative integer. For this integral to converge, the condition μ + 2 + 2n > − 1 has to be satisfied because jn(x) ∝ xn(1 + O(x2)) and jn(x) = O(1 / x). The factor k2 in the integrand typically stems from a volume integration 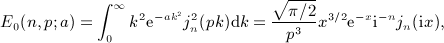
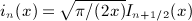 , which admits, for nonnegative integer index n, the finite series expansion
, which admits, for nonnegative integer index n, the finite series expansion 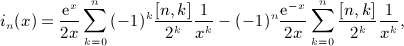
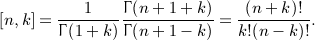
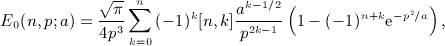
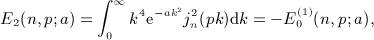
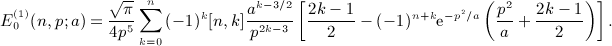
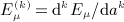 , with
, with 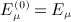 . Analogously, we find
. Analogously, we find 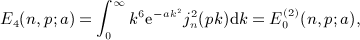
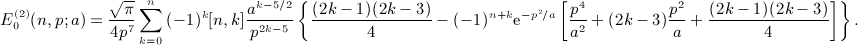
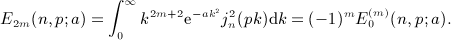
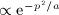 to find the asymptotic m-fold derivative of series
to find the asymptotic m-fold derivative of series 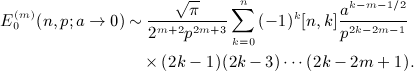
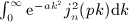
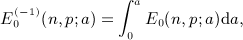
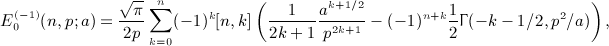
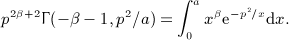
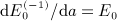 , which can readily be checked by way of the identity dΓ(α,y) / dy = − yα − 1e − y.
, which can readily be checked by way of the identity dΓ(α,y) / dy = − yα − 1e − y.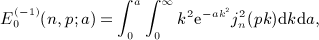
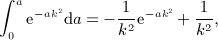
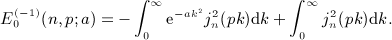
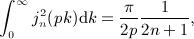
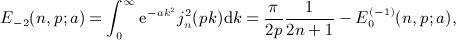
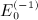 is the finite series
is the finite series 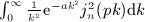
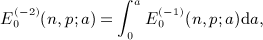
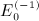 in
in 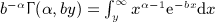 , as well as identity
, as well as identity 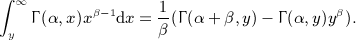
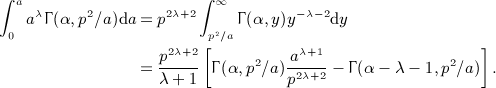
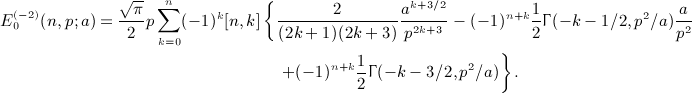
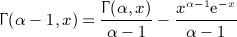
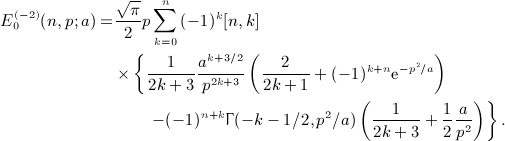
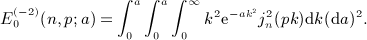
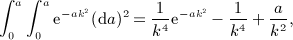
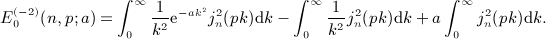
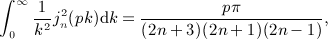
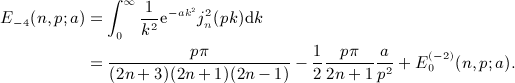
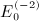 is stated in
is stated in 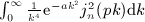
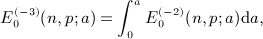
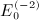 . The term-by-term integration is carried out by means of identity
. The term-by-term integration is carried out by means of identity 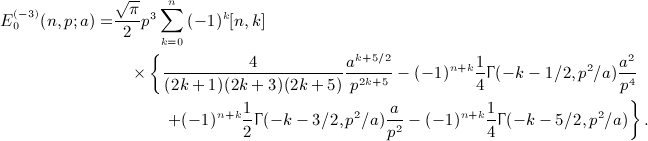
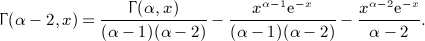
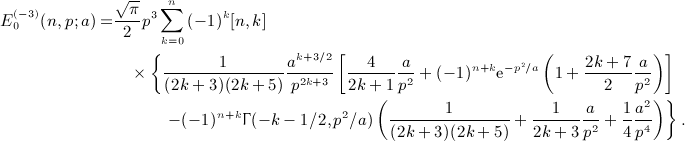
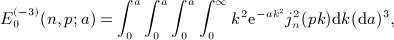
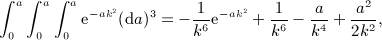
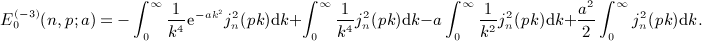
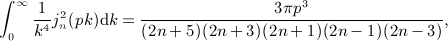
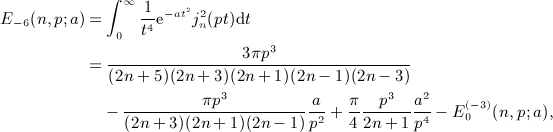
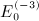 is the finite series calculated in
is the finite series calculated in 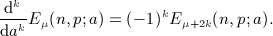
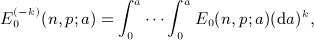
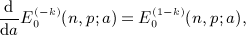
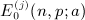 calculated for j = 2 in
calculated for j = 2 in 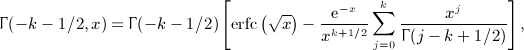
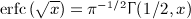 .
.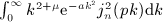
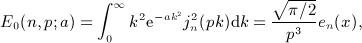
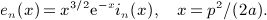
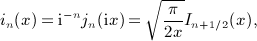
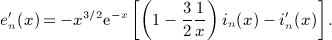
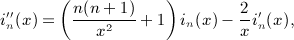
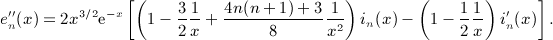
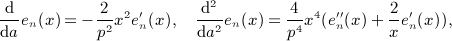
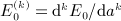 of Weber's integral
of Weber's integral 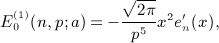
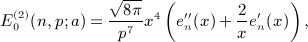
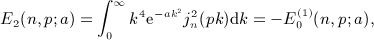
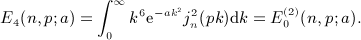
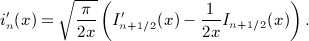
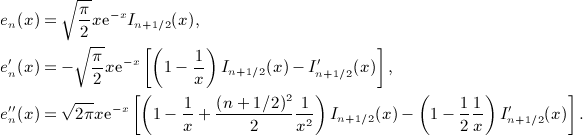
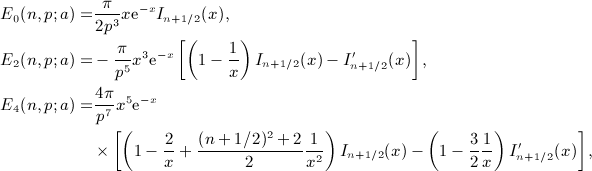
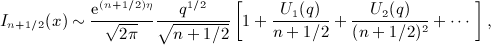
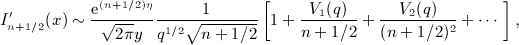
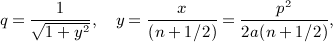
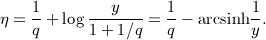
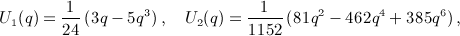
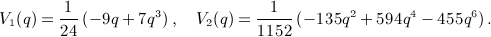
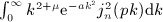
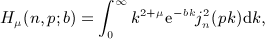
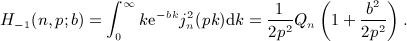
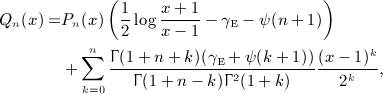
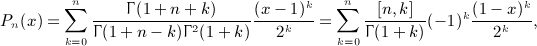
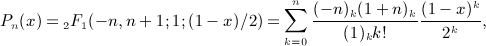
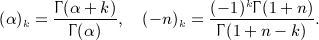
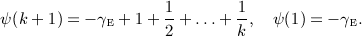
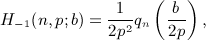
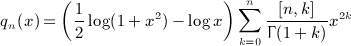
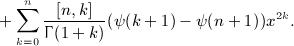
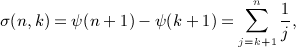
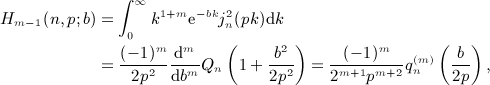
 ,
, 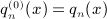 , and x = b / (2p).
, and x = b / (2p).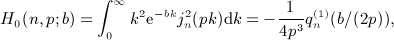
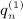 is the first derivative of qn(x) in
is the first derivative of qn(x) in 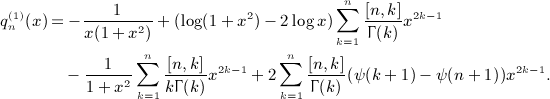
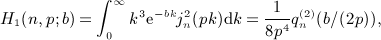
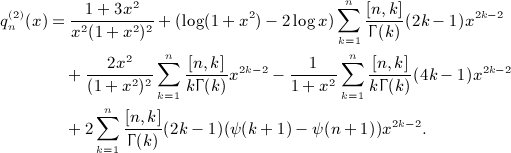
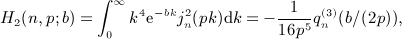
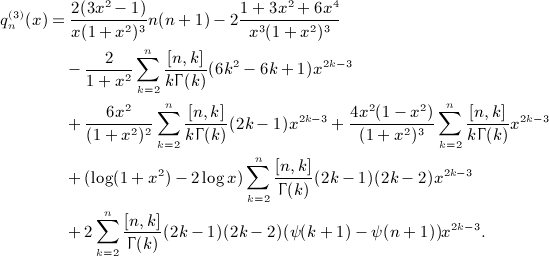
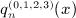 in
in 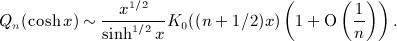
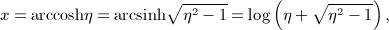
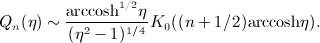
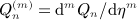 ,
, 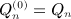 , reads, in leading order in n,
, reads, in leading order in n, 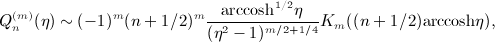
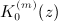 by ( − 1)mKm(z) to arrive at
by ( − 1)mKm(z) to arrive at 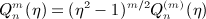 is an associated Legendre function of the second kind, of integer degree n and order m, with interval [ − 1,1] as branch cut
is an associated Legendre function of the second kind, of integer degree n and order m, with interval [ − 1,1] as branch cut 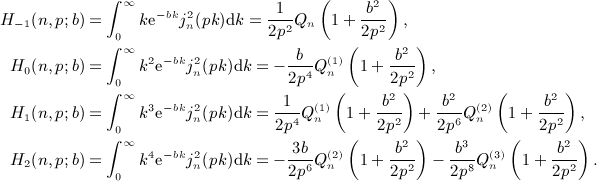
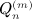 as stated in
as stated in 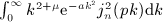
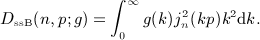
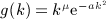 . Beltrami integrals Hμ(n,p; b) are defined by g(k) = kμe − bk, see
. Beltrami integrals Hμ(n,p; b) are defined by g(k) = kμe − bk, see 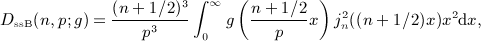
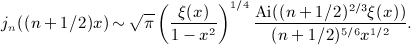
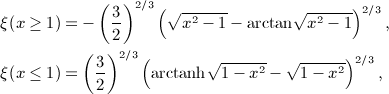
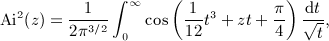
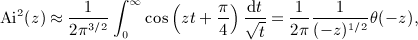
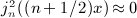 in the interval 0 < x < 1, where ξ(x) is positive, which means to replace the lower integration boundary in integral
in the interval 0 < x < 1, where ξ(x) is positive, which means to replace the lower integration boundary in integral 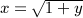 , and substitute
, and substitute 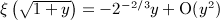 , to obtain
, to obtain 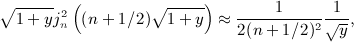
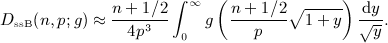
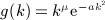 in
in 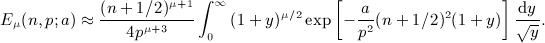
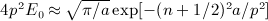 . This is just the leading order of the Debye expansion
. This is just the leading order of the Debye expansion 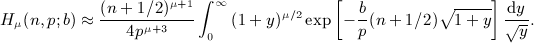
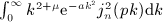
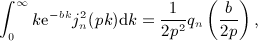
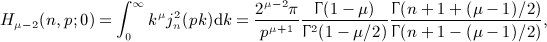
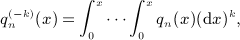
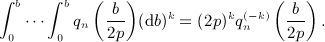
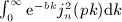
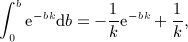
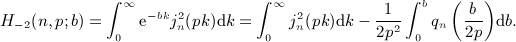
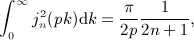
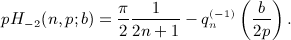
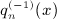 is defined in
is defined in 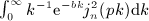
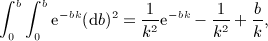
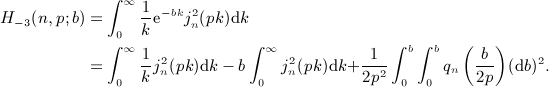
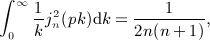
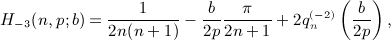
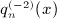 of the Legendre series
of the Legendre series 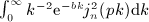
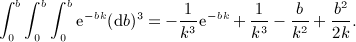
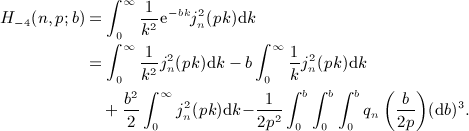
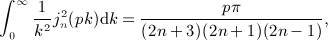
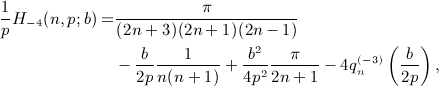
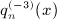 of
of 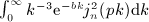
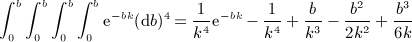
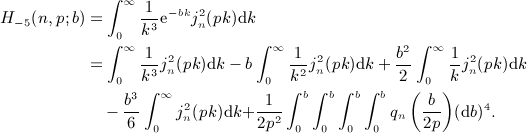
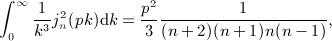
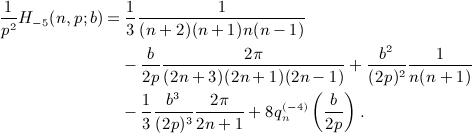
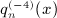 is composed of finite series and elementary functions and explicitly given in
is composed of finite series and elementary functions and explicitly given in 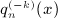 in
in 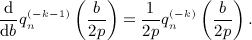
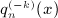 , stated in
, stated in 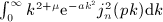
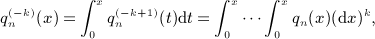
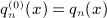 ,
, 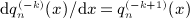 . We will also use the Hankel symbol [n,k] defined in
. We will also use the Hankel symbol [n,k] defined in 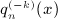 for k = 1,2,3,4, which completes the calculation of the Beltrami integrals
for k = 1,2,3,4, which completes the calculation of the Beltrami integrals 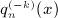 as finite linear combinations of elementary functions. In this section, we merely state the results.
as finite linear combinations of elementary functions. In this section, we merely state the results.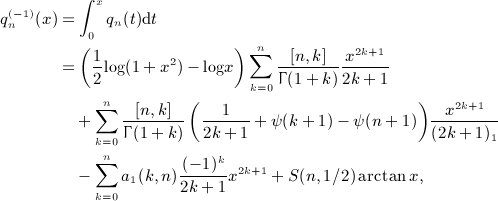
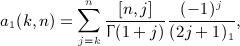
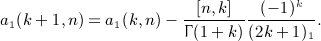
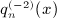 , obtained by integration of
, obtained by integration of 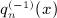 in
in 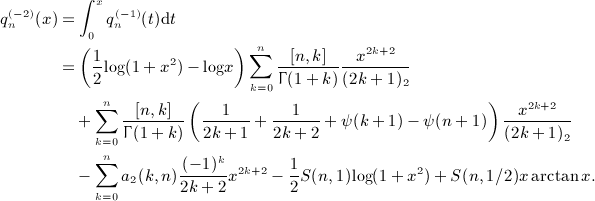
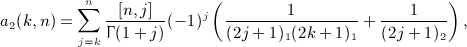
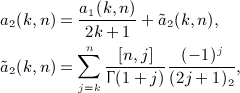
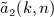 in
in 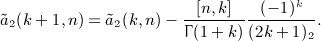
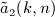 into partial fractions,
into partial fractions, 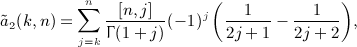
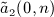 can be summed as
can be summed as 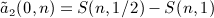 , see
, see 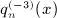 , obtained by integration of
, obtained by integration of 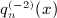 in
in 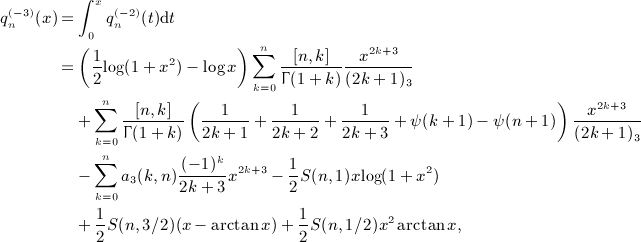
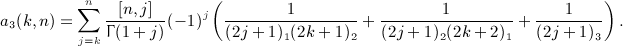
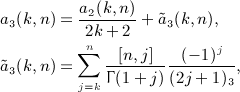
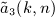 satisfies the recursive identity, see
satisfies the recursive identity, see 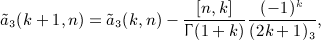
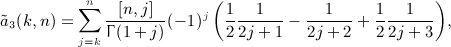
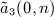 can be summed as, see
can be summed as, see 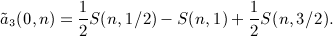
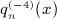 is found by integrating
is found by integrating 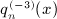 in
in 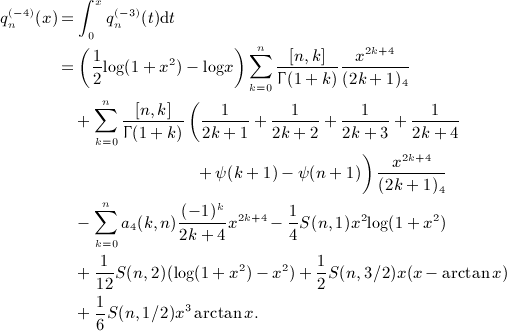
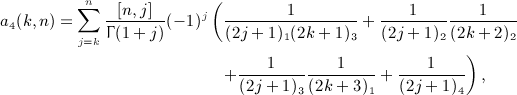
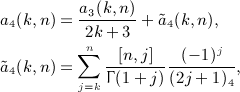
 in
in 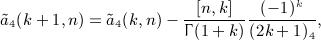
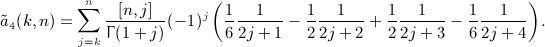
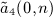 can be summed by means of
can be summed by means of 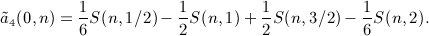
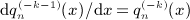 , k = 1,2,3, which can be checked by making use of the indicated properties of the series coefficients ai(k,n), see
, k = 1,2,3, which can be checked by making use of the indicated properties of the series coefficients ai(k,n), see 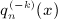 , k ≥ 1, defined in
, k ≥ 1, defined in 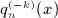 of the Legendre series
of the Legendre series 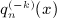 only in the open half-plane Rex > 0 because x = b / (2p), Reb > 0, and p > 0, see
only in the open half-plane Rex > 0 because x = b / (2p), Reb > 0, and p > 0, see 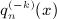 , k = 1, ⋯ ,4, given in
, k = 1, ⋯ ,4, given in 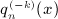 are obtained by comparing the finite series representation of H − k − 1(n,p; b), k = 1, ⋯ ,4, in
are obtained by comparing the finite series representation of H − k − 1(n,p; b), k = 1, ⋯ ,4, in 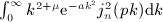
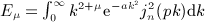 and Beltrami integrals
and Beltrami integrals 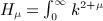
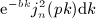 ,
and tested them by comparison with high-index asymptotic expansions.
These integrals arise in the multipole expansion of temperature
fluctuations of the cosmic background radiation, where multipoles up to
order n ≈ 104 can be resolved. In the integrands, a and b are exponents with positive real part, and p
is a positive scale parameter, which can be scaled out of the squared
spherical Bessel function by rescaling the exponents, so that we use p = 1 in the tables. μ is an integer power-law exponent and n ≥ 0 the integer Bessel index. The real parts of the exponents a and b are usually small in multipole expansions, see Tables
,
and tested them by comparison with high-index asymptotic expansions.
These integrals arise in the multipole expansion of temperature
fluctuations of the cosmic background radiation, where multipoles up to
order n ≈ 104 can be resolved. In the integrands, a and b are exponents with positive real part, and p
is a positive scale parameter, which can be scaled out of the squared
spherical Bessel function by rescaling the exponents, so that we use p = 1 in the tables. μ is an integer power-law exponent and n ≥ 0 the integer Bessel index. The real parts of the exponents a and b are usually small in multipole expansions, see Tables 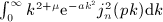
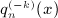 of the Legendre series qn(x) = Qn(1 + 2x2), see
of the Legendre series qn(x) = Qn(1 + 2x2), see 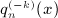 for k = 1,2,3,4, which are stated in
for k = 1,2,3,4, which are stated in 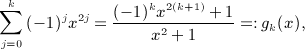
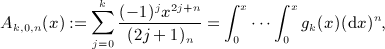
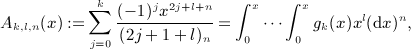
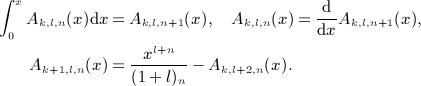
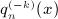 of the Legendre series
of the Legendre series 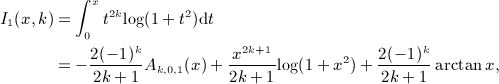
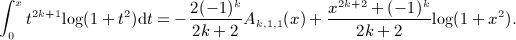
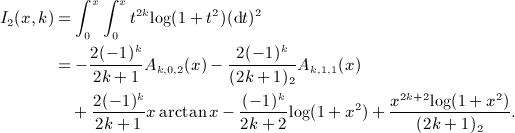
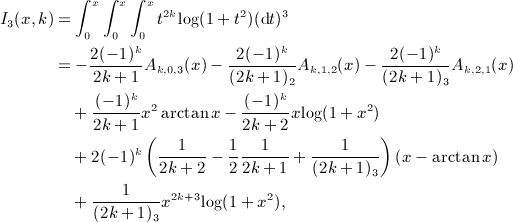
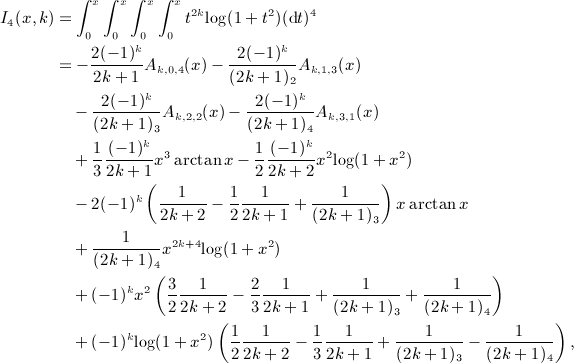
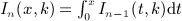 , we used the elementary integrals
, we used the elementary integrals 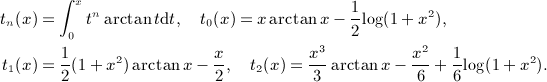
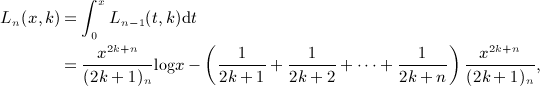
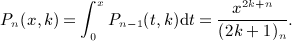
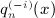 of the Legendre series qn(x), listed in
of the Legendre series qn(x), listed in 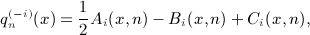
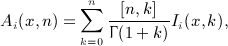
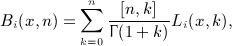
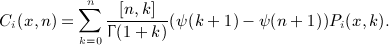
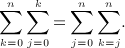
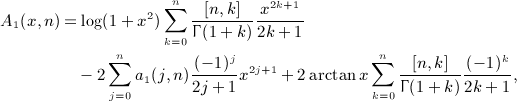
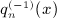 recorded in
recorded in 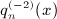 , see
, see 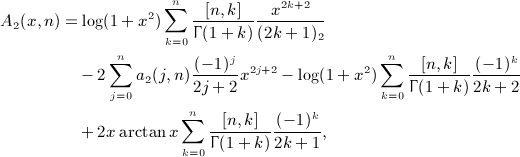
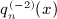 is stated in
is stated in 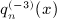 in (A.13), we can proceed analogously. Series A3(x,n) in
in (A.13), we can proceed analogously. Series A3(x,n) in 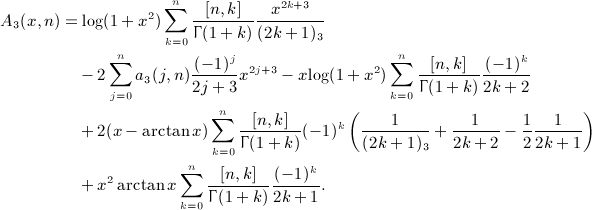
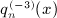 is recorded in
is recorded in 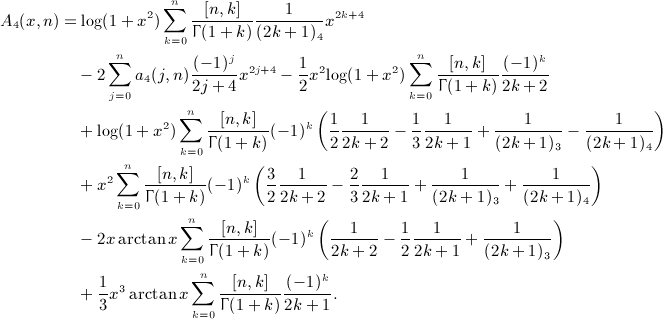
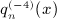 of the Legendre series
of the Legendre series 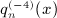 is stated in
is stated in 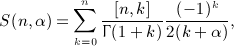
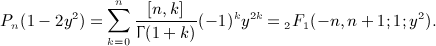
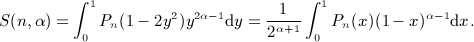
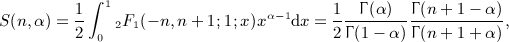
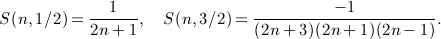
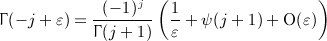
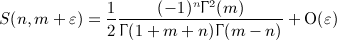
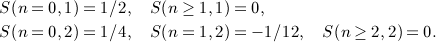
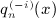 in
in 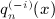 in
in 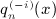 can directly be based on
can directly be based on