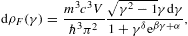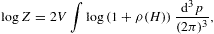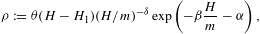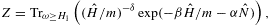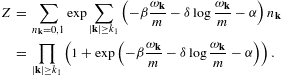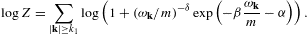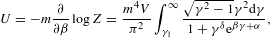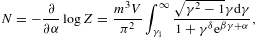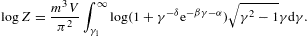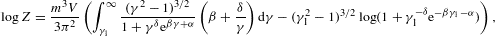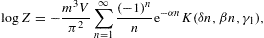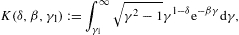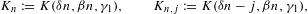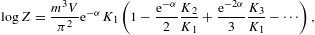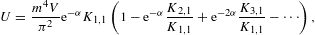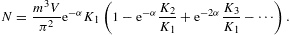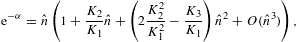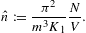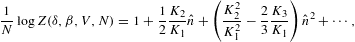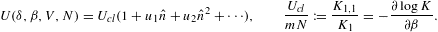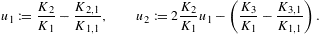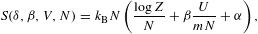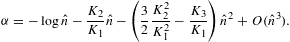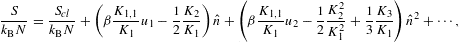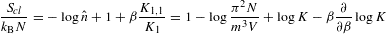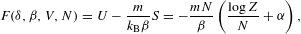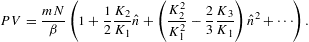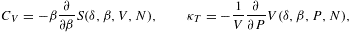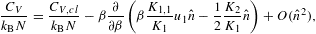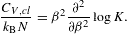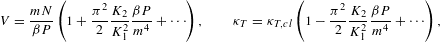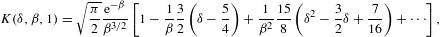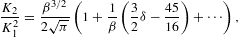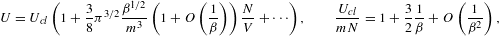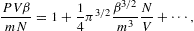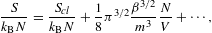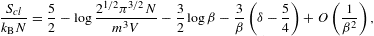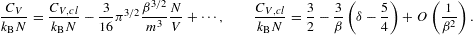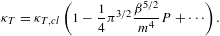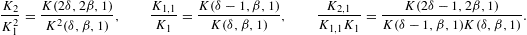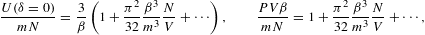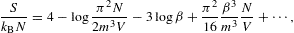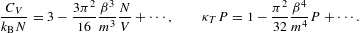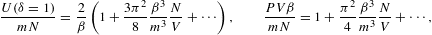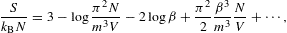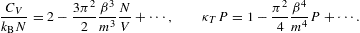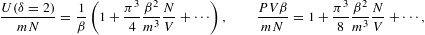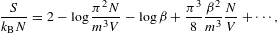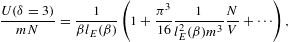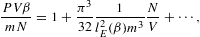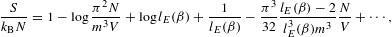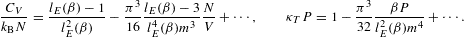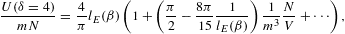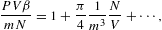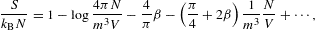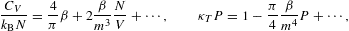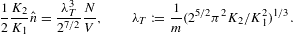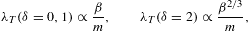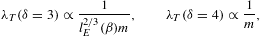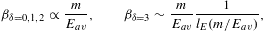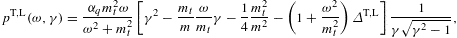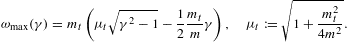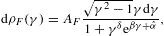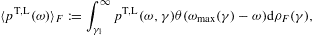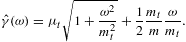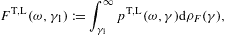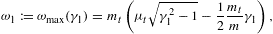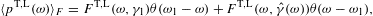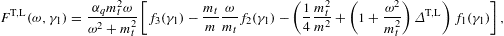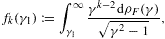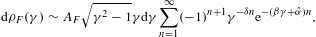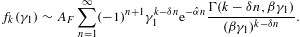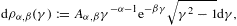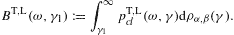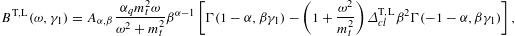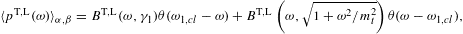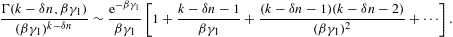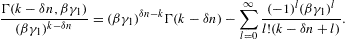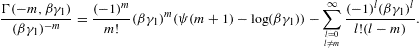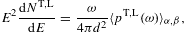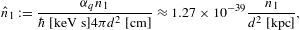Volume 387, Issue 14, 1 June 2008, Pages 3480-3494
Roman
Tomaschitz ,
a,
,
a,

Abstract
Fermionic power-law distributions are derived by the second quantization of classical power-law ensembles, and applied to ultra-relativistic electron populations in the Galactic center. The γ-ray flux from the direction of the compact central source Sagittarius A* is fitted with a superluminal cascade spectrum. In this way, estimates of the radiating electron plasma in the Galactic center region are obtained, such as the power-law index, temperature, particle number, and internal energy. The spectral averaging of the tachyonic radiation densities with Fermi power-laws is explained. Fugacity expansions of the thermodynamic variables (thermal equation of state, entropy, isochoric heat capacity, and isothermal compressibility) are obtained in the quasiclassical high-temperature/low-density regime, where the spectral fit is carried out. The leading quantum correction to these variables is calculated, and its dependence on the electronic power-law index and the thermal wavelength is discussed. Excess counts of cosmic rays from the Galactic center region are related to the plasma temperature inferred from the cascade fit.
Keywords: Superluminal radiation; Tachyonic cascade spectra; Fermi power-law ensembles; Ultra-relativistic electron plasma; Quasiclassical fugacity expansion; Spectral averaging
PACS classification codes: 05.30.Fk; 05.70.Ce; 52.25.Kn; 95.30.Tg
Article Outline
- 1. Introduction
- 2. Thermodynamic variables of Fermi power-law ensembles
- 3. Equations of state, entropy, and heat capacity of fermionic power-law densities in the quasiclassical regime
- 3.1. Low-temperature asymptotics
- 3.2. Fugacity expansion and thermal wavelength in the high-temperature limit
- 4. Superluminal γ-rays from the Galactic center: Tachyonic spectral maps and electronic source distributions
- 5. Conclusion
- Acknowledgements
- References
1. Introduction
Electronic power-law distributions are commonly used in electromagnetic spectral averages to model the synchrotron emission of astrophysical sources, such as the X-ray spectra of supernova remnants [1]. In this article, we quantize Boltzmann power-law densities, exponentially cut power-law distributionswhere the momentum integration has been parametrized with the electronic Lorentz factor γ. δ is the power-law index, and we use the shortcuts
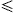 δ
δ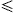 4.
4.
Here, we give evidence for superluminal radiation from the Galactic center by fitting recently obtained spectral maps [7], [8] and [9] with tachyonic cascade spectra. The tachyonic γ-ray wideband consists of two cascades generated by ultra-relativistic electron populations, and the spectral fit allows us to infer the thermodynamic parameters. The observed spectra are clearly distinguishable from electromagnetic synchrotron and inverse-Compton fits, due to the emergence of extended spectral plateaus. We show that the TeV spectral map of the Galactic center admits a tachyonic extension into the GeV region, providing an excellent fit to the spectrum of the unidentified γ-ray source 3EG J1746 − 2851 [10] associated with the Galactic central source Sagittarius A*. The superluminal cascades are generated by an ultra-relativistic electron gas at high temperature and low density, so that we can use distribution (1.1) in the quasiclassical regime to calculate the thermodynamic variables and the spectral averages.
In Section 2, we set up the thermodynamic formalism of fermionic power-law densities (1.1). Starting with the grand partition function, we derive the quasiclassical fugacity expansion of the thermodynamic variables, such as the caloric and thermal equations of state, entropy, specific heat, and compressibility. In Section 3, we discuss the leading quantum correction to the classical thermodynamic functions. In the high-temperature regime, the quantum corrections become more pronounced with increasing electronic power-law index, exhibiting the same temperature scaling as the classical limit usually dominant in the high-temperature/low-density regime. This is illustrated by calculating the mentioned variables for an increasing sequence of electron indices. We study the thermal wavelength of fermionic power-law ensembles in the low- and high-temperature regime, and discuss the range of applicability of the quasiclassical fugacity expansion.
In Section 4, we average
the quantized superluminal radiation densities with the power-law
distributions (1.1), and
derive the fugacity expansion of the spectral averages. We perform a
tachyonic cascade fit to the γ-ray
spectrum of the Galactic center, and obtain estimates of the
thermodynamic parameters of the electron plasma generating the
superluminal radiation. The cutoff energy of the high-energy cascade
fitting the TeV spectrum can be related to anisotropies in the cosmic
ray spectrum detected by the AGASA and SUGAR air shower arrays [11] and [12]. If the TeV
cascade is generated by a protonic source population, this requires a
thermal proton density at ![]() .
This cutoff temperature very closely matches the upper energy edge of
both the AGASA and SUGAR excess counts from the Galactic center region,
suggesting that the compact radio source Sagittarius A* is capable of
accelerating protons into the 1018 eV
region. In Section 5, we present
our conclusions.
.
This cutoff temperature very closely matches the upper energy edge of
both the AGASA and SUGAR excess counts from the Galactic center region,
suggesting that the compact radio source Sagittarius A* is capable of
accelerating protons into the 1018 eV
region. In Section 5, we present
our conclusions.
2. Thermodynamic variables of Fermi power-law ensembles
We start with the fermionic partition function,
and H=mγ is the free Hamiltonian. The electronic Lorentz factors γ=(1−υ2)−1/2 range in an interval γ1
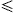 γ<∞.
H1=mγ1
is the lower threshold energy, and γ1≥1
the lower edge of Lorentz factors of the electron distribution. The
momentum parametrization is
γ<∞.
H1=mγ1
is the lower threshold energy, and γ1≥1
the lower edge of Lorentz factors of the electron distribution. The
momentum parametrization is The grand partition function (2.1) is
obtained via a standard trace calculation in fermionic occupation
number representation,
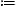 H1.
We briefly sketch the derivation of partition function (2.1) from the
trace (2.3). A basis |n
H1.
We briefly sketch the derivation of partition function (2.1) from the
trace (2.3). A basis |n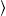 for the occupation number representation of the fermionic
creation/annihilation operators
for the occupation number representation of the fermionic
creation/annihilation operators We employ box quantization, discretizing the wave vector as ![]() .
The following summations are taken over integer lattice points
.
The following summations are taken over integer lattice points ![]() in R3,
corresponding to periodic boundary conditions on a box of size L3.
By making use of
in R3,
corresponding to periodic boundary conditions on a box of size L3.
By making use of ![]() ,
we may write trace (2.3) over the
basis states |n
,
we may write trace (2.3) over the
basis states |n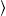 as
as
The continuum limit L→∞ amounts to replacing the summation over the lattice wave vectors by the integration
The internal energy,
are obtained from the integral representation (2.1),
Here we have reparametrized the momentum integration
where the logarithm in the integrand of (2.8) has been removed by a partial integration. That is, we write the integrand in (2.8) as f(γ)g′(γ)/3, with
For the remainder of this section, we derive the
quasiclassical fugacity expansions of the thermodynamic variables. In
Section 3, we will
discuss the low- and high-temperature limits of these expansions and
conditions for their applicability. We start by expanding partition
function (2.8) in
ascending powers of ![]() ,
,
so that K1=K and Kn=Kn,0. Differentiation with respect to β is denoted by a prime,
We eliminate the fugacity in the partition function and the internal energy by inverting
with expansion parameter
The following expansions are ascending series in
as well as the internal energy
Ucl is the classical limit, the internal energy of a Boltzmann power-law density [4], and the first two series coefficients in (2.19) read
The fugacity expansion of the entropy function
is obtained by substituting the ascending
We find
where the coefficients u1,2 are defined in (2.20), and
is the entropy of a classical Boltzmann power-law density, cf. Ref. [4] and (4.13), with a term
The thermal equation of state is derived from the Helmholtz
free energy,
The fugacity expansion of the chemical potential μ=∂F/∂N=−mα/β is found by substituting the series expansion (2.22) of α.
The isochoric specific heat and the isothermal compressibility
are
where CV,cl denotes the classical limit
To obtain the quantum correction of the isothermal compressibility, we have to iteratively solve (2.26) for V (since
where κT,cl=1/P is the classical limit. Thermodynamic stability requires CV≥0 and κT≥0. The leading order of the fugacity expansion of CV in (2.28) and κT in (2.30) is in either case positive, as it coincides with the classical limit based on a Boltzmann power-law density [4].
3. Equations of state, entropy, and heat capacity of fermionic power-law densities in the quasiclassical regime
3.1. Low-temperature asymptotics
In the quasiclassical regime covered by the fugacity
expansions in Section 2, the
low-temperature limit of the thermodynamic variables is determined by
the β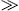 1 asymptotics of integral K(δ,β,γ1)
in (2.11). At γ1=1,
the asymptotic 1/β-series
reads
1 asymptotics of integral K(δ,β,γ1)
in (2.11). At γ1=1,
the asymptotic 1/β-series
reads
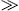 1) is given in Ref. [15].) The
series coefficients in the fugacity expansions are composed of certain K-ratios.
Using the notation (2.12), we find
1) is given in Ref. [15].) The
series coefficients in the fugacity expansions are composed of certain K-ratios.
Using the notation (2.12), we find and the same for K2,1/(K1,1K1), with 45/16 replaced by 57/16. As for coefficient u1 in (2.20), we note
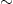 1 in leading order. Since
1 in leading order. Since where the ellipsis indicates terms of
where the quantum correction ∝N/V stems from the linear
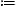 U/N−m,
so that β∝m/Eav
in leading order. We thus recover the nonrelativistic wave-mechanical
scaling
U/N−m,
so that β∝m/Eav
in leading order. We thus recover the nonrelativistic wave-mechanical
scaling The leading quantum correction to entropy, heat capacity, and
compressibility scales linearly with density N/V.
As for the entropy, cf. (2.23) and (2.24), we find
The classical isothermal compressibility is κT,cl=1/P, and the quantum correction is found as, cf. (2.30),
The series expansions (3.3)–(3.7) are in ascending powers of N/V or P. We have only stated the leading quantum correction, that is, the term linear in N/V or P. The indicated temperature scaling of this term is meant in leading order as well, the next-to-leading order being smaller by a factor of O(1/β), cf. (3.3).
3.2. Fugacity expansion and thermal wavelength in the high-temperature limit
Like in Section 3.1, the
quasiclassical high-temperature asymptotics of the thermodynamic
variables are based on the ascending ![]() -series
-series
![]() derived in Section 2, namely U
in (2.19), S
in (2.23), the
thermal equation of state (2.26), and CV
in (2.28). As for
the compressibility κT,
we will use the ascending P-series
in (2.30). The
leading quantum correction to these variables is the term linear in
derived in Section 2, namely U
in (2.19), S
in (2.23), the
thermal equation of state (2.26), and CV
in (2.28). As for
the compressibility κT,
we will use the ascending P-series
in (2.30). The
leading quantum correction to these variables is the term linear in ![]() or P,
which is in all cases composed of the K-ratios,
cf. (2.11) and (2.12),
or P,
which is in all cases composed of the K-ratios,
cf. (2.11) and (2.12),
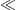 1)
of these ratios is calculated from the ascending β-series
of integral K(δ,β,1)
in (2.11), cf.
Ref. [15]. The
structure of the high-temperature expansion of K(δ,β,1)
depends on the power-law index δ.
In the following, we list the thermodynamic functions at integer
power-law indices δ=0,1,…,4.
These indices exhaust all qualitatively different cases; non-integer
power-law indices can be dealt with in the same way, based on the β-expansions
of K(δ,β,γ1)
in Ref. [15], which
cover real δ
as well as ultra-relativistic threshold Lorentz factors γ1
1)
of these ratios is calculated from the ascending β-series
of integral K(δ,β,1)
in (2.11), cf.
Ref. [15]. The
structure of the high-temperature expansion of K(δ,β,1)
depends on the power-law index δ.
In the following, we list the thermodynamic functions at integer
power-law indices δ=0,1,…,4.
These indices exhaust all qualitatively different cases; non-integer
power-law indices can be dealt with in the same way, based on the β-expansions
of K(δ,β,γ1)
in Ref. [15], which
cover real δ
as well as ultra-relativistic threshold Lorentz factors γ1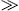 1. In this subsection, we study γ1=1
and integer power-law indices 0
1. In this subsection, we study γ1=1
and integer power-law indices 0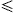 δ
δ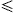 4.
4.
At δ=0,
a thermal Fermi–Dirac distribution is recovered, admitting the
quasiclassical high-temperature expansions [14]
There is no qualitative difference to the Fermi–Dirac variables (3.9) as yet. The entropy has the usual logarithmic divergence, the heat capacity approaches a finite limit, and the internal energy has a 1/β divergence. All quantum corrections vanish for β→0. At δ=2, we obtain
In the thermal equation of state and the compressibility, the quantum correction is augmented by a factor of 1/β as compared to the previous cases δ=0,1, which has implications for the thermal wavelength, cf. after (3.16). The quantum correction to the compressibility is of the same order as in the thermal equation, since P
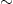 mN/(βV).
mN/(βV).
For index δ=3,
there emerges a logarithmic temperature dependence already in the
classical internal energy and heat capacity [4]. Introducing
the shortcut
The entropy diverges very slowly for β→0, owing to a double-logarithmic divergence. The heat capacity approaches zero logarithmically, but stays positive at finite temperature. The quantum corrections vanish logarithmically, except for κT. At δ=4, the expansions read
with lE(β) defined in (3.12). In this case, the internal energy diverges logarithmically, and the entropy approaches a finite limit at β=0. (For power-law indices δ>4, the internal energy reaches saturation, attaining a finite limit at β=0 like the entropy, since integral (2.6) stays finite without exponential cutoff.) In (3.14), the quantum correction to the thermal equation is in leading order independent of β, approaching the indicated finite limit linear in N/V. The quantum correction to the specific heat has the same linear β-dependence as the classical term, in leading order that is, and both terms are positive. (At δ=5, the classical term as well as the quantum correction scale ∝β2lE(β) in leading order, with positive proportionality constants.)
In the fugacity expansions (3.9), (3.10), (3.11), (3.12), (3.13) and (3.14), the quantum correction is the term linear in N/V (or P in the case of κTP). Only the leading order in β is indicated, in the classical term as well as the quantum correction, except for the entropy function in (3.14), where the next-to-leading order in β is included in the quantum correction, so that the heat capacity can be recovered by differentiation, cf. (2.27). Otherwise, the omitted β-terms are by at least a factor of O(βlogβ) smaller than the indicated ones. (In the expansion procedure, the logs are treated as constants.) The ellipses in expansions (3.9), (3.10), (3.11), (3.12), (3.13) and (3.14) indicate higher-order quantum corrections in powers of N/V. The units are restored by replacing m by mc2 on the left-hand side of the above equations as well as in β, cf. after (2.2); on the right-hand side, m is replaced by mc/ħ.
As mentioned after (3.8),
high-temperature expansions at a non-integer power-law exponent δ
are calculated analogously, by making use of ratios (3.8) and the
expansions of K(δ,β,1)
in Ref. [15].
High-temperature expansions of thermodynamic variables are differently
structured in different δ-intervals,
n−1<δ<n,
joining the expansions (3.9), (3.10), (3.11), (3.12), (3.13) and (3.14) at
integer δ.
Ultra-relativistic high-temperature expansions of K(δ,β,γ1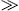 1) have been obtained in Ref. [15] as well, to
be substituted into the ratios (3.8) in the
case of power-law distributions with Lorentz factors exceeding a
high-energy threshold, cf. (2.3).
1) have been obtained in Ref. [15] as well, to
be substituted into the ratios (3.8) in the
case of power-law distributions with Lorentz factors exceeding a
high-energy threshold, cf. (2.3).
Returning to the thermal equation of state (2.26), we
define the thermal wavelength λT
by writing the leading quantum correction in (2.26) as
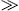 1. The numerical proportionality
factors in
1. The numerical proportionality
factors in where lE(β) denotes the logarithmic temperature dependence (3.12). If δ
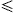 3,
we invert the caloric equation of state to find in leading order, cf. (3.9), (3.10), (3.11), (3.12) and (3.13),
3,
we invert the caloric equation of state to find in leading order, cf. (3.9), (3.10), (3.11), (3.12) and (3.13), where Eav stands for the mean particle energy U/N, and β
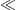 1
is implied. On combining (3.16) and (3.17), we find
the high-temperature dispersion relation λT(Eav).
At δ=0,1,
we recover the ultra-relativistic wave-mechanical scaling λT∝1/Eav.
For δ≥4,
the thermal wavelength is proportional to the Compton wavelength, λT∝1/m.
For intermediate power-law indices, the thermal wavelength is a hybrid
of ultra-relativistic and Compton wavelength, e.g.,
1
is implied. On combining (3.16) and (3.17), we find
the high-temperature dispersion relation λT(Eav).
At δ=0,1,
we recover the ultra-relativistic wave-mechanical scaling λT∝1/Eav.
For δ≥4,
the thermal wavelength is proportional to the Compton wavelength, λT∝1/m.
For intermediate power-law indices, the thermal wavelength is a hybrid
of ultra-relativistic and Compton wavelength, e.g., 4. Superluminal γ-rays from the Galactic center: Tachyonic spectral maps and electronic source distributions
In this section, we average tachyonic radiation densities [15] with fermionic power-law distributions, and use the spectral averages to perform a cascade fit to the γ-ray broadband of the Galactic central source Sagittarius A*, cf. Fig. 1 and Fig. 2. The thermodynamic parameters of the electron plasma in the Galactic center generating the superluminal cascades are extracted from the spectral fit, cf. Table 1. First we briefly summarize the tachyonic radiation densities, cf. (4.1) and (4.2), then we explain the spectral averaging, in particular the fugacity expansion of the spectral functions and their low- and high-temperature asymptotics, cf. (4.3), (4.4), (4.5), (4.6), (4.7), (4.8), (4.9), (4.10), (4.11), (4.12), (4.13), (4.14), (4.15), (4.16), (4.17), (4.18) and (4.19). The spectral fit in Fig. 1 and Fig. 2 is discussed after (4.20).
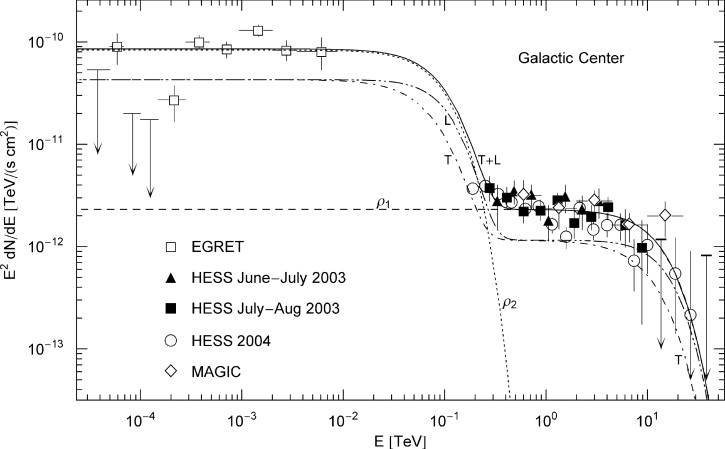
Fig. 1. γ-ray
wideband of the Galactic center. EGRET data points from Ref. [2], HESS points
from Refs. [7] and [8], MAGIC
points from Ref. [9]. EGRET
points refer to the source 3EG J1746 − 2851, HESS and
MAGIC points to HESS J1745 − 290. The solid line T+L
depicts the unpolarized differential tachyon flux ![]() ,
obtained by adding the flux densities ρ1,2
of two electron populations and rescaled with E2
for better visibility of the spectral curvature, cf. (4.20). The
transversal (T, dot-dashed) and longitudinal (L, double-dot-dashed)
flux densities
,
obtained by adding the flux densities ρ1,2
of two electron populations and rescaled with E2
for better visibility of the spectral curvature, cf. (4.20). The
transversal (T, dot-dashed) and longitudinal (L, double-dot-dashed)
flux densities ![]() add up to the total flux T+L. The χ2-fit
is done with the unpolarized tachyon flux T+L, and subsequently split
into transversal and longitudinal components. The exponential decay of
the cascades ρ1,2
sets in at about
add up to the total flux T+L. The χ2-fit
is done with the unpolarized tachyon flux T+L, and subsequently split
into transversal and longitudinal components. The exponential decay of
the cascades ρ1,2
sets in at about ![]() ,
implying cutoffs at 5.5 TeV for the ρ1
cascade and at 38 GeV for ρ2,
which terminate the spectral plateaus. The unpolarized flux T+L is the
actual spectral fit, the parameters of the electron densities are
recorded in Table 1.
,
implying cutoffs at 5.5 TeV for the ρ1
cascade and at 38 GeV for ρ2,
which terminate the spectral plateaus. The unpolarized flux T+L is the
actual spectral fit, the parameters of the electron densities are
recorded in Table 1.
Electronic source densities ρ1,2 generating the γ-ray broadband of the TeV source HESS J1745 − 290 and the associated EGRET source 3EG J1746 − 2851 in the Galactic center region
Each ρi
stands for a Maxwell–Boltzmann density ![]() ,
cf. (4.13). β
is the cutoff parameter in the Boltzmann factor.
,
cf. (4.13). β
is the cutoff parameter in the Boltzmann factor. ![]() determines the amplitude of the tachyon flux generated by ρi,
from which the electron count
determines the amplitude of the tachyon flux generated by ρi,
from which the electron count ![]() is inferred at the indicated distance of 8 kpc, cf. after (4.21). (The
subscript 1 in
is inferred at the indicated distance of 8 kpc, cf. after (4.21). (The
subscript 1 in ![]() and
and ![]() has been dropped.)
has been dropped.) ![]() is the electron temperature, and U
(erg) the internal energy of the thermal densities ρi.
The cascades labeled ρ1,2
in Fig. 1
and Fig. 2
are obtained by averaging the tachyonic radiation densities (4.1) with the
electron densities ρi,
cf. (4.14), (4.15) and (4.16). The
parameters β
and
is the electron temperature, and U
(erg) the internal energy of the thermal densities ρi.
The cascades labeled ρ1,2
in Fig. 1
and Fig. 2
are obtained by averaging the tachyonic radiation densities (4.1) with the
electron densities ρi,
cf. (4.14), (4.15) and (4.16). The
parameters β
and ![]() are extracted from the least-squares fit T+L in Fig. 1.
are extracted from the least-squares fit T+L in Fig. 1.
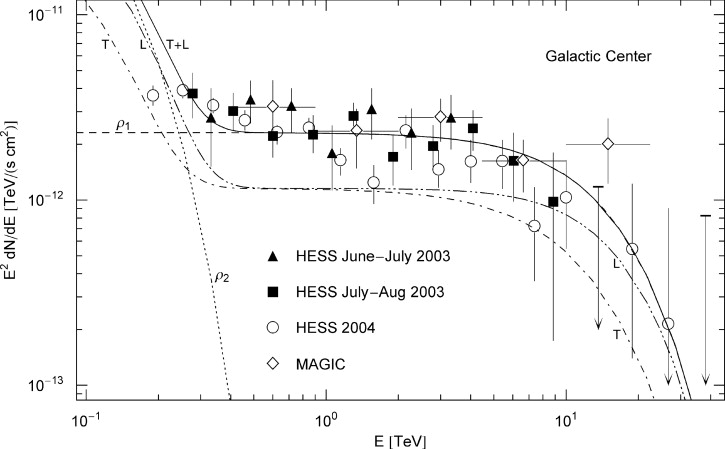
Fig. 2. Close-up of the HESS spectrum in Fig. 1. The TeV spectral map coincides with the ρ1 cascade, since the ρ2 flux is exponentially cut at 38 GeV. T and L stand for the transversal and longitudinal flux components, and T+L labels the unpolarized flux. The HESS points define a spectral plateau in the high GeV range typical for tachyonic cascade spectra [15] and [16]. The spectral curvature is intrinsic, being generated by the Boltzmann factor in the electron densities.
The quantized tachyonic radiation densities of a uniformly
moving spinning charge read [16]
Only frequencies in the range 0
 ω
ω ωmax(γ)
can be radiated by a uniformly moving charge, the tachyonic spectral
densities
ωmax(γ)
can be radiated by a uniformly moving charge, the tachyonic spectral
densities 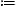 mt/(2mμt).
The tachyon–electron mass ratio gives υmin/c≈2.1×10−3,
cf. Ref. [18].
mt/(2mμt).
The tachyon–electron mass ratio gives υmin/c≈2.1×10−3,
cf. Ref. [18].
The radiation densities (4.1) refer to a
single charge with Lorentz factor γ.
We average them with a Fermi power-law distribution,
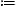 m3V/π2,
cf. (2.6), (2.7) and (2.8). The
particle number is
m3V/π2,
cf. (2.6), (2.7) and (2.8). The
particle number is The spectral average of the radiation densities (4.1) is carried
out as
The average (4.4) can be reduced to the fermionic spectral functions
with lower integration boundary γ1≥μt, cf. after (4.2). The threshold Lorentz factor γ1 defines the break frequency [19]
which separates the spectrum into a low- and high-frequency band. In particular,
with
where the coefficients fk read
with density
The quasiclassical fugacity expansion of the spectral
functions (4.9) is found
by expanding density (4.3) in
ascending powers of ![]() ,
cf. (2.10),
,
cf. (2.10),
The classical limit of the fermionic density
with normalization
The classical limit of the fermionic spectral functions ![]() in (4.6) is the
Boltzmann average [15]
in (4.6) is the
Boltzmann average [15]
which can also be obtained from the Fermi functions
where
In the low-temperature limit, βγ1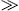 1, the incomplete
1, the incomplete ![]() -functions
occurring in the fugacity expansion of fk(γ1)
in (4.12) can be
replaced by the asymptotic series
-functions
occurring in the fugacity expansion of fk(γ1)
in (4.12) can be
replaced by the asymptotic series
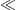 1.
In the fugacity expansion (4.12) of the
reduced spectral functions, we can therefore substitute the ascending
series
1.
In the fugacity expansion (4.12) of the
reduced spectral functions, we can therefore substitute the ascending
series If k−δn is zero or a negative integer, k−δn=−m, m≥0, we use instead of (4.18) the ascending series of the exponential integral Em+1(βγ1),
The spectral fit in Fig. 1 and Fig. 2 is based on the E2-rescaled flux densities [20]
where d is the distance to the source and
which is independent of the distance estimate in (4.20). Here,
Fig. 1 and Fig. 2 show the spectral map of the TeV γ-ray source HESS J1745 − 290 and the GeV source 3EG J1746 − 2851. Both sources are located in the vicinity of the unidentified compact radio source Sagittarius (Sgr) A* at the core of the Galactic center region, which comprises the supernova remnant Sgr A East and the pulsar wind nebula G359.95 − 0.04, as well as molecular cloud complexes such as Sgr B and Sgr C [21] and [22].
In Table 1,
we list the thermodynamic parameters of the electron populations
generating the tachyonic cascade spectra ρ1,2
depicted in the figures. In the case of protonic source densities (4.13), the
cutoff energy ![]() in the Boltzmann factor has to be multiplied by 1.84×103,
the proton/electron mass ratio, resulting in a cutoff energy of 1016.2 eV
for a protonic ρ2
population. The protonic high-energy population ρ1
is cut at 1018.4 eV, which is to be
compared to the excess fluxes from the Galactic center region observed
by AGASA in the 1018–1018.4 eV
range [11], and the
SUGAR array in the 1017.9–1018.5 eV
interval [12].
in the Boltzmann factor has to be multiplied by 1.84×103,
the proton/electron mass ratio, resulting in a cutoff energy of 1016.2 eV
for a protonic ρ2
population. The protonic high-energy population ρ1
is cut at 1018.4 eV, which is to be
compared to the excess fluxes from the Galactic center region observed
by AGASA in the 1018–1018.4 eV
range [11], and the
SUGAR array in the 1017.9–1018.5 eV
interval [12].
The tachyonic spectral maps are further explained in the
figure captions, and can be compared to electromagnetic inverse-Compton
fits [23] or hadronic
fits based on proton–proton scattering and pion decay [2] and [24]. The
electronic source count for the Crab Nebula at ![]() is 1.9×1050, cf. Ref. [16], as
compared to 3.4×1049 for HESS
J1745 − 290 and 3EG J1746 − 2851,
at a distance of 8 kpc, cf. Table 1.
The internal energy of the electron gas is 7.2×1051 erg,
to be compared to hadronic model estimates predicting 5×1045 erg [24], 1049–1050 erg [25], and 5.1×1050 erg [23] for a
protonic source population.
is 1.9×1050, cf. Ref. [16], as
compared to 3.4×1049 for HESS
J1745 − 290 and 3EG J1746 − 2851,
at a distance of 8 kpc, cf. Table 1.
The internal energy of the electron gas is 7.2×1051 erg,
to be compared to hadronic model estimates predicting 5×1045 erg [24], 1049–1050 erg [25], and 5.1×1050 erg [23] for a
protonic source population.
5. Conclusion
We have investigated superluminal radiation from electron populations in the Galactic center region, and found the thermodynamic parameters of the source densities. We demonstrated that the γ-ray wideband of the Galactic center can be fitted with a tachyonic cascade spectrum. In particular, the extended spectral plateau in the MeV–GeV range as well as the spectral curvature apparent in double-logarithmic plots are reproduced by the cascade fit in Fig. 1 and Fig. 2. Estimates of the temperature, the source count, and the internal energy of the electron plasma generating the superluminal cascades are given in Table 1.
In Section 4, we averaged the superluminal radiation densities with fermionic power-law distributions, and derived the quantized spectral functions. The power-law densities in Sections Sections 2 and 3 and the spectral averages were studied mostly in the quasiclassical limit, as γ-ray spectral fits are done in the high-temperature regime. The opposite asymptotic limit of nearly degenerate fermionic power-law ensembles at low temperature and high density will be discussed elsewhere.
We quantized Boltzmann power-law densities in Fermi–Dirac statistics, derived the fermionic partition function, developed the Legendre formalism of fermionic power-law distributions, and calculated the fugacity expansion of the thermodynamic variables, cf. Section 2. The qualitative dependence of the variables on the electronic power-law index, the temperature scaling of the quantum corrections, and the thermal wavelength of power-law ensembles were investigated in Section 3. We have focused on γ-ray spectra, which can be fitted with ultra-relativistic electron densities at high temperature, cf. Section 4. As for tachyonic X-ray spectra obtained from diffraction gratings [21], the tachyon mass of 2 keV has to be included in the dispersion relation when parametrizing the glancing angle in the Bragg condition with energy, which affects the shape of the spectral maps in the X-ray bands; this will be discussed elsewhere. The spectral fit in Fig. 1 and Fig. 2 is performed with the unpolarized tachyon flux. At γ-ray energies, the speed of tachyons is close to the speed of light, the basic difference to electromagnetic radiation being the longitudinal flux component [26]. The polarization of tachyons can be determined from transversal and longitudinal ionization cross-sections of Rydberg atoms, which peak at different scattering angles [27].
Acknowledgements
The author acknowledges the support of the Japan Society for the Promotion of Science. The hospitality and stimulating atmosphere of the Centre for Nonlinear Dynamics, Bharathidasan University, Trichy, and the Institute of Mathematical Sciences, Chennai, are likewise gratefully acknowledged.