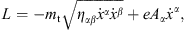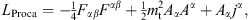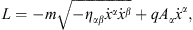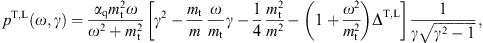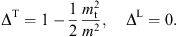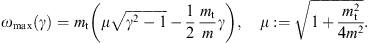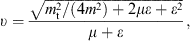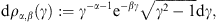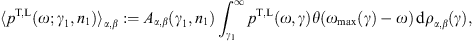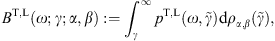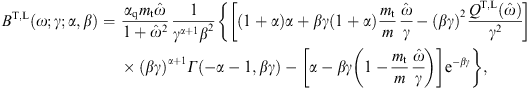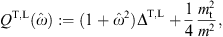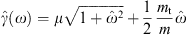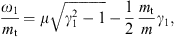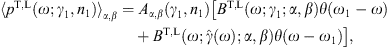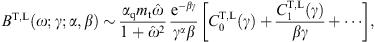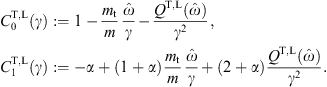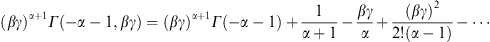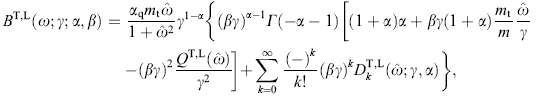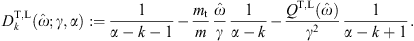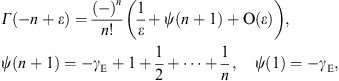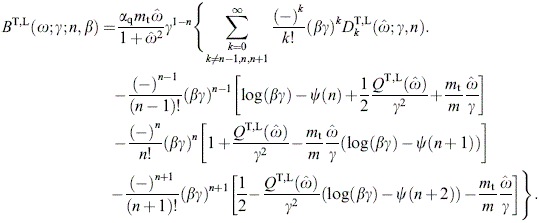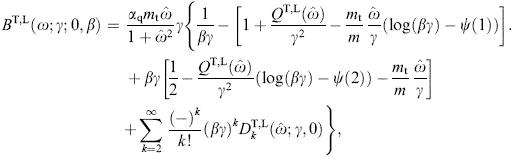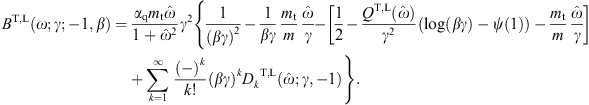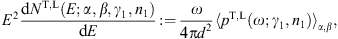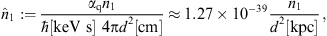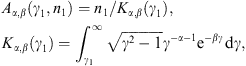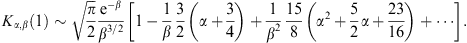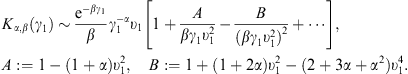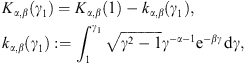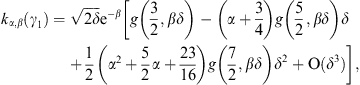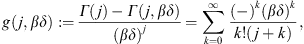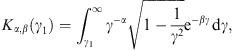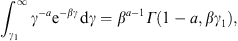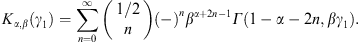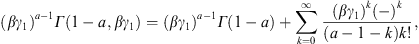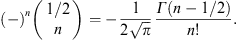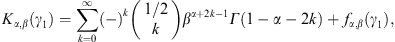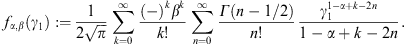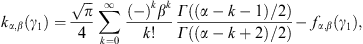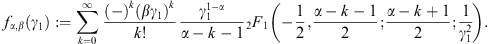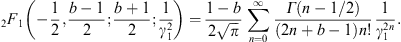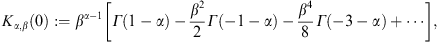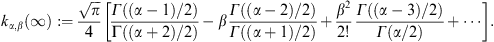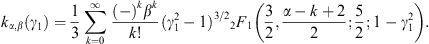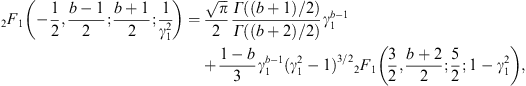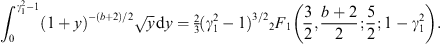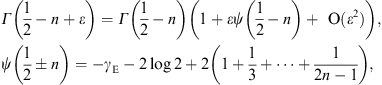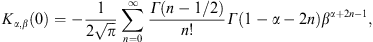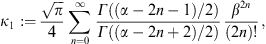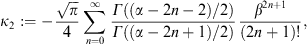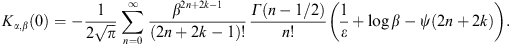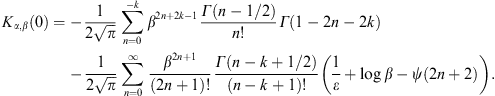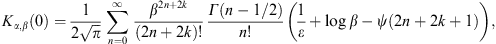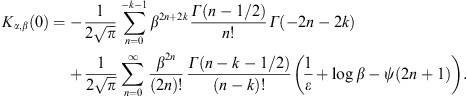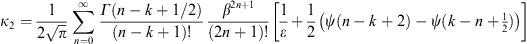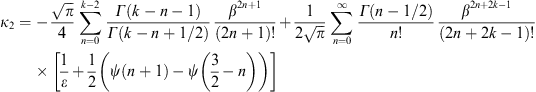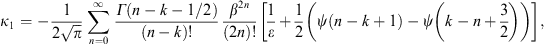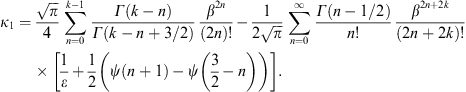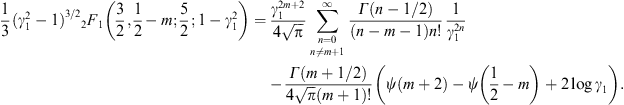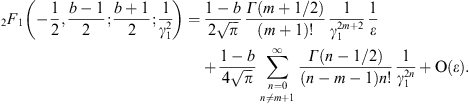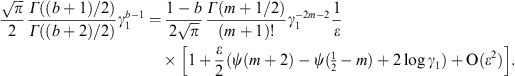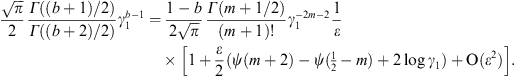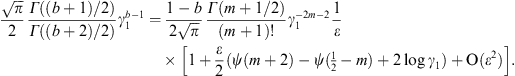Volume 322, Issue 3, March 2007, Pages 677-700
Roman
Tomaschitz ,
a,
,
a,

Abstract
Astrophysical radiation sources are scrutinized in search of superluminal γ-rays. The tachyonic spectral densities generated by ultra-relativistic electrons in uniform motion are fitted to the high-energy spectra of Galactic supernova remnants, such as RX J0852.0−4622 and the pulsar wind nebulae in G0.9+0.1 and MSH 15-52. The superluminal spectral maps of the unidentified TeV γ-ray sources HESS J1303−631, TeV J2032+4130 and HESS J1825−137 are inferred from EGRET, HEGRA and HESS data. Tachyonic cascade spectra are quite capable of generating the spectral curvature seen in double-logarithmic plots, as well as the extended spectral plateaus defined by EGRET flux points in the GeV band. The curvature of the TeV spectra is intrinsic, caused by the Boltzmann factor in the source densities. The spectral averaging with thermal and exponentially cut power-law electron densities can be done in closed form, and systematic high- and low-temperature expansions of the superluminal spectral densities are derived. Estimates on the electron/proton populations generating the tachyon flux are obtained from the spectral fits, such as power-law indices, temperature and source counts. The cutoff temperatures of the source densities suggest ultra-high-energy protons in MSH 15-52, HESS J1825−137 and TeV J2032+4130.
Keywords: Superluminal radiation; Tachyonic γ-rays; Cosmic rays; Spectral averaging; Spectral curvature
PACS classification codes: 03.50.Kk; 05.30.Ch; 11.10.Lm; 95.30.Gv
Article Outline
- 1. Introduction
- 2. Tachyonic spectral densities of freely moving electrons
- 3. Tachyonic spectral averages and spectral fits
- 4. Conclusion
- Acknowledgements
- Appendix A. Asymptotic normalization of the electronic source densities
- Appendix B. ε-expansion of the normalization factors Kα,β(γ1) at integer electron index α
- References
1. Introduction
The traditional way to introduce faster-than-light particles
(tachyons) is to start with the Lagrangian
respectively, where mt is the mass of the Proca field Aα. The mass term in (1.3) is added with a positive sign, so that
At first sight, the formalism closely resembles electrodynamics, but there are differences as well. Apart from the superluminal speed of the quanta, the radiation is partially longitudinally polarized [7]. A basic feature of photons traveling over cosmological distances is their ability to propagate dispersion free, as the wave fields are conformally coupled to the background metric. This property is also retained for tachyons, as the tachyon mass scales inversely with the cosmic expansion factor [5]. There is no interaction of tachyons with photons, they couple only indirectly via matter fields. Therefore, contrary to electromagnetic γ-rays, high-energy tachyons cannot interact with the infrared background radiation, so that there is no attenuation of the extragalactic tachyon flux due to electron–positron pair creation.
The most pronounced difference between electromagnetic and tachyonic radiation lies in the emission process itself. Freely moving electrons can radiate superluminal quanta. Radiation densities attached to a uniformly moving charge have no analog in electrodynamics, their very existence has substantial implications for the space–time structure, requiring an absorber that breaks the time symmetry of the emission process [8]. The tachyonic radiation densities depend on the velocity of the uniformly moving charge in the rest frame of the cosmic absorber, and there is a radiation threshold, a minimal speed for superluminal radiation to occur [9]. The Green function of this radiation process is time-symmetric, there is no retarded propagator supported outside the lightcone. The advanced modes of the radiation field are converted into retarded ones by virtue of a nonlocal, instantaneous interaction with the cosmic absorber medium [10]. The latter also defines a universal frame of reference necessary to render the superluminal signal transfer causal. The time symmetry of the Green function implies that there is no radiation damping, the radiating charge stays in uniform motion. The energy radiated is supplied by the oscillators constituting the absorber medium.
The quantization of superluminal field theories has constantly been marred by the fact that there is no relativistically invariant way to distinct positive and negative frequency solutions outside the lightcone, a consequence of time inversions by Lorentz boosts. When attempting quantization, the result was either unitarity violation or a non-invariant vacuum state [2] and [4]. Therefore, relativistic interactions of superluminal quanta with matter have never been worked out to an extend that they could be subjected to test. In fact, tachyons have not been detected so far, and one may ask why. There is the possibility that superluminal signals just do not exist, the vacuum speed of light being the definitive upper bound. In an open universe, however, this is not a particularly appealing perspective. There is another explanation, the interaction of superluminal radiation with matter is very weak, the quotient of tachyonic and electric fine structure constants being αq/αe ≈ 1.4 × 10−11, and therefore superluminal quanta are just hard to detect [5]. There have been searches for superluminal particles, which were assumed to be electrically charged sources of vacuum Cherenkov radiation, and bubble-chamber events were reanalyzed in search of negative mass-squares inferred from energy–momentum conservation [11]. Apart from that, tachyonic quanta should have been detected over the years, accidentally, despite of their tiny interaction with matter. The most likely reason as to why this has not happened is this: Due to our contemporary spacetime conception, we are obliged to systematically ignore them.
In fact, in a relativistic spacetime view, superluminal signals are causality violating, irrespectively of the special mechanism of the transmission. If two events are connected by a tachyonic signal, a Lorentz boost can interchange the time order, so that some observers will see the effect preceding the cause, absorption preceding emission, for instance [4]. Hence, outside the lightcone, in the domain of tachyonic signal transfer, there is no relativistically invariant meaning to cause and effect. Clearly, there are acausal solutions in electrodynamics as well, advanced wave fields, and even in Newtonian mechanics one can easily specify acausal initial conditions such as a negative time delay. However, these solutions can be identified and discarded on the grounds of causality violation. When superluminal signals are involved in a relativistic context, this cannot be done, as there is no invariant way to distinct causal from acausal solutions. What appears causal to one observer is acausal to others, since Lorentz boosts can invert the time order of spacelike connections. This is in strong contrast to the retarded wave fields of electrodynamics, which stay retarded in all frames. Retarded superluminal waves, however, will usually acquire an advanced acausal component if subjected to Lorentz boosts. Superluminal signals are thus incompatible with the relativity principle, as they unavoidably entail causality violation, quite independently of the physical mechanism of the signal transfer [5]. This suggests to use an absolute spacetime conception when dealing with tachyons. Relativity theory is a theory of subluminal motion, and the extension of the relativity principle to spacelike connections conflicts with causality. To reconcile superluminal signals with the causality principle, it is necessary to find an absolute time order as defined by cosmic time in the comoving galaxy frame, the rest frame of the absorber medium. The cosmic time order unambiguously determines the causality of events connected by superluminal signals. All observers can arrive at the same conclusion by synchronizing their proper time with cosmic time, irrespectively of time inversions that may occur in individual rest frames [10]. Had there been detection in the above mentioned searches, in the relativistic framework in which they were interpreted, this would have been tantamount to causality violation. By contrast, the radiation mechanism suggested here, based on a Proca field with negative mass-square minimally coupled to subluminal matter, is non-relativistic, as it invokes the absolute spacetime defined by the absorber, even though the Lagrangians are covariant.
Unitarity violation [12], an unstable vacuum [4] and causality violation [13] are inextricably linked with relativistic superluminal field theories. Unitarity violation means that the quantum mechanical probability amplitude is not conserved, an incurable inconsistency. The term ‘unstable vacuum’ is a misnomer suggesting that there are field theories with a stable vacuum and others with an unstable one, just like stable and unstable dynamical systems. An unstable vacuum, however, has nothing to do with dynamical instability. It is an inconsistency arising in quantization attempts of relativistic superluminal theories and implies an energy functional unbounded from below, so that one ends up with a finite system from which an infinite amount of energy can be extracted, a perpetuum mobile. Indefinite energy functionals can be traced back to causality violation endemic in relativistic theories of superluminal signal transfer. Attempts to cure the problem of negative energies in terms of an antiparticle reinterpretation analogous to the Dirac Hamiltonian have failed, as causality remains violated [4]; the indefinite classical energy functional of the Dirac theory is not related to causality violation, after all.
The technical reason why it is not possible to consistently define a positive definite energy functional in a relativistic superluminal field theory is elementary and does not depend on the specific modeling of the signal transfer. Lorentz boosts can change the sign of the energy component of a spacelike 4-momentum, so that negative frequency modes are generated, which can be made arbitrarily large by choosing a suitable boost. This is also the root of causality violation; Lorentz boosts can change the time order of spacelike connections, so that one can always find inertial frames in which the effect precedes the cause.
It has been argued that causality-violating signal transfer outside the lightcone is not a logical inconsistency [13], implying that the only way to figure out whether tachyons comply with the causality principle is to find them and to settle this empirically. This is presumably true, but the trouble here is that relativistic acausal theories have been very inefficient with regard to suggestions where to look for tachyons. Causality may not be a logical necessity, but it is a practical one regarding physical modeling. Without supposition of the causality principle (that is, every effect has a cause, the cause precedes the effect, and the terms cause and effect can be invariantly attached to the respective events) one will most likely spend one’s time solving causality paradoxa [14] rather than calculating cross sections, the latter being indispensable for quantitative suggestions as to where to find tachyons.
A consistent quantization, implying causality, a stable vacuum and a unitary scattering matrix, can be achieved if we refrain from modeling superluminal signals on the basis of a local relativistic spacetime and invoke an absolute time order instead when dealing with spacelike momenta. The criterion for the usefulness of any given spacetime conception, the use of an expanding 3-space in cosmology to model redshifts for instance, is efficiency regarding physical modeling in a given context. A spacetime concept has no physical reality by itself and has to be adapted to the context, not the other way round. We employ an absolute spacetime for the modeling of superluminal signal transfer, since an extension of the relativistic spacetime concept to spacelike momenta is counterproductive in dealing with superluminal signals.
A relativistic spacetime conception has at its core the Galilean assertion of the equivalence of uniform motion and rest. The laws of physics are the same in all inertial frames, the latter are considered equivalent and synchronized by a group of coordinate transformations such as Lorentz boosts. In particular, there is no distinguished state of rest, the substitute for this is uniform inertial motion. One can even single out a preferred frame, such as the comoving galaxy frame defining cosmic time, this is still a relativistic concept.
An absolute space is defined by a microscopic space structure replacing the purely geometric Euclidean space concept of coordinate axes labeling the void. We assume that this space structure is a Wheeler–Feynman absorber medium [8] capable of turning advanced superluminal wave modes into retarded ones. The absorber defines the frame of absolute rest coinciding with the comoving galaxy frame, so that cosmic time provides the universal time order required in the causality principle. The absolute spacetime concept is centered at the state of rest, accelerated and inertial frames are based on this reference frame. The superluminal spectral densities studied in Section 2 are determined by the velocity of the radiating charge. This is not a relative velocity, it stands for the absolute motion of the charge in the absorber medium.
The absorber medium reminds us of the prerelativistic ether outlawed by relativity theory [15]; Michelson–Morley cannot be invoked if the absorber medium does not affect electromagnetic wave propagation. When contemplating a microscopic space structure, one has to keep in mind that it has to compete with Euclidean space, already a cubic lattice structure makes physical modeling much harder. The question thus arises how to define this space structure without compromising the efficiency of Euclidean modeling. The way to proceed is suggested by the Mach principle and the Wheeler–Feynman absorber theory.
The Mach principle tries to explain the inertial force in Newton’s equations by a nonlocal interaction with the mass content of the universe. In practice, it is not really necessary to know the details of this interaction, as the inertial force defines itself locally by mass and acceleration. The Wheeler–Feynman absorber theory was designed in the context of a time symmetric formulation of electrodynamics [8]. In this theory, the absorber comprises the collection of electric charges in the universe, its interaction with time symmetric electromagnetic fields is instantaneous and nonlocal and turns advanced wave modes into retarded ones. Here again, it is not necessary to quantify the details of this interaction such as the actual charge distribution, as the time symmetric Green function and the retarded and advanced wave fields generated are determined by the local Hamiltonian. A similar absorber concept is used for tachyonic wave propagation. Outside the lightcone, there are no retarded or advanced Green functions, the time symmetry of the wave propagation is broken by the absorber medium. One can give an explicit model of the absorber medium, in terms of uniformly distributed microscopic oscillators interacting with the time symmetric wave field [16], but this is not really necessary, as the time symmetric Green function can be calculated from the local Hamiltonian [10].
It is the interaction mechanism with matter rather than the space and causality conception that provides the clues where to search for tachyons. We work out specific examples, scrutinizing astrophysical radiation sources for superluminal γ-rays. We perform tachyonic spectral fits to the spectra of Galactic supernova remnants and other recently discovered TeV γ-ray sources. In Section 2, we explain the transversal and longitudinal spectral densities generated by uniformly moving charges as well as the spectral averaging with thermal and power-law electron distributions. These spectral densities have no analog in electrodynamics; tachyonic synchrotron densities reduce to these densities in the limit of infinite bending radius [17], but electromagnetic synchrotron radiation vanishes in this limit. In Section 3, we derive the high- and low-temperature expansions of the averaged radiation densities. Tachyonic spectral maps of the supernova remnants G0.9+0.1, RX J0852.0−4622 and MSH 15-52 as well as the unidentified TeV γ-ray sources HESS J1303−631, TeV J2032+4130 and HESS J1825−137 are obtained by fitting EGRET, HEGRA and HESS flux points. We discuss spectral peaks, breaks, slopes, and the curvature of tachyonic cascade spectra. In Section 4, we compare the cutoff temperature of the electronic/protonic source populations to the break energies in the cosmic-ray spectrum, and point out the possibility of ultra-high-energy protons in at least three of the studied TeV sources. In Appendix A, we calculate the normalization factors of the spectral densities; the singular high-temperature expansions at integer electronic power-law index are dealt with in Appendix B.
2. Tachyonic spectral densities of freely moving electrons
The quantized transversal and longitudinal radiation densities
of a uniformly moving spinning charge read [9]
Here, γ is the electronic Lorentz factor, mt/m the tachyon-electron mass ratio, and αq the tachyonic fine structure constant. A spectral cutoff occurs at
Only frequencies in the range 0 < ω < ωmax(γ) can be radiated by a uniformly moving charge, the tachyonic spectral densities pT,L(ω) are cut off at the break frequency ωmax. The radiation condition on the electronic Lorentz factor is γ > μ, cf. (2.3); since ωmax(μ) = 0, there is no emission by uniformly moving charges with Lorentz factors γ
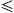 μ.
The threshold on the speed of the charge for radiation to occur is thus
υ > υmin
μ.
The threshold on the speed of the charge for radiation to occur is thus
υ > υmin 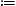 mt/(2mμ).
The units
mt/(2mμ).
The units 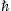 = c = 1
can easily be restored. We use the Heaviside–Lorentz system, so that αq = q2/(4π
= c = 1
can easily be restored. We use the Heaviside–Lorentz system, so that αq = q2/(4π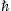 c) ≈ 1.0 × 10−13
is the tachyonic fine structure constant. The tachyon mass is mt ≈ 2.15 keV/c2.
These estimates are obtained from hydrogenic Lamb shifts [5]. The
tachyon–electron mass ratio, mt/m ≈ 1/238,
gives υmin/c ≈ 2.1 × 10−3.
c) ≈ 1.0 × 10−13
is the tachyonic fine structure constant. The tachyon mass is mt ≈ 2.15 keV/c2.
These estimates are obtained from hydrogenic Lamb shifts [5]. The
tachyon–electron mass ratio, mt/m ≈ 1/238,
gives υmin/c ≈ 2.1 × 10−3.
The spectral densities (2.1) are
generated by a Dirac current. The spectral densities of a classical
point charge are recovered by putting all mt/m-ratios
in (2.1), (2.2) and (2.3) equal to
zero, in particular, ![]() and
and ![]() ,
and the classical spectral cutoff occurs at
,
and the classical spectral cutoff occurs at ![]() .
In the ultra-relativistic limit, γ
.
In the ultra-relativistic limit, γ 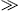 1, we can likewise drop all terms
containing mt/m-ratios,
so that the ultra-relativistic quantum densities coalesce with the
classical densities. Substantial quantum effects regarding the shape of
the spectral density emerge only in the extreme non-relativistic limit [9]. We may then
parametrize γ = μ + ε,
with ε
1, we can likewise drop all terms
containing mt/m-ratios,
so that the ultra-relativistic quantum densities coalesce with the
classical densities. Substantial quantum effects regarding the shape of
the spectral density emerge only in the extreme non-relativistic limit [9]. We may then
parametrize γ = μ + ε,
with ε  1,
so that the source velocity in the vicinity of υmin
reads
1,
so that the source velocity in the vicinity of υmin
reads
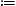 pT(ω) + pL(ω).
pT(ω) + pL(ω).
The radiation densities (2.1) refer to
single charges with Lorentz factor γ. We average
them with electron distributions, power-laws exponentially cut with
Boltzmann distributions, dρ ∝ E−2 − αe−E/(kT)d3p,
or
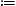 mc2/(kT).
The electronic Lorentz factors range in an interval γ1
mc2/(kT).
The electronic Lorentz factors range in an interval γ1 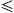 γ < ∞,
the lower edge satisfies the radiation condition γ1
γ < ∞,
the lower edge satisfies the radiation condition γ1 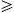 μ,
cf. after (2.3). Linear
combinations of (2.5) may be
used for wideband spectra, including pure power-laws, cf. the modeling
of γ-ray burst spectra [18] and [19] and
electron distributions in galaxy clusters [20]. The
normalization factors Aα,β(γ1,n1)
of densities (2.5) are
determined by
μ,
cf. after (2.3). Linear
combinations of (2.5) may be
used for wideband spectra, including pure power-laws, cf. the modeling
of γ-ray burst spectra [18] and [19] and
electron distributions in galaxy clusters [20]. The
normalization factors Aα,β(γ1,n1)
of densities (2.5) are
determined by The averaging is carried out via
where γ
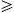 μ.
More explicitly,
μ.
More explicitly,where
with ΔT,L in (2.2).
The spectral range of the radiation densities (2.1) is
0 < ω < ωmax(γ),
cf. (2.3).
Inversely, the condition ![]() or
or
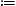 ωmax(γ1),
or
ωmax(γ1),
orwhich separates the spectrum into a low- and high-frequency band. We have
with
 pT
pT α,β
is the energy transversally radiated per unit time and unit frequency.
α,β
is the energy transversally radiated per unit time and unit frequency.
3. Tachyonic spectral averages and spectral fits
To get an overview of the averaged spectral densities (2.12), we
consider their asymptotic limits. The low-temperature expansion, β 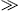 1, is readily found by substituting the
asymptotic expansion of the incomplete Γ-function [21] into the
spectral function BT,L(ω;γ;α,β),
cf. (2.8),
1, is readily found by substituting the
asymptotic expansion of the incomplete Γ-function [21] into the
spectral function BT,L(ω;γ;α,β),
cf. (2.8),
This holds for Lorentz factors γ
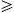 μ,
cf. after (2.5),
μ,
cf. after (2.5), 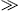 1.
1.
The high-temperature expansion, β  1,
of BT,L is obtained by
substituting the ascending series [21]
1,
of BT,L is obtained by
substituting the ascending series [21]
 1
is thus
1
is thuswith the shortcut
In the opposite limit, βγ
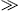 1, we may still use the low-temperature
expansion (3.1), even if β
1, we may still use the low-temperature
expansion (3.1), even if β  1.
Singularities occurring at integer α in (3.4) and (3.5) cancel if ε-expanded.
To this end, we substitute α = n − ε
as well as the ε-expansion of the Γ-function
at its poles,
1.
Singularities occurring at integer α in (3.4) and (3.5) cancel if ε-expanded.
To this end, we substitute α = n − ε
as well as the ε-expansion of the Γ-function
at its poles,valid for n
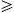 0.
At α = n
0.
At α = n 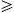 1,
we obtain
1,
we obtainAt α = 0, we find
and at α = −1,
There are no singularities in (3.4) for α
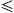 −2.
−2.
If γ1 = μ,
β  1
and α > 1, the maximum of
1
and α > 1, the maximum of 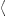 pT,L(ω; γ1, n1)
pT,L(ω; γ1, n1)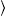 α,β,
cf. (2.12), is
determined by the leading factor
α,β,
cf. (2.12), is
determined by the leading factor ![]() in the high-temperature expansion (3.4). This peak
is located at
in the high-temperature expansion (3.4). This peak
is located at ![]() and is followed by power-law decay ∝ ω−α
for ω
and is followed by power-law decay ∝ ω−α
for ω  mt/β
and exponential decay starting at about ω ≈ mt/β.
The low-temperature expansion (3.1) applies
for ω
mt/β
and exponential decay starting at about ω ≈ mt/β.
The low-temperature expansion (3.1) applies
for ω 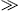 mt
/β. If γ1
mt
/β. If γ1 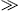 1 (but still βγ1
1 (but still βγ1  1
and α > 1), the peak of
1
and α > 1), the peak of 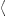 pT,L(ω; γ1, n1)
pT,L(ω; γ1, n1)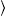 α,β
is determined by the factor
α,β
is determined by the factor ![]() in (3.4) and occurs
at ωmax ≈ mt.
It is followed by a broken power-law, at first
in (3.4) and occurs
at ωmax ≈ mt.
It is followed by a broken power-law, at first 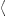 pT,L
pT,L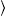 α,β ∝ 1/ω
in the range 1
α,β ∝ 1/ω
in the range 1  ω/mt
ω/mt  γ1
and then
γ1
and then 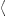 pT,L
pT,L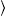 α,β ∝ ω−α
in the interval γ1
α,β ∝ ω−α
in the interval γ1  ω/mt
ω/mt  1/β.
At ω ≈ mt/β,
there is an exponential cutoff according to (3.1).
1/β.
At ω ≈ mt/β,
there is an exponential cutoff according to (3.1).
The spectral fits in Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5 and Fig. 6 are
performed with the E2-rescaled
flux density E2dNT,L/dE,
which relates to the energy density 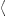 pT,L
pT,L α,β
in (2.12) as
α,β
in (2.12) as
 pT,L
pT,L α,β
give a plateau value E2dNT,L/dE ∝ 1
in the range 1
α,β
give a plateau value E2dNT,L/dE ∝ 1
in the range 1  E/(mtc2)
E/(mtc2)  γ1,
followed by power-law decay E2dNT,L/dE ∝ E1 − α
in the band γ1
γ1,
followed by power-law decay E2dNT,L/dE ∝ E1 − α
in the band γ1  E/(mtc2)
E/(mtc2)  1/β,
and subsequent exponential decay.
1/β,
and subsequent exponential decay.
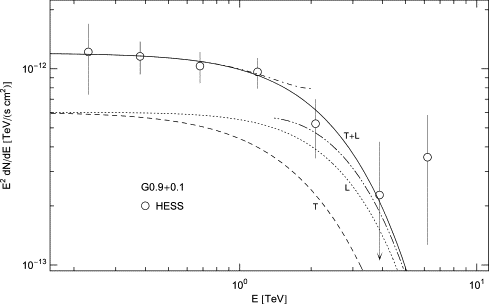
Fig. 1. Spectral map of the pulsar wind nebula in SNR G0.9+0.1. Data points from HESS [22]. The solid line T+L depicts the unpolarized differential tachyon flux dNT+L/dE, rescaled with E2 for better visibility of the spectral curvature, cf. (3.10). The transversal (T, dashed) and longitudinal (L, dotted) flux densities dNT,L/dE add up to the total flux T + L. The high-temperature/low-frequency approximation (dot-dashed) of T + L is based on the first two orders of the ascending series in (3.4), the low-temperature/high-frequency asymptotics (dot-dot-dashed) is calculated from the two leading orders in (3.1). The unpolarized flux T + L is the actual spectral fit, the parameters of the electron density are recorded in Table 1.
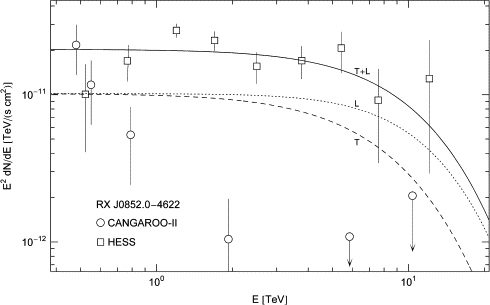
Fig. 2. Spectral map of SNR RX J0852.0−4622, data points from CANGAROO-II [25] and HESS [26]. The plots are labeled as in Fig. 1. T and L stand for the transversal and longitudinal flux components, and T+L labels the total unpolarized flux. Only the first two CANGAROO-II points (above the 10−11-mark) have been taken into account in the spectral fit. The CANGAROO and HESS data sets define different slopes, the CANGAROO slope is much steeper. γ-Ray observations of the Galactic center [27] and [28] also resulted in diverging slopes, cf. Fig. 4 in [28]. The HESS points and the two overlapping CANGAROO points define an extended spectral plateau in the high GeV range typical for cascade spectra, which is followed by exponential decay. The parameters of the inferred thermal electron density are listed in Table 1.
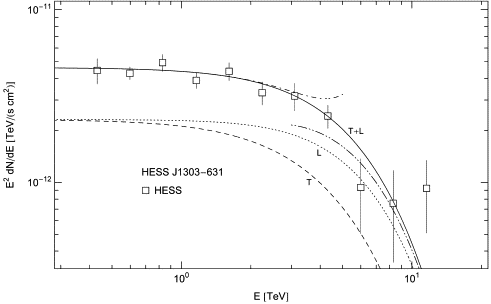
Fig. 3. Spectral map of the extended TeV γ-ray source HESS J1303−631. Data points from HESS [35]. The unpolarized spectral fit T + L is based on the electron density in Table 1, the polarized flux components are labeled T and L. The high- and low-temperature approximations of T + L are indicated by truncated dot-dashed and double-dot-dashed curves, respectively, with cross-over in the low TeV range. The electron populations producing the spectra in Fig. 1, Fig. 2 and Fig. 3 are thermal, the electron temperature is of the same order in all three sources, cf. Table 1. The spectral curvature is generated by the Boltzmann factor, cf. (3.1), the GeV plateau terminates in exponential decay without a power-law cross-over.
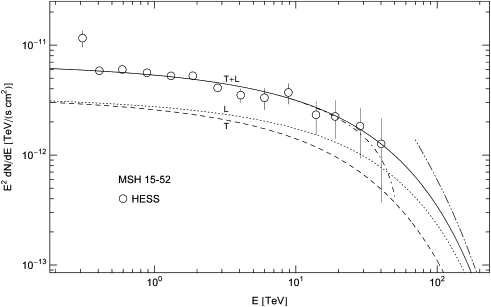
Fig. 4. Spectral map of the pulsar wind nebula in MSH
15-52. Data points from HESS [37]. The
tachyonic spectral fit (solid line T+L) is obtained with a non-thermal
electron distribution, cf. Table 1. The fit
is for unpolarized radiation and can be split into a transversally (T)
and longitudinally (L) polarized flux. The cutoff frequency of the
averaged radiation densities (T, L and T+L) is Ecut = (mt/m)kT ≈ 70 TeV,
defined by ![]() according to the low-temperature/high-frequency expansion (3.1). The high-
and low-temperature asymptotics of the unpolarized total flux T+L is
depicted by the dot-dashed and dot-dot-dashed curves. Most of the data
points lie in the high-temperature/low-frequency regime, contrary to Fig. 1, Fig. 2 and Fig. 3. The
decay in this regime is gradual but not power-law, with electron index α < 1,
cf. the discussion following (3.10).
according to the low-temperature/high-frequency expansion (3.1). The high-
and low-temperature asymptotics of the unpolarized total flux T+L is
depicted by the dot-dashed and dot-dot-dashed curves. Most of the data
points lie in the high-temperature/low-frequency regime, contrary to Fig. 1, Fig. 2 and Fig. 3. The
decay in this regime is gradual but not power-law, with electron index α < 1,
cf. the discussion following (3.10).
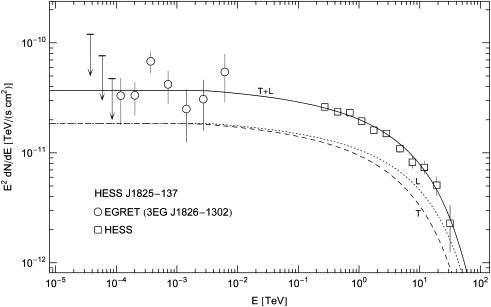
Fig. 5. Combined spectral map of the EGRET source 3EG J1826−1302 and the TeV source HESS J1825 − 137. Data points from EGRET [42] and HESS [41]. The solid line T+L is the spectral fit, T and L are the polarization components of the tachyon flux generated by a non-thermal electron density, cf. Table 1. The spectral break at E ≈ mtγ1 ≈ 3.4 GeV is barely visible as edge in the spectral map, cf. after (3.10), followed by exponential decay with electron index α ≈ 0.8 and cutoff frequency Ecut ≈ 40 TeV.
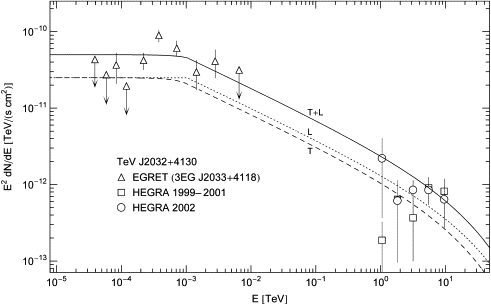
Fig. 6. Combined spectral map of the EGRET source 3EG J2033+4118 and the TeV source TeV J2032+4130. Data points from EGRET [42] and HEGRA [46]. A non-thermal electron population listed in Table 1 is inferred from the spectral fit T+L, obtained by adding the polarization components T and L. As the electron index exceeds 1, there emerges a power-law slope ∝E1−α, α ≈ 1.4, separating the GeV plateau from exponential decay. The spectral break between GeV plateau and power-law slope occurs at mtγ1 ≈ 1.0 GeV, cf. Table 1. The slope is nearly straight, the cutoff temperature of the electron density is too high (Ecut ≈ 160 TeV) to significantly curve the slope in the range covered by the TeV data points.
In the foregoing discussion of the high-temperature
asymptotics, we assumed an electron index α > 1.
We still have to settle the case α < 1.
The spectral peak at ωmax ≈ mt
is again determined by the factor ![]() .
Adjacent is a power-law slope
.
Adjacent is a power-law slope  pT,L
pT,L  α,β ∝ 1/ω
in the range 1
α,β ∝ 1/ω
in the range 1  ω/mt
ω/mt  1/β,
so that E2dNT,L/dE ∝ 1,
cf. (3.10). At ω ≈ mt/β,
there is the cross-over to exponential decay, cf. (3.1). This
holds true for γ1 = μ,
cf. (2.3), as well
as γ1
1/β,
so that E2dNT,L/dE ∝ 1,
cf. (3.10). At ω ≈ mt/β,
there is the cross-over to exponential decay, cf. (3.1). This
holds true for γ1 = μ,
cf. (2.3), as well
as γ1  1, provided βγ1
1, provided βγ1  1,
since the leading order of (3.4) does not
depend on γ for α < 1.
If βγ1
1,
since the leading order of (3.4) does not
depend on γ for α < 1.
If βγ1 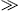 1 despite β being
small, then the low-temperature expansion (3.1) applies
instead of (3.4).
1 despite β being
small, then the low-temperature expansion (3.1) applies
instead of (3.4).
As the polarization is not observed, we add the transversal
and longitudinal densities, writing 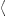 pT+L
pT+L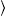
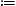
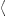 pT
pT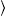 +
+ 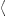 pL
pL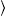 for
the energy density and NT+L
for
the energy density and NT+L 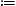 NT + NL
for the number flux, the spectral fits in Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5 and Fig. 6 are based
on the unpolarized differential flux, dNT+L/dE,
defined in (3.10). We
restore the natural units on the right-hand side of (3.10), up to
now we have used
NT + NL
for the number flux, the spectral fits in Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5 and Fig. 6 are based
on the unpolarized differential flux, dNT+L/dE,
defined in (3.10). We
restore the natural units on the right-hand side of (3.10), up to
now we have used 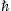 = c = 1,
and write E(1) for
= c = 1,
and write E(1) for 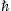 ω(1);
the plots in Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5 and Fig. 6 are in
TeV units, with dNT,L/dE
in units of TeV−1s−1cm−2.
The normalization factor in (2.12) is
dimensionless,
ω(1);
the plots in Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5 and Fig. 6 are in
TeV units, with dNT,L/dE
in units of TeV−1s−1cm−2.
The normalization factor in (2.12) is
dimensionless, ![]() ,
where n1 is the number of
radiating electrons with Lorentz factors exceeding γ1,
distributed according to density dρα,β
in (2.5). α
is the electronic power-law index, and β the
exponential cutoff in the electron spectrum, both to be determined from
the spectral fit like n1 and
γ1. As for the electron count
n1, it is convenient to use a
rescaled parameter
,
where n1 is the number of
radiating electrons with Lorentz factors exceeding γ1,
distributed according to density dρα,β
in (2.5). α
is the electronic power-law index, and β the
exponential cutoff in the electron spectrum, both to be determined from
the spectral fit like n1 and
γ1. As for the electron count
n1, it is convenient to use a
rescaled parameter ![]() for the fit,
for the fit,
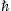 [keV
s] implies the tachyon mass in keV units, that is, we put mtc2 ≈ 2.15
in the spectral function (2.8). The
tachyon–electron mass ratio is mt/m ≈ 1/238,
cf. after (2.3). The
fitting procedure and in particular the spectral maps in Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5 and Fig. 6 are not
affected by the often uncertain distance estimate, in contrast to the
source count, cf. Table 1.
[keV
s] implies the tachyon mass in keV units, that is, we put mtc2 ≈ 2.15
in the spectral function (2.8). The
tachyon–electron mass ratio is mt/m ≈ 1/238,
cf. after (2.3). The
fitting procedure and in particular the spectral maps in Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5 and Fig. 6 are not
affected by the often uncertain distance estimate, in contrast to the
source count, cf. Table 1.
Electronic source densities generating the tachyonic spectral maps of the supernova remnants and TeV γ-ray sources in Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5 and Fig. 6
The electron densities dρα,β
in (2.5) are defined by parameters (α, β,
γ1, ![]() )
extracted from the spectral fit. α is the
electronic power-law index and β the cutoff
parameter in the Boltzmann factor. The lower edge of electronic Lorentz
factors in the source population is identified with the radiation
threshold, γ1 = μ,
cf. (2.3), except
for HESS J1825−137 and TeV J2032+4130.
)
extracted from the spectral fit. α is the
electronic power-law index and β the cutoff
parameter in the Boltzmann factor. The lower edge of electronic Lorentz
factors in the source population is identified with the radiation
threshold, γ1 = μ,
cf. (2.3), except
for HESS J1825−137 and TeV J2032+4130. ![]() is the amplitude of the tachyonic flux density, from which the electron
count ne is inferred, cf.
(3.11). d is the distance to the source, and kT
the electron temperature. The high-energy spectra of the SNRs G0.9+0.1
and RX J0852.0−4622 as well as the extended TeV source HESS J1303−631
are thermal, α = −2. The spectra
of the pulsar wind nebula MSH 15-52 and the TeV sources HESS J1825−137
and TeV J2032+4130 are power-law with exponential cutoff. The distance
estimates do not affect the spectral maps in Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5 and Fig. 6 but the
electronic source count ne.
The distances of RX J0852.0−4622, HESS J1303−631 and TeV J2032+4130
could be one order lower than the listed ones, references are given
after (3.11).
is the amplitude of the tachyonic flux density, from which the electron
count ne is inferred, cf.
(3.11). d is the distance to the source, and kT
the electron temperature. The high-energy spectra of the SNRs G0.9+0.1
and RX J0852.0−4622 as well as the extended TeV source HESS J1303−631
are thermal, α = −2. The spectra
of the pulsar wind nebula MSH 15-52 and the TeV sources HESS J1825−137
and TeV J2032+4130 are power-law with exponential cutoff. The distance
estimates do not affect the spectral maps in Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5 and Fig. 6 but the
electronic source count ne.
The distances of RX J0852.0−4622, HESS J1303−631 and TeV J2032+4130
could be one order lower than the listed ones, references are given
after (3.11).
Fig. 1 shows the high-energy spectral map of the composite SNR G0.9+0.1 [22], [23] and [24] in the Galactic center, at a distance of 10 kpc [23] and [24]. The core component is presumably a pulsar wind nebula, though no pulsed emission has yet been detected.
In Fig. 2, we show the tachyonic spectral map of the shell-type SNR RX J0852.0−4622 [25], [26], [27], [28], [29], [30], [31], [32], [33] and [34]. The 1.157 MeV line of the short-lived 44Ti isotope (with a half-life of 60 yr) was detected by COMPTEL, and an age of 700 years and a distance of 0.2 kpc was inferred [29], [30] and [34]. This detection, however, was marginal [32], and column density estimates suggest a distance of 1–2 kpc, in the direction of and probably associated with the Vela Molecular Ridge [30]. A compact X-ray source has been located near the SNR center [32] and [33].
The spectrum of the extended TeV source HESS J1303−631 [35] is depicted in Fig. 3. The distance of 15.8 kpc is inferred from an association with PSR J1301−6305 [36], but could be one order smaller, since associations with other pulsars or molecular clouds at much smaller distance are possible [35].
In Fig. 4, we plot the spectral map of the pulsar wind nebula in MSH 15-52 [37], [38], [39] and [40]. The nebula is powered by PSR B1509−58 [38] and [39], located at a distance of 4.4 kpc [40].
The spectrum of the TeV source HESS J1825−137 [41], [42], [43] and [44] is shown in Fig. 5. This source is associated with the EGRET source 3EG J1826−1302 [41], which is believed to be powered by PSR B1823−13 [43]. A further association of this pulsar with HESS J1825−137 is suggested by the one-sided X-ray morphology of the asymmetric pulsar wind nebula G18.0−0.7 powered by PSR B1823−13 [44], since the TeV emission of HESS J1825−137 is likewise strongly one-sided [41]. The distance estimate for PSR B1823−13 is 4.1 kpc [40].
Fig. 6 shows the spectral map of the presumably extended TeV source TeV J2032+4130 [45], [46], [47] and [48], associated with the EGRET source 3EG J2033+4118 [45]. The distance estimate is 15 kpc, inferred from an association with the low-mass X-ray binary 4U 1624–49 [47] and [48]. However, TeV J2032+4130 could be as close as 1.7 kpc if located in the Cyg OB2 association [45] and [46].
Once ![]() is extracted from the spectral fit, we calculate via (3.11) the
number of radiating electrons n1
constituting the density dρα,β.
This, however, implies that all tachyons reaching the detector are
properly counted. At γ-ray energies, only a tiny αq/αe-fraction
(the ratio of tachyonic and electric fine structure constants, αq/αe ≈ 1.4 × 10−11)
of the tachyon flux is actually absorbed [49] and [50]. This
requires a rescaling of the electron count n1,
so that the actual number of radiating electrons is ne
is extracted from the spectral fit, we calculate via (3.11) the
number of radiating electrons n1
constituting the density dρα,β.
This, however, implies that all tachyons reaching the detector are
properly counted. At γ-ray energies, only a tiny αq/αe-fraction
(the ratio of tachyonic and electric fine structure constants, αq/αe ≈ 1.4 × 10−11)
of the tachyon flux is actually absorbed [49] and [50]. This
requires a rescaling of the electron count n1,
so that the actual number of radiating electrons is ne 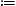 n1αe/αq ≈ 7.3 × 1010
n1. (This rescaling applies
to γ-ray spectra only, to frequencies much higher
than the 2 keV tachyon mass, so that the mass-square can be
dropped in the tachyonic dispersion relation. At X-ray energies, we
have to rescale with the respective cross-section ratio, σe(ω)/σq
(ω), where σe
is the electromagnetic cross-section and σq
its tachyonic counterpart [7].) In Table 1, we list
the flux amplitude
n1αe/αq ≈ 7.3 × 1010
n1. (This rescaling applies
to γ-ray spectra only, to frequencies much higher
than the 2 keV tachyon mass, so that the mass-square can be
dropped in the tachyonic dispersion relation. At X-ray energies, we
have to rescale with the respective cross-section ratio, σe(ω)/σq
(ω), where σe
is the electromagnetic cross-section and σq
its tachyonic counterpart [7].) In Table 1, we list
the flux amplitude ![]() inferred from the spectral fit, as well as the renormalized electron
count ne depending on the
distance estimate. The density dρα,β
is defined by parameters
inferred from the spectral fit, as well as the renormalized electron
count ne depending on the
distance estimate. The density dρα,β
is defined by parameters ![]() obtained from the spectral fit. For instance, the source count in the
surface field of PSR B1509−58 is ne ≈ 1.3 × 1047
[49], to be
compared to 8.3 × 1047
obtained here for the pulsar wind nebula in MSH 15-52, cf. Table 1.
obtained from the spectral fit. For instance, the source count in the
surface field of PSR B1509−58 is ne ≈ 1.3 × 1047
[49], to be
compared to 8.3 × 1047
obtained here for the pulsar wind nebula in MSH 15-52, cf. Table 1.
4. Conclusion
We have studied superluminal radiation from electrons in uniform motion. Tachyonic synchrotron and cyclotron radiation were investigated in [17]. In the zero-magnetic-field limit, the tachyonic synchrotron densities converge to the spectral densities (2.1) for uniform motion. Orbital curvature induces modulations in the spectral densities. At μG-field strengths as encountered in the shock-heated plasmas of SNRs, these oscillations are quite small, just tiny ripples along the slope of densities (2.1) with increasing amplitude toward the spectral break. If integrated over a thermal or power-law electron population, the oscillations are averaged out, so that the spectral densities (2.12) can still be used for electron trajectories bent by weak magnetic fields. As discussed in the Introduction, the source particles radiate in uniform motion, there is no electromagnetic radiation damping unless the trajectories spiral through magnetic fields. The energy radiated is drained from the absorber breaking the time symmetry of the Green function outside the lightcone.
We averaged the superluminal flux densities with electronic
source distributions, derived the high- and low-temperature expansions
of the spectral averages, and explained the spectral plateaus, the
power-law slopes and the curvature of the spectral maps. We
demonstrated that the γ-ray spectra of the
supernova remnants and TeV sources listed in Table 1 can be
reproduced by tachyonic cascade spectra. Speed and energy of tachyonic
quanta are related by 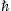 ω = mtc2(υ2/c2 − 1)−1/2.
At γ-ray energies, their speed is close to the
speed of light, the basic difference to electromagnetic radiation is
the longitudinally polarized flux component. The polarization of
tachyons can be determined from transversal and longitudinal ionization
cross-sections, which peak at different scattering angles [51].
ω = mtc2(υ2/c2 − 1)−1/2.
At γ-ray energies, their speed is close to the
speed of light, the basic difference to electromagnetic radiation is
the longitudinally polarized flux component. The polarization of
tachyons can be determined from transversal and longitudinal ionization
cross-sections, which peak at different scattering angles [51].
The source numbers listed in Table 1 are
lower bounds based on γ-ray emission only. The tachyonic fine structure
constant enters as a square in the number count, once via (3.11) when
inferring the preliminary count n1
from the spectral fit, and a second time when rescaling this count to
obtain the actual source number ![]() .
The tachyonic fine structure constant is an independent estimate from
Lamb shifts in hydrogenic ions [5], it enters
only linearly in the spectral density (2.1), in
contrast to the squared electromagnetic constant in the Klein–Nishina
cross section. The cutoff in the electron energy is much higher
compared to a Compton fit, which compensates the small tachyonic fine
structure constant in the spectral density and the absorption
probability, as well as the reduced source count.
.
The tachyonic fine structure constant is an independent estimate from
Lamb shifts in hydrogenic ions [5], it enters
only linearly in the spectral density (2.1), in
contrast to the squared electromagnetic constant in the Klein–Nishina
cross section. The cutoff in the electron energy is much higher
compared to a Compton fit, which compensates the small tachyonic fine
structure constant in the spectral density and the absorption
probability, as well as the reduced source count.
Source counts based on Compton fits have not yet been calculated for the sources discussed here, but one can obtain a rough estimate if one considers the Compton count for the Crab Nebula and rescales with the observed TeV power ratio. To this end, we use the total TeV flux of the respective source in Crab units, such as F/FCrab ≈ 0.02 for SNR G0.9+0.1, cf. [22]. The flux of SNR RX J0852.0−4622 is roughly that of the Crab [26]. A flux ratio of 0.17 for HESS J1303−631 is quoted in [35], and a ratio of 0.15 for MSH 15-52 in [37]. The TeV flux of HESS J1825−137 is a 0.68 fraction of the Crab [41], and the flux collected from TeV J2032+4130 amounts to 5% of the Crab flux [46]. The power ratio is obtained as P/PCrab ≈ (d2[kpc]/4)F/FCrab, with 2 kpc to the Crab. The distance estimates of the respective sources are listed in Table 1.
A count of nCrab ≈ 1.3 × 1051 electrons/positrons in the Crab was derived from an electromagnetic inverse-Compton model in [52]. An estimate of the Compton count for the above sources is found by rescaling with the power ratio. We obtain nCrabP/PCrab ≈ 3.7 × 1051 both for HESS J1825−137 and TeV J2032+4130 (based on the distance estimates in Table 1); the estimates for the other sources are similar within one order of magnitude. The counts based on the tachyonic cascade fits in Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5 and Fig. 6 are two to three orders lower than the respective Compton count, cf. Table 1. In either case, the distance estimate enters as a square, which can lower the source count of RX J0852.0−4622, HESS J1303−631 and TeV J2032+4130 by two orders, cf. after (3.11).
Apart from the extended plateaus in the spectral maps, it is the high cutoff in the electron energy rather than the mildly reduced source count that distinguishes tachyonic cascade spectra from inverse-Compton fits and, for that matter, hadronic radiation models based on pion decay [53] and [54]. In the case of a thermal electron distribution, with electron index α = −2, we may identify kT[TeV] ≈ 5.11 × 10−7/β, cf. (2.5). We use this definition of electron temperature also for other electron indices; kT is the energy at which the exponential decay of the electron density sets in, cf. the end of Appendix A. The TeV spectra discussed here show significant curvature, and we demonstrated that this curvature is reproduced by an exponentially cut power-law electron distribution. The exponential shows in the low-temperature/high-frequency expansion of the averaged spectral density, cf. (2.12) and (3.1), curving the spectral slopes in double-logarithmic plots. This curvature is intrinsic, there is no attenuation owing to infrared background photons, as tachyons do not interact with electromagnetic radiation fields. Besides, the sources discussed here are all Galactic; tachyonic spectral maps of TeV blazars are studied in [55]. The cutoff kT in the electron energy listed in Table 1 is to be compared to the spectral breaks in the cosmic-ray spectrum. These breaks occur at about 103.5, 105.8 and 107 TeV, dubbed knee, second knee and ankle, respectively [56]. In MSH 15-52 as well as HESS J1825−137 and TeV J2032+4130, the cutoff happens between the first and second knee. As for protonic source particles, the cutoff energies kT in Table 1 have to be multiplied with 1.8 × 103, the proton/electron mass ratio, so that we arrive beyond the ankle, at protons in the 1021 eV range, which suggests Galactic TeV γ-ray sources as production sites of ultra-high-energy cosmic rays. In this case, the tachyon/electron mass ratio in the spectral densities has to be replaced by mt/mp ≈ 2.3 × 10−6, cf.(2.1), (2.2), (2.3), (2.4), (2.5), (2.6), (2.7), (2.8), (2.9), (2.10) and (2.11). In Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5 and Fig. 6, however, this is not necessary, since even the tachyon/electron ratio is too small to noticeably affect the spectral maps.
Acknowledgments
The author acknowledges the support of the Japan Society for the Promotion of Science. The hospitality and stimulating atmosphere of the Centre for Nonlinear Dynamics, Bharathidasan University, Trichy, and the Institute of Mathematical Sciences, Chennai, are likewise gratefully acknowledged.
References
Appendix A. Asymptotic normalization of the electronic source densities
We derive the low- and high-temperature expansions of the
normalization factors Aα,β(γ1,n1)
of densities (2.5),
 γ
γ  ∞.
∞.
A.1. Low-temperature expansion of Kα,β(γ1)
To obtain the low-temperature expansion of Kα,β(γ1 = 1),
we substitute γ = x + 1
in the integrand of (A.1), and then
expand in x except for the exponential. Using
term-by-term integration (via Watson’s Lemma), we readily find
This expansion apparently applies if
with the asymptotic series Kα,β(1) in (A.2). As for kα,β(γ1), we write γ = 1 + δx, where δ
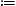 γ1 − 1,
and expand the integrand in an ascending series in x,
except for the exponential. Term-by-term integration gives a
power-series in δ,
γ1 − 1,
and expand the integrand in an ascending series in x,
except for the exponential. Term-by-term integration gives a
power-series in δ,where we use the shortcut
with positive half-integer j. This high-temperature expansion of Kα,β(γ1), defined by (A.4) with series (A.2) and (A.5) substituted, is applicable if β
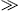 1 and δ
1 and δ 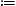 γ1 − 1
γ1 − 1  1,
so that βδ is small. If βδ is
large, the expansion of Kα,β(γ1)
in (A.3) applies.
As mentioned, series (A.3) can be
used in the high-temperature regime, β
1,
so that βδ is small. If βδ is
large, the expansion of Kα,β(γ1)
in (A.3) applies.
As mentioned, series (A.3) can be
used in the high-temperature regime, β  1,
provided βγ1
1,
provided βγ1 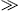 1.
1.
A.2. High-temperature expansion of Kα,β(γ1)
We write Kα,β(γ1)
in (A.1) as
where we put a = α + 2n,
Here, we substitute the ascending series
interchange the summations, and substitute
In this way, we find the ascending β-expansion of Kα,β(γ1) as
where
It remains to find a more tractable expression for fα,β (γ1). To this end, we return to the integral kα,β(γ1) in (A.4). Expanding the exponential, the term-by-term integration is effected by
We write b = α − k, and find
The series (A.16) is identical with (A.13), by virtue of
We thus find
The coefficients in (A.20) are those of the root in (A.7). The notation Kα,β(0) and kα,β(∞) symbolizes the respective integrals in (A.7) and (A.4), with the exponential or root formally expanded. The high-temperature expansion of Kα,β(γ1), defined by (A.12) and (A.16), is efficient for βγ1
 1,
provided γ1 is not too close
to one. If βγ1
1,
provided γ1 is not too close
to one. If βγ1 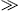 1, we use the expansion of Kα,β(γ1)
in (A.3) instead.
The high-temperature expansion of Kα,β(1)
is defined by (A.19), (A.20) and (A.21). There
are singularities for integer α, which cancel in
every order if ε-expanded, cf. Appendix B.
1, we use the expansion of Kα,β(γ1)
in (A.3) instead.
The high-temperature expansion of Kα,β(1)
is defined by (A.19), (A.20) and (A.21). There
are singularities for integer α, which cancel in
every order if ε-expanded, cf. Appendix B.
If γ1 ≈ 1,
we use
This series is recovered from (A.15), by substituting into (A.16) the identity [21]
with b = α−k. The series (A.23) can also directly be obtained from (A.4); we expand the exponential and use the variable substitution y = γ2 − 1 and the integral representation
The calculation of Kα,β(γ1) via (A.22) and (A.23) is efficient for γ1 close to one, such as γ1 = μ, cf. after (2.5).
We discuss the location of the peak of the densities dρα,β(γ)
in (2.5). γmax is determined
as the γ > 1 zero of γ3 + (α/β)γ2−γ−(α + 1)
/β = 0. We give only the leading
orders and state the expansion parameters. If β 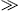 1, we find γmax = 1 + 1/(2β) + O(β−2).
If β
1, we find γmax = 1 + 1/(2β) + O(β−2).
If β  1
and α < 0, we find γmax = −(α/β)(1 + O(β2/α3)),
from the third and second order. In leading order, the ‘displacement
law’ βγmax ≈ const
holds true; the expansion parameter is stated in the preceding O-term.
If β
1
and α < 0, we find γmax = −(α/β)(1 + O(β2/α3)),
from the third and second order. In leading order, the ‘displacement
law’ βγmax ≈ const
holds true; the expansion parameter is stated in the preceding O-term.
If β  1
and α > 0,
1
and α > 0, ![]() ,
via the zeroth and second order; this peak is followed by a power-law
slope γ−α,
extending to γ ≈ 1/β.
Finally, if β
,
via the zeroth and second order; this peak is followed by a power-law
slope γ−α,
extending to γ ≈ 1/β.
Finally, if β  1
and α very close to zero, we may still have β/
1
and α very close to zero, we may still have β/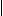 α
α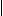 3/2
3/2 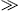 1, so that the indicated expansions
break down. In this case, we find γmax = β−1/3(1 + O(β2/3,
α/β3/2)),
from the zeroth and third order, where the O-term stands for a double
series in the indicated parameters.
1, so that the indicated expansions
break down. In this case, we find γmax = β−1/3(1 + O(β2/3,
α/β3/2)),
from the zeroth and third order, where the O-term stands for a double
series in the indicated parameters.
Appendix B. ε-expansion of the normalization factors Kα,β(γ1) at integer electron index α
We need two ε-expansions of the Γ-function,
that of Γ(−n + ε)
in (3.6) and
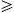 0.
At n = 0, the series
2(1 + 1/3 + …) is dropped. We at
first give the ε-expansion of Kα,β(1)
in (A.19). To this
end, we decompose
0.
At n = 0, the series
2(1 + 1/3 + …) is dropped. We at
first give the ε-expansion of Kα,β(1)
in (A.19). To this
end, we decomposeand the series κ1,2 read
obtained by splitting kα,β(∞) = κ1 + κ2 in (A.21). We substitute α = m + ε, where m is an integer at which the series become singular. We then expand in ε, making use of the ε-expansions of the Γ-function in (3.6) and (B.1). The ε-poles cancel if the series are added according to (B.2). The following expansions of Kα,β(0) and κ1,2 are valid up to terms of O(ε).
We start by expanding Kα,β(0)
in (B.3). We put α = 2k + ε
and find, for k 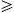 1,
1,
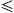 0,
this is replaced by
0,
this is replaced byThe poles at odd integers are dealt with in like manner. We put α = 2k + 1 + ε and find, for k
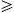 0,
0,and for k
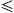 −1,
−1,We turn to the ε-expansion of series κ1,2
in (B.4) and (B.5). Series κ1
is singularity free and even finite at even integer α,
so that we can use (B.4) at α = 2k.
(The series terminates when the Γ-functions in the
denominator become singular.) Series κ2
is singular at even integers. We substitute α = 2k + ε
and expand, arriving at
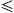 1,
and at
1,
and atfor k
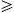 2.
2.
Finally, we consider the series κ1,2
at odd integer α. We put α = 2k + 1 + ε
and find, for k  0,
0,
 1,
1,Series κ2 is finite and singularity free at odd integer α, so that we can use (B.5) at α = 2k + 1.
Thus, at integer α, we can piece together
series Kα,β(1)
in (B.2) by adding
the respective series in (B.4), (B.5), (B.6), (B.7), (B.8), (B.9), (B.10), (B.11), (B.12) and (B.13). For
instance, K−2,β(1) = K2(β)/β,
with the modified Bessel function K2,
which follows by putting k = −1
and adding Kα,β(0)
in (B.7), κ1
in (B.4) (with α = 2k),
and κ2 in (B.10). There
are no singularities in the first two orders of Kα,β(1)
for α  3
and α
3
and α  −2,
so that we can read them off from (A.19), (A.20) and (A.21). In
between, we find the leading orders at integer α as
−2,
so that we can read them off from (A.19), (A.20) and (A.21). In
between, we find the leading orders at integer α as
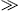 1, we calculate these functions via (A.24). However,
in (A.24) there
occur singularities at α−k = b = −(2m + 1),
m
1, we calculate these functions via (A.24). However,
in (A.24) there
occur singularities at α−k = b = −(2m + 1),
m 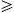 −1.
In this case, we calculate the hypergeometric functions in (A.23) by means
of the identity
−1.
In this case, we calculate the hypergeometric functions in (A.23) by means
of the identityAt any other integer b = α − k, we can use (A.24), as it is singularity free.
We finally indicate the derivation of (B.15), obtained
by ε-expansion of (A.24). We start
with the series (A.17);
singularities occur at b = −(2m + 1) + ε,
m 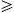 −1.
We find,
−1.
We find,
Identity (B.15) follows by substituting expansions (B.16) and (B.17) into (A.24).