Roman Tomaschitz 2014 EPL 106 39001
doi:10.1209/0295-5075/106/39001
Copyright © EPLA, 2014
Received 3 February 2014,
accepted for publication 22 April 2014
Published 15 May 2014
View usage and citation metrics for this article Get permission to re-use this article
Tachyonic Cherenkov fits are performed to the Fermi-LAT γ-ray spectra of the Vela pulsar, PSR J1709 − 4429 and Geminga. The high-energy spectral tails of these pulsars exhibit pronounced subexponential Weibull decay, which can be modeled in a permeable spacetime by a frequency-dependent tachyon mass. The scaling exponent of the tachyon mass defines the Weibull shape parameter of the energy flux, and it also determines whether the radiation is sub- or superluminal. The negative mass-square in the tachyonic Maxwell-Proca equations gives rise to a longitudinal flux component. The radiation is generated by an ultra-relativistic thermal electron plasma via the inertial Cherenkov effect. The transversal and longitudinal γ-ray emission from Geminga is slightly superluminal, whereas γ-rays from the Vela pulsar and PSR J1709 − 4429 are subluminal despite the negative tachyonic mass-square in the dispersion relations.
In the 2nd Fermi-LAT pulsar catalog [1], the energy flux of several pulsars shows weaker-than-exponential decay in the low GeV band, for instance, the Vela pulsar (PSR J0835 − 4510) [2] and PSR J1709 − 4429 [3], as well as the Crab pulsar (PSR J0534 + 2200) [4], PSR J1836 + 5925 [5], Geminga (PSR J0633 + 1746) [6], and PSR J2021 + 4026 [7]. The subexponential decay of the γ-ray spectral tails can be explained by tachyonic Cherenkov emission from a thermal electron plasma.
First,
we briefly outline the radiation mechanism, the coupling of tachyonic
radiation fields to a dispersive permeability tensor, the Maxwell-Proca
equations with negative mass-square, the Lagrangian and the dispersion
relations, all in space-frequency representation suitable for
frequency-dependent permeabilities, cf. (1)–(7).
We discuss the tachyonic Cherenkov densities generated by a uniformly
moving subluminal charge in a dispersive spacetime and explain the
frequency scaling of the tachyon mass and the tachyonic fine-structure
constant, cf. (8)–(13).
We average the spectral densities with relativistic electron
distributions and derive the transversal and longitudinal polarization
components of the tachyonic energy flux, cf. (14)–(25). We study the high- and intermediate-energy regimes, in particular the Weibull decay 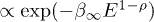 of the spectral tail, where ρ is the scaling exponent of the tachyon mass,
of the spectral tail, where ρ is the scaling exponent of the tachyon mass, 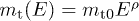 , and
, and 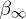 is a decay constant related to the electron temperature and the tachyonic mass amplitude
is a decay constant related to the electron temperature and the tachyonic mass amplitude 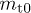 , cf. (26)–(30).
We perform spectral fits to the Fermi-LAT spectra of the Vela pulsar,
PSR J1709 − 4429 and Geminga, extracting the scaling exponents
of the tachyon mass and the tachyonic fine-structure constant, cf.
figs. 1–3, and explain how sub- and superluminal group velocities in the γ-ray band are related to the Weibull shape parameter, cf. (31).
, cf. (26)–(30).
We perform spectral fits to the Fermi-LAT spectra of the Vela pulsar,
PSR J1709 − 4429 and Geminga, extracting the scaling exponents
of the tachyon mass and the tachyonic fine-structure constant, cf.
figs. 1–3, and explain how sub- and superluminal group velocities in the γ-ray band are related to the Weibull shape parameter, cf. (31).
Fig. 1: (Colour on-line) Tachyonic γ-ray spectrum of the Vela pulsar. Data points from Fermi-LAT (Large Area Telescope, 2nd Pulsar Catalog) [1]. The solid curve 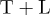 depicts the unpolarized tachyonic energy flux
depicts the unpolarized tachyonic energy flux 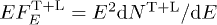 , cf. (22) and (25), obtained by adding the transversal flux component
, cf. (22) and (25), obtained by adding the transversal flux component 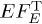 (dotted curve, labeled T) and the longitudinal component
(dotted curve, labeled T) and the longitudinal component 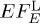 (dashed curve, L). The polarization components
(dashed curve, L). The polarization components 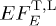 are compiled in (20)–(22). The dot-dashed and double-dot–dashed curves depict the asymptotic limits of
are compiled in (20)–(22). The dot-dashed and double-dot–dashed curves depict the asymptotic limits of 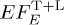 ; the power-law ascent (28) is followed by a cross-over into subexponential Weibull decay, cf. (26) and table 1. (7 dof,
; the power-law ascent (28) is followed by a cross-over into subexponential Weibull decay, cf. (26) and table 1. (7 dof, 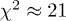 .)
.)
We summarize the basic equations to keep the paper self-contained; details can be found in [8,9]. The Fourier time-transform of the tachyonic vector potential 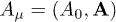 is defined by
is defined by 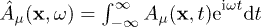 , and the same convention applies for field strengths, inductions and currents. The homogeneous Maxwell equations read
, and the same convention applies for field strengths, inductions and currents. The homogeneous Maxwell equations read 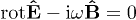 ,
, 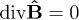 . The field strengths
. The field strengths 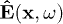 and
and 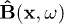 are related to the vector potential by
are related to the vector potential by 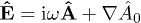 ,
, 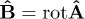 . The constitutive relations defining the inductions
. The constitutive relations defining the inductions 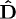 and
and 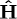 and the inductive potential
and the inductive potential 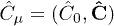 are
are
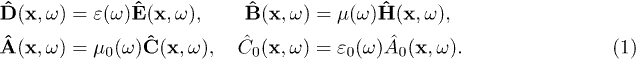
The permeabilities ε, 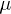 ,
, 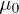 and
and 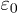 are positive and dimensionless. As the inductions are real, the permeabilities satisfy
are positive and dimensionless. As the inductions are real, the permeabilities satisfy 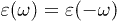 , etc. In vacuum,
, etc. In vacuum, 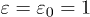 and
and 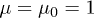 (Heaviside-Lorentz system). The inhomogeneous field equations coupled to a current
(Heaviside-Lorentz system). The inhomogeneous field equations coupled to a current 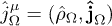 , cf. after (5), read
, cf. after (5), read
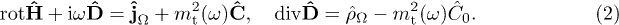
We take the divergence of the first equation, substitute the second and use current conservation 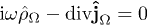 to obtain the Lorentz condition
to obtain the Lorentz condition 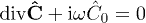 , due to the tachyonic mass-square
, due to the tachyonic mass-square 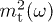 . (
. (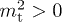 with the sign convention in (2) and (3).) The energy flux vector is
with the sign convention in (2) and (3).) The energy flux vector is 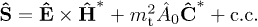 The field equations can be derived from the Lagrangian
The field equations can be derived from the Lagrangian
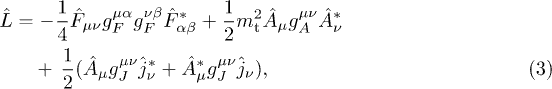
where 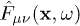 is the Fourier transform of the field tensor
is the Fourier transform of the field tensor 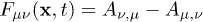 .
The tachyonic radiation field is modeled after electrodynamics, a Proca
field with negative mass-square, minimally coupled to an electron
current in a dispersive spacetime, the Minkowski metric being replaced
by permeability tensors
.
The tachyonic radiation field is modeled after electrodynamics, a Proca
field with negative mass-square, minimally coupled to an electron
current in a dispersive spacetime, the Minkowski metric being replaced
by permeability tensors 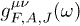 .
A space-frequency representation is employed to avoid clumsy time
convolutions of the inductive fields. The first term in (3) containing
.
A space-frequency representation is employed to avoid clumsy time
convolutions of the inductive fields. The first term in (3) containing 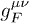 is analogous to the electrodynamic Lagrangian in a dielectric medium,
in manifestly covariant notation. A second permeability tensor
is analogous to the electrodynamic Lagrangian in a dielectric medium,
in manifestly covariant notation. A second permeability tensor 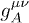 enters in the mass term, resulting in different dispersion relations
and group velocities for transversal and longitudinal modes, cf. (4) and (7). The meaning of permeability tensor
enters in the mass term, resulting in different dispersion relations
and group velocities for transversal and longitudinal modes, cf. (4) and (7). The meaning of permeability tensor 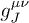 in the interaction term is explained after (5).
in the interaction term is explained after (5).
Fig. 2: (Colour on-line) Tachyonic energy flux of pulsar PSR J1709 − 4429. Data points from Fermi-LAT [1]. Description of the curves as in fig. 1; the fitting parameters are listed in table 1.
The transversal radiation is linearly polarized and weaker than the
longitudinal component. The spectral shape and parameters are similar to
the Vela spectrum in fig. 1, apart from the lower flux amplitude partially due to the increased distance 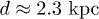 (
(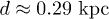 for the Vela pulsar). (7 dof,
for the Vela pulsar). (7 dof, 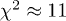 .)
.)
Fig. 3: (Colour on-line) Tachyonic spectral map of Geminga. Data points from Fermi-LAT [1]. Description of the curves as in fig. 1. The ascending slope is steeper than in figs. 1 and 2, since the fine-structure scaling exponent σ is close to zero, cf. table 1. The mass scaling exponent ρ lies below 1/2, which results in a rapid spectral cutoff, cf. (26), and renders the radiation superluminal, cf. (31). The distance estimate is 0.25 kpc. (7 dof, 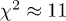 .)
.)
A
distinct difference of tachyonic Cherenkov radiation as compared to
electromagnetic radiation, Cherenkov, synchrotron or otherwise, is the
potential sub- or superexponential decay of γ-ray spectral
tails, once the spectral densities are averaged over a thermal or
non-thermal electron distribution. In contrast, electromagnetic
radiation mechanisms lead to strictly linear exponential decay of the
averaged spectral densities. The subexponential Weibull decay 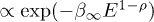 (see the introduction) observed in the spectral tails of the mentioned pulsars is pronounced, the power-law exponents ρ listed in table 1 substantially differ from zero. It would not be possible to fit the γ-ray spectra in figs. 1–3
with a logarithmic correction to a linear exponential. The conceptually
most important difference to electromagnetic radiation is
superluminality, which arises for
(see the introduction) observed in the spectral tails of the mentioned pulsars is pronounced, the power-law exponents ρ listed in table 1 substantially differ from zero. It would not be possible to fit the γ-ray spectra in figs. 1–3
with a logarithmic correction to a linear exponential. The conceptually
most important difference to electromagnetic radiation is
superluminality, which arises for 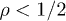 due to the tachyonic mass-square. If the decay is weak,
due to the tachyonic mass-square. If the decay is weak, 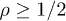 , the velocity of the radiated quanta is subluminal despite the mass term in (3). Here, we show how the shape parameter
, the velocity of the radiated quanta is subluminal despite the mass term in (3). Here, we show how the shape parameter 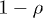 of tachyonic Cherenkov spectra can be used to distinguish subluminal from superluminal group velocities of γ-rays close to the speed of light.
of tachyonic Cherenkov spectra can be used to distinguish subluminal from superluminal group velocities of γ-rays close to the speed of light.
Another marked difference to electromagnetic spectra owing to the tachyonic mass-square in Lagrangian (3) is longitudinal polarization. Especially in the classical Cherenkov regime, where the tachyon-electron mass ratio is small, 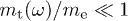 , there is a substantial longitudinal radiation component, see figs. 1–3,
and the weaker transversal radiation is linearly polarized, that is,
there is only one degree of transversal polarization. If one just uses
Stokes parameters to analyze the polarization, one will mistakenly
identify the longitudinal component as transversal, as these parameters
are based on the assumption of transversality. In the extreme quantum
regime, where
, there is a substantial longitudinal radiation component, see figs. 1–3,
and the weaker transversal radiation is linearly polarized, that is,
there is only one degree of transversal polarization. If one just uses
Stokes parameters to analyze the polarization, one will mistakenly
identify the longitudinal component as transversal, as these parameters
are based on the assumption of transversality. In the extreme quantum
regime, where 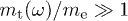 (which can be reached in TeV spectra because of the frequency
dependence of the tachyon mass), there emerge two transversal degrees of
comparable magnitude as well as a weaker longitudinal radiation
component, but this is not the case for the pulsar spectra discussed
here.
(which can be reached in TeV spectra because of the frequency
dependence of the tachyon mass), there emerge two transversal degrees of
comparable magnitude as well as a weaker longitudinal radiation
component, but this is not the case for the pulsar spectra discussed
here.
The 3D field strengths are 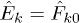 and
and 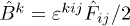 . The Fourier transform of the 4-current
. The Fourier transform of the 4-current 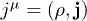 is denoted by
is denoted by 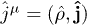 in Lagrangian (3). The permeabilities in (1) define isotropic tensors
in Lagrangian (3). The permeabilities in (1) define isotropic tensors 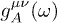 and
and 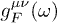 ,
,
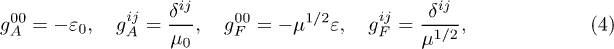
with 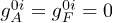 . The permeability tensor
. The permeability tensor 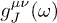 couples the external current to the field,
couples the external current to the field,
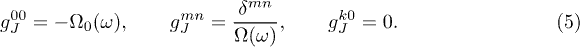
Greek indices are raised and lowered with the Minkowski metric 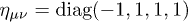 . The inductive 4-potential is
. The inductive 4-potential is 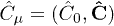 or
or 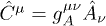 , and the inductive field tensor reads
, and the inductive field tensor reads 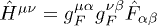 . The inductions in (1) are related to
. The inductions in (1) are related to 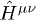 by
by 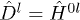 and
and 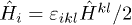 .
.
Table 1:.
Fitting parameters of the tachyonic energy flux of the pulsars in figs. 1–3. Recorded are the fine-structure scaling exponent 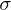 and the scaling exponent ρ of the tachyon mass, cf. (10) and (26), the decay exponent
and the scaling exponent ρ of the tachyon mass, cf. (10) and (26), the decay exponent 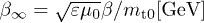 , cf. (17) and (27), and the flux amplitude
, cf. (17) and (27), and the flux amplitude 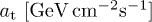 , cf. (24). The spectral fits are based on the differential flux density
, cf. (24). The spectral fits are based on the differential flux density 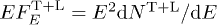 , cf. (25). The γ-rays are radiated by a thermal ultra-relativistic plasma with electron index
, cf. (25). The γ-rays are radiated by a thermal ultra-relativistic plasma with electron index  .
.
| σ | ρ |  |
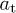 |
|
| Vela | –0.443 | 0.543 | 2.404 | 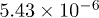 |
| J1709 | –0.558 | 0.611 | 2.743 | 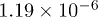 |
| Geminga | –0.0186 | 0.444 | 2.159 | 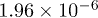 |
The "dressed" current 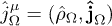 in the field equations (2) is defined by
in the field equations (2) is defined by 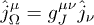 , cf. (3). The tensor
, cf. (3). The tensor 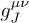 amounts to a varying coupling constant if
amounts to a varying coupling constant if 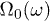 coincides with
coincides with 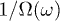 [9], which is assumed in the following, cf. (10) and table 1. Thus,
[9], which is assumed in the following, cf. (10) and table 1. Thus, 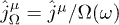 or
or 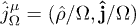 . If the external current is conserved,
. If the external current is conserved, 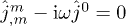 , this holds true for
, this holds true for 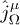 as well, so that the field equations for the vector potential read
as well, so that the field equations for the vector potential read
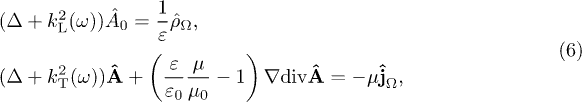
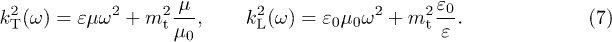
The Proca equations (6) and dispersion relations (7) are equivalent to the Maxwell equations (2) with conserved current. Transversal waves satisfy 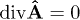 , longitudinal ones
, longitudinal ones 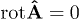 .
.
We consider a classical charge q moving with constant subluminal velocity 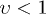 . The charge and current densities are
. The charge and current densities are 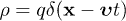 and
and 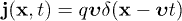 . In [9], we calculated the tachyonic radiation fields of this current via the Proca equations (6) and (7), and derived the asymptotic Poynting vectors and the power
. In [9], we calculated the tachyonic radiation fields of this current via the Proca equations (6) and (7), and derived the asymptotic Poynting vectors and the power 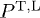 transversally and longitudinally radiated:
transversally and longitudinally radiated:
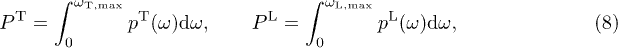
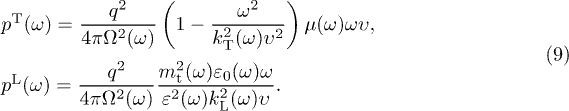
The integration of the classical densities in (8) is over frequency intervals in which 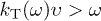 and
and 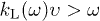 respectively, cf. (7). Here, we assume that equation
respectively, cf. (7). Here, we assume that equation 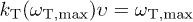 has just one solution and
has just one solution and 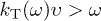 for
for 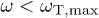 , and analogously for the longitudinal power
, and analogously for the longitudinal power 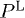 and
and 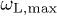 . We will consider constant positive permeabilities with
. We will consider constant positive permeabilities with 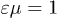 and
and 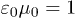 , so that the transversal and longitudinal dispersion relations (7) coincide. Radiation from uniformly moving subluminal charges is generated by the Cherenkov mechanism [10,11]. The radiated tachyonic quanta can be sub- or superluminal, cf. (31).
Apart from the inertial Cherenkov effect, electromagnetic radiation by
transversal and longitudinal acceleration of superluminal charges has
been studied in [12], and radiation from superluminally rotating macroscopic light spots in [13].
As the electron plasma is magnetically confined, there is also
tachyonic synchrotron radiation inducing ripples in the radiation
densities (9) [14]. Averaged over the electron density (14), this radiation is negligible compared with the inertial emission caused by the negative mass-square [15].
, so that the transversal and longitudinal dispersion relations (7) coincide. Radiation from uniformly moving subluminal charges is generated by the Cherenkov mechanism [10,11]. The radiated tachyonic quanta can be sub- or superluminal, cf. (31).
Apart from the inertial Cherenkov effect, electromagnetic radiation by
transversal and longitudinal acceleration of superluminal charges has
been studied in [12], and radiation from superluminally rotating macroscopic light spots in [13].
As the electron plasma is magnetically confined, there is also
tachyonic synchrotron radiation inducing ripples in the radiation
densities (9) [14]. Averaged over the electron density (14), this radiation is negligible compared with the inertial emission caused by the negative mass-square [15].
We measure energy in GeV units, writing E for 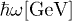 , and consider a power-law frequency variation of the tachyon mass and the tachyonic fine-structure constant,
, and consider a power-law frequency variation of the tachyon mass and the tachyonic fine-structure constant,
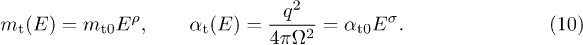
Here, we have identified the scaling function 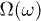 in (5) and (9) as
in (5) and (9) as 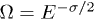 . The amplitude
. The amplitude 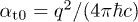 is dimensionless, being the tachyonic counterpart to the electric fine-structure constant
is dimensionless, being the tachyonic counterpart to the electric fine-structure constant 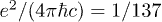 .
. 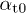 and
and 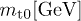 are positive amplitudes. The mass scaling exponent ρ is restricted to
are positive amplitudes. The mass scaling exponent ρ is restricted to 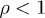 , see after (21). In the range
, see after (21). In the range 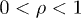 , we will find subexponential decay
, we will find subexponential decay 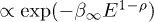 of the energy flux, cf. (26).
of the energy flux, cf. (26).
We substitute the wave numbers (7) into the spectral densities (9) and parametrize the velocity of the subluminal charge with the Lorentz factor, 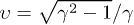 ,
,
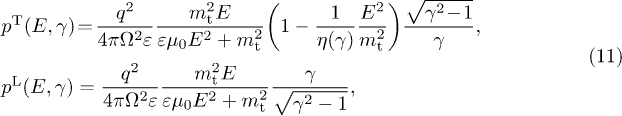
where we use the shortcut

Equation 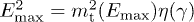 is equivalent to
is equivalent to 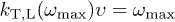 , as the dispersion relations (7) are identical for
, as the dispersion relations (7) are identical for 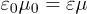 , cf. after (9), so that
, cf. after (9), so that 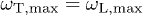 in (8) and
in (8) and 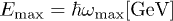 . Substituting
. Substituting 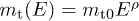 , cf. (10), we can solve for
, cf. (10), we can solve for 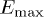 to find the highest frequency radiated by an inertial charge with Lorentz factor γ,
to find the highest frequency radiated by an inertial charge with Lorentz factor γ,
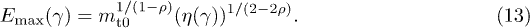
Since 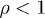 ,
, 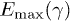 is monotonically increasing. For the classical densities (9) to be applicable,
is monotonically increasing. For the classical densities (9) to be applicable, 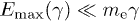 has to hold, where
has to hold, where 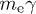 is the energy of the radiating charge.
is the energy of the radiating charge.
We average the radiation densities (11) over an electronic power-law distribution [16],
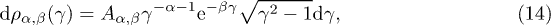
parametrized with the electronic Lorentz factor γ. The dimensionless normalization constant 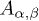 is related to the electron number
is related to the electron number 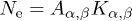 by
by
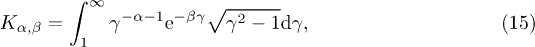
where 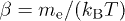 is the dimensionless temperature parameter and
is the dimensionless temperature parameter and 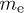 the electron mass, so that
the electron mass, so that 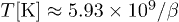 . A Maxwell-Boltzmann equilibrium distribution requires the electron index
. A Maxwell-Boltzmann equilibrium distribution requires the electron index 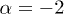 ;
; 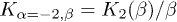 is a modified Bessel function.
is a modified Bessel function.
The spectral average of the radiation densities (11) is carried out as
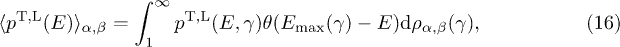
where θ is the Heaviside step function. We solve the inequality 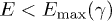 for γ, with
for γ, with 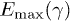 in (13):
in (13): 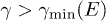 ,
,
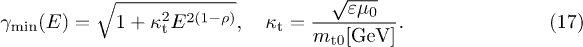
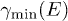 is monotonically increasing for
is monotonically increasing for 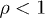 . For a frequency E to be radiated, this requires the Lorentz factor to exceed
. For a frequency E to be radiated, this requires the Lorentz factor to exceed 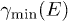 . The average (16) can thus be reduced to
. The average (16) can thus be reduced to
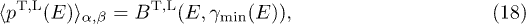
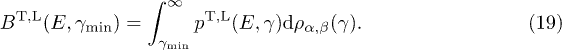
More explicitly, the transversal/longitudinal spectral functions 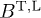 read
read
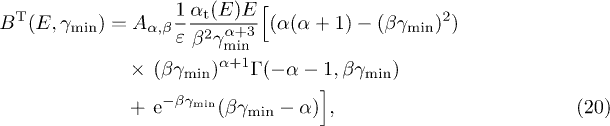
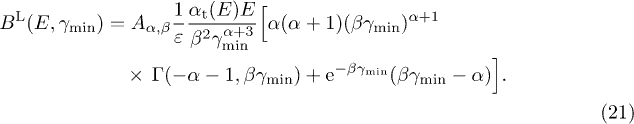
We write 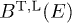 for
for 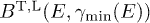 . The unpolarized radiation density is
. The unpolarized radiation density is 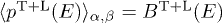 , with
, with 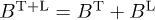 . For a thermal electron distribution,
. For a thermal electron distribution, 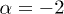 , the spectral functions simplify since
, the spectral functions simplify since 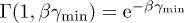 . The asymptotic limit of the incomplete gamma function is
. The asymptotic limit of the incomplete gamma function is 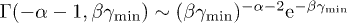 , applicable for
, applicable for 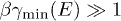 , so that the spectral functions
, so that the spectral functions 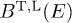 decay subexponentially
decay subexponentially 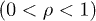 or superexponentially
or superexponentially 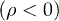 for
for 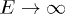 , cf. (17). The minimal Lorentz factor
, cf. (17). The minimal Lorentz factor 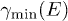 in (17) remains valid for
in (17) remains valid for 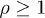 , but the limit
, but the limit 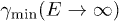 is finite, so that a genuine exponential decay factor is lacking in the
spectral functions. Therefore we restrict the mass scaling exponent to
is finite, so that a genuine exponential decay factor is lacking in the
spectral functions. Therefore we restrict the mass scaling exponent to 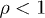 .
.
The differential energy flux 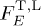 and the differential number flux
and the differential number flux 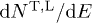 are related to the spectral functions
are related to the spectral functions 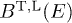 by, cf. (18),
by, cf. (18),
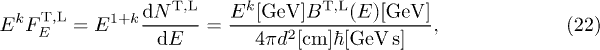
where 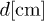 is the distance to the source, and
is the distance to the source, and 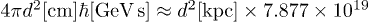 [17]. It is convenient to rescale
[17]. It is convenient to rescale 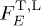 with a power Ek to make steep spectral slopes better visible; we will put k = 1. The total differential flux
with a power Ek to make steep spectral slopes better visible; we will put k = 1. The total differential flux 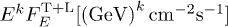 is obtained by adding the polarization components, substituting
is obtained by adding the polarization components, substituting 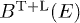 into (22). We find, by assembling (20)–(22),
into (22). We find, by assembling (20)–(22),
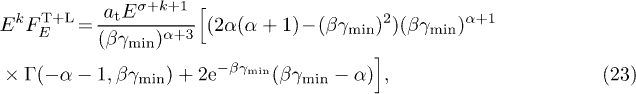
with 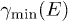 defined in (17). The combined amplitude
defined in (17). The combined amplitude
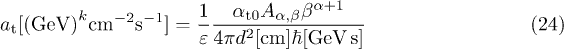
is a fitting parameter. For a thermal electron population (14) with 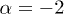 , the unpolarized flux (23) simplifies to
, the unpolarized flux (23) simplifies to
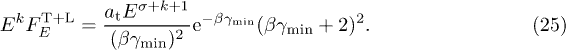
We study the high-energy limit 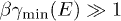 ,
, 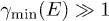 , and the intermediate regime
, and the intermediate regime 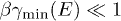 ,
, 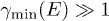 , cf. (17), of the unpolarized differential flux density
, cf. (17), of the unpolarized differential flux density 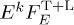 in (23). The energy range of LAT pulsar spectra [1] lies above 100 MeV. The tachyon-electron mass ratio is assumed to be small,
in (23). The energy range of LAT pulsar spectra [1] lies above 100 MeV. The tachyon-electron mass ratio is assumed to be small, 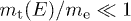 , cf. (10), otherwise we would have to quantize the Cherenkov densities (9) (see [18] for the vacuum quantum densities). Thus we can approximate
, cf. (10), otherwise we would have to quantize the Cherenkov densities (9) (see [18] for the vacuum quantum densities). Thus we can approximate 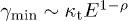 in the LAT spectral range, since
in the LAT spectral range, since  for
for 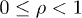 , cf. (17). The above limits correspond to
, cf. (17). The above limits correspond to 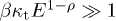 and
and 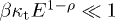 ; the latter is not to be confused with the low-frequency limit
; the latter is not to be confused with the low-frequency limit 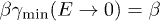 applicable in the radio band [9], where
applicable in the radio band [9], where 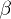 and
and 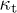 become independent fitting parameters.
become independent fitting parameters.
In the high-energy regime 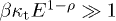 , we fit the spectral tail with
, we fit the spectral tail with
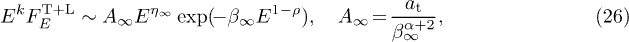

The scaling exponent ρ of the tachyon mass, cf. (10), determines the shape parameter 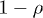 of the Weibull exponential in (26), cf. [19].
of the Weibull exponential in (26), cf. [19].
In the intermediate-energy range (at high temperature), 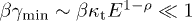 , the flux reads
, the flux reads
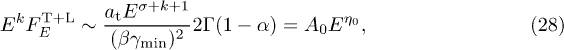
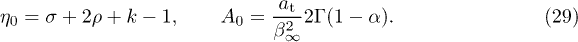
We restrict here to electron indices 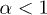 to save notation; this sufficiently covers the equilibrium index
to save notation; this sufficiently covers the equilibrium index 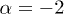 . A0 and
. A0 and  can be estimated by fitting the power-law slope (28) (linear in a
can be estimated by fitting the power-law slope (28) (linear in a  plot) to the lower end of the LAT spectrum. The amplitude and scaling relations
plot) to the lower end of the LAT spectrum. The amplitude and scaling relations
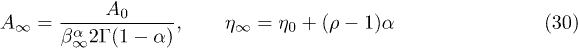
are to be substituted into the high-frequency limit (26). We determine initial guesses for A0 and 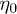 from a fit of the ascending slope with (28), insert these parameters into (30), and obtain
from a fit of the ascending slope with (28), insert these parameters into (30), and obtain 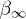 , ρ and α by fitting the spectral tail with (26). The fine-structure scaling exponent σ and the flux amplitude
, ρ and α by fitting the spectral tail with (26). The fine-structure scaling exponent σ and the flux amplitude 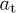 are inferred from (29). These parameters serve as initial guess in the
are inferred from (29). These parameters serve as initial guess in the 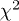 fit based on (23) or (25), where we substitute
fit based on (23) or (25), where we substitute 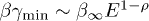 . The fitting parameters are α, σ, ρ,
. The fitting parameters are α, σ, ρ, 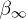 and
and 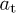 ; we will prescribe the electron index,
; we will prescribe the electron index, 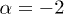 , of an electron gas in thermal equilibrium.
, of an electron gas in thermal equilibrium.
In figs. 1–3, we plot the energy flux 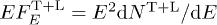 , cf. (25),
performing tachyonic Cherenkov fits to the LAT spectra of the Vela
pulsar, PSR J1709 − 4429 and Geminga. These spectra show
distinctly subexponential Weibull decay,
, cf. (25),
performing tachyonic Cherenkov fits to the LAT spectra of the Vela
pulsar, PSR J1709 − 4429 and Geminga. These spectra show
distinctly subexponential Weibull decay, 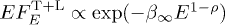 ,
, 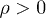 , cf. (26) and table 1. Since the tachyon mass
, cf. (26) and table 1. Since the tachyon mass 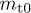 is much smaller than the electron mass and the decay exponent
is much smaller than the electron mass and the decay exponent 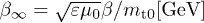 is moderate, cf. table 1, the temperature parameter β must be small, so that the thermal electron plasma is ultra-relativistic, cf. (14).
is moderate, cf. table 1, the temperature parameter β must be small, so that the thermal electron plasma is ultra-relativistic, cf. (14).
The energy dependence of the tachyon mass and the tachyonic fine-structure constant, cf. (10), can be absorbed in the permeabilities, by redefining 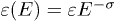 ,
, 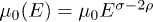 and retaining the relations
and retaining the relations 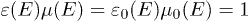 , cf. after (9). We can then put
, cf. after (9). We can then put 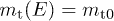 ,
, 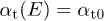 . That is, the spectral functions
. That is, the spectral functions 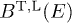 in (20) and (21) do not change if we keep
in (20) and (21) do not change if we keep 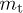 and
and 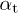 constant and use frequency-dependent permeabilities instead. The minimal Lorentz factor (17) stays invariant as well, since
constant and use frequency-dependent permeabilities instead. The minimal Lorentz factor (17) stays invariant as well, since 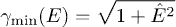 ,
, 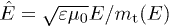 .
.
The refractive indices 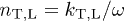 , cf. (7), are related to the transversal and longitudinal group velocities by
, cf. (7), are related to the transversal and longitudinal group velocities by 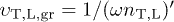 . The condition
. The condition 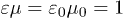 implies
implies 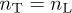 and, cf. (10),
and, cf. (10),
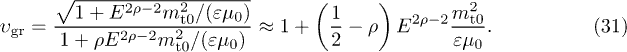
Whether this velocity is sub- or superluminal can be read off from the Weibull shape parameter of the spectral tail, cf. (26), from which the scaling exponent ρ of the tachyon mass is inferred: 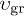 is subluminal for
is subluminal for 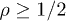 and superluminal for
and superluminal for 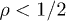 . Tachyonic γ-rays from the Vela pulsar and PSR J1709 − 4429 are thus subluminal, cf. table 1, whereas the γ-ray emission of Geminga is superluminal. The rescaled tachyonic mass amplitude
. Tachyonic γ-rays from the Vela pulsar and PSR J1709 − 4429 are thus subluminal, cf. table 1, whereas the γ-ray emission of Geminga is superluminal. The rescaled tachyonic mass amplitude 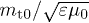 can be inferred by measuring the group velocity (31); the electron temperature is then obtained via (17), (27) and
can be inferred by measuring the group velocity (31); the electron temperature is then obtained via (17), (27) and 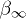 in table 1.
in table 1.
The tachyonic Cherenkov densities (9) are derived from classical Maxwell-Proca equations, cf. (1)–(7), and are independent of the mass of the radiating charge, in contrast to the quantized densities which depend on the tachyon-electron mass ratio; this will be discussed elsewhere.
↑ Close