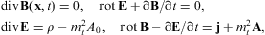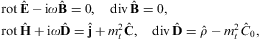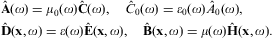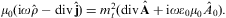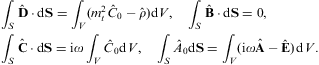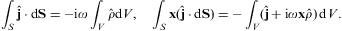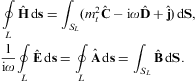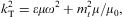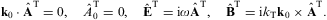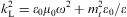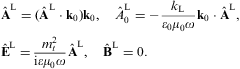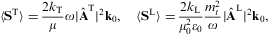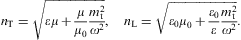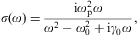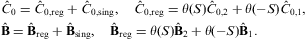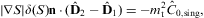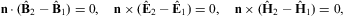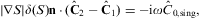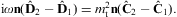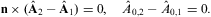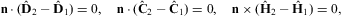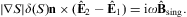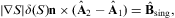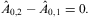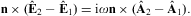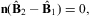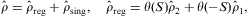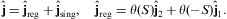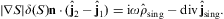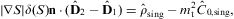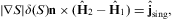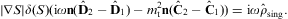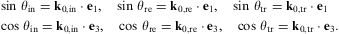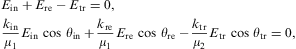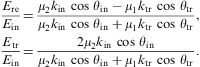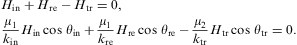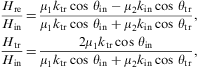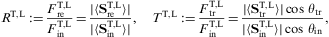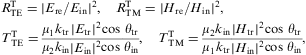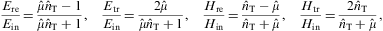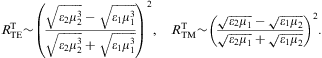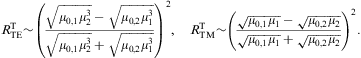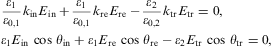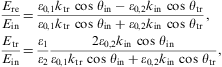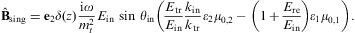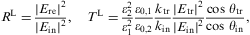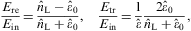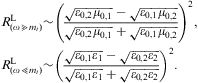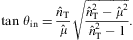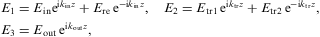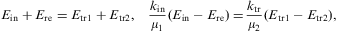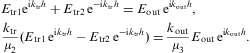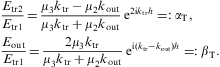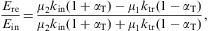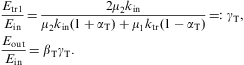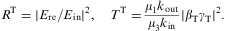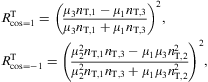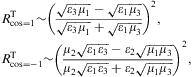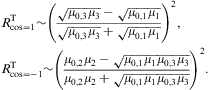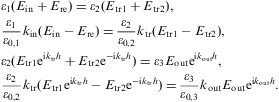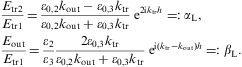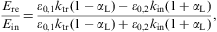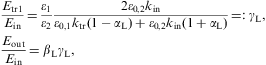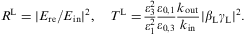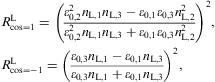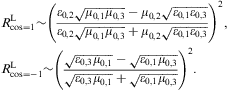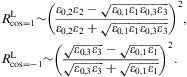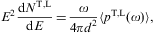Volume 404, Issues 8-11, 1 May 2009, Pages 1383-1393
Roman
Tomaschitz ,
a,
,
a,

Abstract
The propagation of superluminal waves in dispersive media is investigated, in particular the refraction at surfaces of discontinuity in layered dielectrics. The negative mass-square of the tachyonic modes is manifested in the transmission and reflection coefficients, and the polarization of the incident waves (TE, TM, or longitudinal) can be determined from the refraction angles. The conditions for total internal reflection in terms of polarization and tachyon mass are derived. Brewster angles can be used to discriminate longitudinal from transversal incidence. Superluminal transmission through dielectric boundary layers is studied, and the dependence of the intensity maxima on the transversal and longitudinal refractive indices of the layer is analyzed. Estimates of the tachyonic plasma frequency and permittivity of metals are given. The integral version of the tachyonic Maxwell equations is stated, boundary conditions at the surfaces of discontinuity are derived for transversal and longitudinal wave propagation, and singular surface fields and currents are pointed out. The spectral maps of three TeV γ-ray sources associated with supernova remnants, which have recently been obtained with imaging atmospheric Cherenkov detectors, are fitted with tachyonic cascade spectra. The transversal and longitudinal polarization components are disentangled in the spectral maps, and the thermodynamic parameters of the shock-heated ultra-relativistic electron plasma generating the tachyon flux are extracted from the cascade fits.
Keywords: Superluminal wave propagation; Tachyonic Maxwell equations; Boundary conditions for radiation modes with negative mass-square; Transversal and longitudinal refraction; Polarization of tachyonic γ-rays; Tachyonic plasma frequency; Nonthermal cascade spectra
PACS classification codes: 42.25.Bs; 42.25.Gy; 52.25.Mq; 95.30.Gv
Article Outline
- 1. Introduction
- 2. Tachyonic Maxwell equations and integral field equations in a permeable medium
- 3. Superluminal wave fields at the surface of discontinuity of dielectrics and conductors
- 3.1. Boundary conditions for transversal tachyons
- 3.2. Longitudinal modes generating singular magnetic field strengths at the interface
- 3.3. Singular boundary currents and charge densities
- 4. Tachyon refraction at plane interfaces of dispersive media
- 4.1. Refraction of superluminal TE and TM waves
- 4.2. Manifestations of the negative mass-square: longitudinal refraction, Brewster angles, and total internal reflection
- 4.3. Normal incidence: reflection and transmission of tachyons at a boundary layer
- 5. Polarization components of tachyonic cascades radiated by a shock-heated electron plasma
- 6. Conclusion
- Acknowledgements
- References
1. Introduction
We investigate the refraction of superluminal wave modes in dispersive media, at dielectric interfaces and boundary layers. The formalism is developed in analogy to electromagnetic theory [1], even though there are substantial differences due to the negative mass-square of tachyons [2], [3], [4] and [5] and the occurrence of longitudinally polarized modes [6] and [7]. The tachyon mass shows in deflection angles, transmission coefficients, and in longitudinal refraction. The superluminal radiation field is a real Proca field with negative mass-square [8]. In 3D, the wave modes can be written in terms of field strengths and inductions, suggesting a counterpart to Maxwell's equations. The tachyonic Maxwell equations explicitly depend on the scalar and vector potentials, so that the gauge invariance is broken. We derive differential and integral field equations, including the material equations in a dispersive medium relating the tachyonic field strengths and potentials to inductions via frequency-dependent permeabilities.The field equations, the polarization of superluminal modes, and the transversal and longitudinal Poynting vectors of the tachyon flux in a dispersive medium are discussed in Section 2. The transversal and longitudinal refractive indices for tachyonic wave propagation in dielectrics are introduced, and estimates of the tachyonic conductivity of metals are given. Refraction properties such as deflection and reflection angles are determined by boundary conditions on the tachyon potential, the field strengths, and inductions at the surface of discontinuity. There are two types of boundary conditions depending on the polarization of the wave fields, and singular magnetic field strengths and boundary currents can emerge. This is explained in Section 3.
In Section 4, we study superluminal refraction at a plane interface generated by a discontinuity in the permeabilities. The reflection and refraction angles depend on the polarization of the incident modes, and so do the transmission rates. The Brewster angles for transversal and longitudinal incidence are derived, as well as the conditions for total internal reflection of polarized superluminal radiation. The tachyon flux through a dielectric boundary layer is investigated, in particular the intensity peaks at normal incidence. We calculate the transmission and reflection coefficients, and discuss their frequency dependence and the effect of polarization.
In Section 5, we point out evidence for superluminal γ-rays in the spectral maps of three Galactic TeV sources obtained with the imaging air Cherenkov detectors HESS and MAGIC [9], [10] and [11]. The spectra are fitted with nonthermal tachyonic cascades generated by the shocked electron plasma of the remnants. The transversal and longitudinal polarization components of the cascades are resolved, exhibiting extended spectral plateaus in the high GeV region typical for tachyonic γ-ray emitters, followed by nonthermal power–law slopes at low TeV energies. The spectral break terminating the GeV plateau is compared to the break energies of the cosmic-ray spectrum. In Section 6, we present our conclusions.
2. Tachyonic Maxwell equations and integral field equations in a permeable medium
The tachyonic radiation field in vacuum is a real vector field
with negative mass-square, satisfying the Proca equation ![]() ,
subject to the Lorentz condition
,
subject to the Lorentz condition ![]() .
mt is the mass of the
superluminal Proca field Aμ,
and q the tachyonic charge carried by the
subluminal electron current jμ=(ρ,j).
The mass term is added with a positive sign, and the sign convention
for the metric defining the d’Alembertian ∂ν∂ν
is diag (−1,1,1,1), so that
.
mt is the mass of the
superluminal Proca field Aμ,
and q the tachyonic charge carried by the
subluminal electron current jμ=(ρ,j).
The mass term is added with a positive sign, and the sign convention
for the metric defining the d’Alembertian ∂ν∂ν
is diag (−1,1,1,1), so that ![]() is the negative mass-square of the radiation field [6] and [12]. The above
wave equation in conjunction with the Lorentz condition is equivalent
to the tachyonic Maxwell equations
is the negative mass-square of the radiation field [6] and [12]. The above
wave equation in conjunction with the Lorentz condition is equivalent
to the tachyonic Maxwell equations
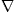 A0-∂A/∂t
and
A0-∂A/∂t
and In a permeable medium, the potentials and field strengths in
the inhomogeneous vacuum equations (2.1) are
replaced by inductions, (A0,A)→(C0,C),
(E,B)→(D,H),
defined by material equations [13] and [14]. We will
mostly consider monochromatic waves, ![]() ,
and analogously for the scalar potential, current, charge density,
field strengths, and inductions. Fourier amplitudes are denoted by a
hat. Maxwell's equations in Fourier space read
,
and analogously for the scalar potential, current, charge density,
field strengths, and inductions. Fourier amplitudes are denoted by a
hat. Maxwell's equations in Fourier space read
The inductive potentials
Current conservation,
The sign conventions for the coupling of an electron to the
Proca field are L=-m/γ+q(A0+A·v)
and md(γv)/dt=q(E+v×B),
where γ=(1-υ2)-1/2
is the electronic Lorentz factor and q the
tachyonic charge carried by the electron, cf. after Eq. (2.14). The
primary fields rather than the inductions define the Lorentz force. The
potentials are unambiguously determined by the field strengths and the
dielectric and magnetic permeabilities. We define polarizations ![]() ,
,
![]() ,
and
,
and ![]() ,
relating the inductions and field strengths additively as
,
relating the inductions and field strengths additively as ![]() and
and ![]() ,
and analogously the potentials
,
and analogously the potentials ![]() and
and ![]() .
Accordingly,
.
Accordingly, ![]() and
and ![]() ,
with electric susceptibilities κ=ε-1
and κ0=ε0-1.
Analogously,
,
with electric susceptibilities κ=ε-1
and κ0=ε0-1.
Analogously, ![]() and
and ![]() ,
with magnetic susceptibilities χ=μ-1
and χ0=μ0-1.
The permeabilities ε0 and μ0
define the inductive potentials in Eq. (2.3), and are
not to be confused with vacuum permeabilities; we use the
Heaviside–Lorentz system, so that ε=ε0=1
and μ=μ0=1
in vacuum.
,
with magnetic susceptibilities χ=μ-1
and χ0=μ0-1.
The permeabilities ε0 and μ0
define the inductive potentials in Eq. (2.3), and are
not to be confused with vacuum permeabilities; we use the
Heaviside–Lorentz system, so that ε=ε0=1
and μ=μ0=1
in vacuum.
Applying the Gauss theorem to the divergence equations in Eq. (2.2), as well
as to the Lorentz condition and the potential definition of ![]() ,
cf. after Eq. (2.3), we find
the integral field equations
,
cf. after Eq. (2.3), we find
the integral field equations
Applying the Stokes theorem to the rotor equations in Eq. (2.2) and the potential definition of
Here, dS=ndS is the surface element of an oriented open surface SL bounded by the closed loop L, and ds=n×nL ds is the oriented tangent element of the loop. nL is the unit vector tangent to the surface and orthogonal to the loop, pointing to the exterior. n is the unit normal of the surface at the loop, with the same orientation as the surface element dS.
To find the transversal and longitudinal dispersion relations,
we use a plane–wave ansatz in the Maxwell equations (2.2) with
vanishing charge and current densities: ![]() ,
and analogously for the scalar potential and the field strengths. Here,
k=k(ω)k0,
where k is the wave number to be determined from
the field equations, and k0
is a constant unit vector. k(ω)
as well as k0 can
be complex. The transversality condition is
,
and analogously for the scalar potential and the field strengths. Here,
k=k(ω)k0,
where k is the wave number to be determined from
the field equations, and k0
is a constant unit vector. k(ω)
as well as k0 can
be complex. The transversality condition is ![]() ,
and the set of transversal modes is
,
and the set of transversal modes is ![]() ,
with amplitude
,
with amplitude ![]() ,
and similarly for the field strengths and the scalar potential. The
dispersion relation determining the transversal wave number is
,
and similarly for the field strengths and the scalar potential. The
dispersion relation determining the transversal wave number is
If the product
so that
The amplitudes AT,L(k) only need to satisfy the transversality/longitudinality condition, that is, the first equation in Eqs. (2.9) and (2.11), respectively.
The time-averaged tachyonic energy flux carried by homogeneous
modes (with real wave vector k0)
in a dispersive and non-absorptive medium is
The transversal and longitudinal phase velocities read ![]() ,
and the tachyonic group velocities are
,
and the tachyonic group velocities are ![]() ,
so that
,
so that ![]() and
and ![]() .
In the case of vacuum permeabilities, ε(0)=μ(0)=1,
the transversal and longitudinal velocities coincide, and we find ω=mtγt,
where
.
In the case of vacuum permeabilities, ε(0)=μ(0)=1,
the transversal and longitudinal velocities coincide, and we find ω=mtγt,
where ![]() denotes the tachyonic Lorentz factor and υgr>1
is the superluminal group velocity. The refractive index nT,L=kT,L/ω,
defined as dimensionless inverse phase velocity, differs for
transversal and longitudinal modes:
denotes the tachyonic Lorentz factor and υgr>1
is the superluminal group velocity. The refractive index nT,L=kT,L/ω,
defined as dimensionless inverse phase velocity, differs for
transversal and longitudinal modes:
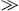 mt
(with
mt
(with 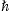 =c=1),
we can approximate
=c=1),
we can approximate 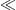 mt,
the refractive indices are frequency dependent even if the
permeabilities stay constant,
mt,
the refractive indices are frequency dependent even if the
permeabilities stay constant, To estimate the dielectric permeability for tachyonic wave
propagation, we start with a monochromatic superluminal mode, ![]() ,
in a dispersive and possibly dissipative medium. This mode generates
the current
,
in a dispersive and possibly dissipative medium. This mode generates
the current ![]() ,
,
![]() ,
where σ(ω) is the tachyonic
conductivity of the medium, cf. Eq. (2.14). The
charge distribution
,
where σ(ω) is the tachyonic
conductivity of the medium, cf. Eq. (2.14). The
charge distribution ![]() is found by means of current conservation, cf. after Eq. (2.4). We
substitute this current into the field equations (2.2) with
vacuum permeabilities ε(0)=μ(0)=1,
and absorb current and charge density by introducing the permittivity εσ(ω)=1+iσ(ω)/ω.
In this way, we can write the inhomogeneous field equations (2.2) as
is found by means of current conservation, cf. after Eq. (2.4). We
substitute this current into the field equations (2.2) with
vacuum permeabilities ε(0)=μ(0)=1,
and absorb current and charge density by introducing the permittivity εσ(ω)=1+iσ(ω)/ω.
In this way, we can write the inhomogeneous field equations (2.2) as ![]() and
and ![]() ;
the homogeneous Maxwell equations remain unchanged. The polarization
vector is
;
the homogeneous Maxwell equations remain unchanged. The polarization
vector is ![]() ,
cf. after Eq. (2.4), and the
London equation
,
cf. after Eq. (2.4), and the
London equation ![]() applies. The dispersion relations for the transversal and longitudinal
modes read as in Eqs. (2.8) and (2.10), with ε
replaced by εσ
and ε0=μ(0)=1.
applies. The dispersion relations for the transversal and longitudinal
modes read as in Eqs. (2.8) and (2.10), with ε
replaced by εσ
and ε0=μ(0)=1.
We consider a tachyonic conductivity
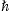 c)≈1/137
and αq=q2/(4π
c)≈1/137
and αq=q2/(4π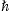 c)≈1.0×10-13.
The tachyon–electron mass ratio is mt/m≈1/238;
αq and mt
are estimated from hydrogenic Lamb shifts [6]. We may thus
conclude that the tachyonic conductivity
c)≈1.0×10-13.
The tachyon–electron mass ratio is mt/m≈1/238;
αq and mt
are estimated from hydrogenic Lamb shifts [6]. We may thus
conclude that the tachyonic conductivity To demonstrate this, we consider a free electron gas, ω0=γ0=0,
so that the tachyonic conductivity (2.14)
simplifies to ![]() ,
and the induced permittivity is
,
and the induced permittivity is ![]() .
We may write the electromagnetic plasma frequency as
.
We may write the electromagnetic plasma frequency as ![]() ,
where
,
where 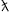 e is the reduced
electronic Compton wavelength, αe
the electric fine structure constant, and ne
the electron density as above. We thus find
e is the reduced
electronic Compton wavelength, αe
the electric fine structure constant, and ne
the electron density as above. We thus find ![]() ,
and the tachyonic counterpart ωp≈3.74×10-6ωp,em.
Metallic electron densities of 1022−1023 cm−3
result in a tachyonic plasma frequency ωp
in the 10−5 eV range. Thus, even though
the tachyonic conductivity is much smaller than the electromagnetic one
at the same frequency, the tachyonic permittivity εσ(ω)
becomes noticeably different from 1 for frequencies comparable to ωp.
Finally, small frequencies of the order of 10−5 eV
do not imply large wavelengths. The tachyonic wavelength is λT,L=2π/kT,L,
with wave numbers defined in Eqs. (2.8) and (2.10). The
maximal transversal/longitudinal wavelength in the medium is thus
,
and the tachyonic counterpart ωp≈3.74×10-6ωp,em.
Metallic electron densities of 1022−1023 cm−3
result in a tachyonic plasma frequency ωp
in the 10−5 eV range. Thus, even though
the tachyonic conductivity is much smaller than the electromagnetic one
at the same frequency, the tachyonic permittivity εσ(ω)
becomes noticeably different from 1 for frequencies comparable to ωp.
Finally, small frequencies of the order of 10−5 eV
do not imply large wavelengths. The tachyonic wavelength is λT,L=2π/kT,L,
with wave numbers defined in Eqs. (2.8) and (2.10). The
maximal transversal/longitudinal wavelength in the medium is thus ![]() and
and ![]() ,
attained in the zero frequency limit, where the permeabilities are of
order one and
,
attained in the zero frequency limit, where the permeabilities are of
order one and ![]() is the tachyonic Compton wavelength.
is the tachyonic Compton wavelength.
3. Superluminal wave fields at the surface of discontinuity of dielectrics and conductors
To study tachyon refraction at the interface of two media with
different permeabilities, we have to specify the boundary conditions.
To this end, we split the wave fields into regular and singular parts,
writing the scalar induction and the magnetic field strength as
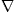 S/|
S/|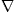 S|, thus points into
the interior of medium 2. The singular part of the field, if any, is a
distribution supported on the boundary surface S=0,
typically containing a Dirac function δ(S)
as factor. In contrast to the regular components in Eq. (3.1), the
singular field strengths and inductions do not show in the material
equations (2.3). In
Sections 3.1 and 3.2, we assume
vanishing charge and current densities in the field equations, as well
as the absence of a singular surface current at the interface. In Section 3.3, we
consider inhomogeneous boundary conditions consistent with currents.
S|, thus points into
the interior of medium 2. The singular part of the field, if any, is a
distribution supported on the boundary surface S=0,
typically containing a Dirac function δ(S)
as factor. In contrast to the regular components in Eq. (3.1), the
singular field strengths and inductions do not show in the material
equations (2.3). In
Sections 3.1 and 3.2, we assume
vanishing charge and current densities in the field equations, as well
as the absence of a singular surface current at the interface. In Section 3.3, we
consider inhomogeneous boundary conditions consistent with currents.
3.1. Boundary conditions for transversal tachyons
We start by substituting ansatz (3.1) into the
field equations (2.2) (with zero
current and charge density) and the Lorentz condition, and assume that
the fields subjected to rotors and divergences have no singular part.
That is, we try to solve under the condition that ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
and
,
and ![]() are regular at the interface, obtaining five relations to be satisfied
at the boundary S=0,
are regular at the interface, obtaining five relations to be satisfied
at the boundary S=0,
where Eqs. (3.2) and (3.4) can be combined to give
Assuming the potentials
All fields are regular at the boundary surface, with exception of
3.2. Longitudinal modes generating singular magnetic field strengths at the interface
We proceed analogously to the transversal case, but now
assuming all fields to be regular at the boundary except for the
magnetic field ![]() .
On substituting ansatz (3.1) into the
field equations (2.3) and (2.4) and the
Lorentz condition, cf. after Eq. (2.4), we find
.
On substituting ansatz (3.1) into the
field equations (2.3) and (2.4) and the
Lorentz condition, cf. after Eq. (2.4), we find
The potential representations of
By combining Eqs. (3.8) and (3.9), we obtain
Finally, the divergence equation,
where we used (3.9). Eqs. (3.7), (3.10), (3.11) and (3.12) constitute the boundary conditions for longitudinal modes. The regular longitudinal
The transversal and longitudinal boundary conditions derived in Sections 3.1 and 3.2 apply at the interface of two media with different permeabilities discontinuous at the interface. They unambiguously determine the refractive properties of tachyons, such as deflection and reflection angles, and assure transmission and reflection ratios consistent with energy conservation in non-absorptive media, cf. Section 4.
3.3. Singular boundary currents and charge densities
In the case of non-vanishing charge and current densities in
field equations (2.2), the
transversal and longitudinal boundary conditions derived in Sections 3.1 and 3.2 become
inhomogeneous due to singular surface currents. As in (3.1), we split
current and charge density into a regular and singular part,
The singular surface charge and current,
Three of the transversal boundary conditions in Section 3.1 have to be modified in the presence of currents. Condition (3.2) is replaced by
the third condition in Eq. (3.3) reads
and condition (3.5) becomes inhomogeneous as well:
As for the longitudinal boundary conditions in Section 3.2, there are two changes. The first condition in Eq. (3.7) is replaced by Eq. (3.15) with
4. Tachyon refraction at plane interfaces of dispersive media
We take the z=0 plane as the interface S
separating medium 2 in the upper half-space z>0
from medium 1 in the lower half-space. The media are defined by
frequency-dependent permeabilities (ε0,1,ε1,μ0,1,μ1)
and (ε0,2,ε2,μ0,2,μ2),
respectively, cf. Eq. (2.3) and after
Eq. (3.1). We
consider a tachyonic plane wave, cf. after Eq. (2.7), incident
from the lower half-space upon the interface, the e1,2
plane. The wave number kin
of this incoming transversal or longitudinal wave is defined by
dispersion relation (2.8) or (2.10), with
permeabilities carrying subscript 1. Part of the wave is reflected back
into medium 1, and the wave number kre
of the reflected wave coincides with kin.
The wave number ktr of the
wave transmitted into the upper half-space is determined by the
permeabilities of medium 2. The wave vectors of the respective modes
are denoted by kin=kink0,in,
kre=krek0,re,
and ktr=ktrk0,tr,
where the zero subscript indicates unit vectors. We assume the incoming
plane wave to be homogeneous, so that k0,in
is a real unit vector; the wave numbers kin,tr
can be complex. Since k0,in
is real, the unit wave vector k0,re
of the reflected wave is real too, as shown below. The transmitted wave
is in general inhomogeneous if the wave number in medium 1 or 2 is
complex, so that k0,tr
is a complex unit vector, ![]() .
We adopt the convention Re(kin,tr)>0,
since wave numbers are only defined as squares by the dispersion
relations. If medium 1 in the lower half-space has real permeabilities,
the vacuum for instance, then the incident wave number kin
is real.
.
We adopt the convention Re(kin,tr)>0,
since wave numbers are only defined as squares by the dispersion
relations. If medium 1 in the lower half-space has real permeabilities,
the vacuum for instance, then the incident wave number kin
is real.
We choose the incoming real unit wave vector k0,in
in the e1,3 plane.
(The ei
are coordinate unit vectors.) The normal vector of the interface is e3,
pointing into medium 2. A convenient angular parametrization of the
wave vectors is
The refractive indices of medium 1 and 2 are denoted by n1,2=kin,tr/ω,
cf. Eq. (2.13), and
their ratio by ![]() .
This applies to transversal as well as longitudinal indices, e.g.,
.
This applies to transversal as well as longitudinal indices, e.g., ![]() .
The transversal/longitudinal refraction law can thus be written as
.
The transversal/longitudinal refraction law can thus be written as ![]() .
In the high-frequency regime ω
.
In the high-frequency regime ω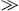 mt,
the transversal refractive index ratio simplifies to
mt,
the transversal refractive index ratio simplifies to ![]() ,
and the longitudinal one to
,
and the longitudinal one to ![]() ,
cf. after Eq. (2.13). In the
low-frequency limit, ω
,
cf. after Eq. (2.13). In the
low-frequency limit, ω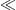 mt,
the refraction angle θtr is
determined by
mt,
the refraction angle θtr is
determined by ![]() or
or ![]() .
If we consider dielectrics with μ(0)=ε0=1,
the longitudinal refractive index ratio
.
If we consider dielectrics with μ(0)=ε0=1,
the longitudinal refractive index ratio ![]() at low frequencies is just the inverse of
at low frequencies is just the inverse of ![]() at high frequency. The refraction law can thus be used to discriminate
between transversal and longitudinal polarization.
at high frequency. The refraction law can thus be used to discriminate
between transversal and longitudinal polarization.
4.1. Refraction of superluminal TE and TM waves
We first consider tachyonic TE waves, so that the incoming
mode ![]() is linearly polarized, with amplitude orthogonal to the plane of
incidence generated by the normal vector e3
of the boundary and the wave vector k0,in
in the e1,3 plane.
Thus,
is linearly polarized, with amplitude orthogonal to the plane of
incidence generated by the normal vector e3
of the boundary and the wave vector k0,in
in the e1,3 plane.
Thus, ![]() ,
cf. Eq. (2.9). The
boundary conditions stated in Section 3.1 are
satisfied by the reflected and transmitted waves, which are likewise
polarized in the e2
direction, so that the respective modes are Eree2eikre·x
and Etre2eiktr·x.
The wave numbers of the incident and reflected waves are defined by the
transversal dispersion relation (2.8) of medium
1 with permeabilities (ε0,1,ε1,μ0,1,μ1),
cf. Eq. (2.3). The wave
number of the transmitted wave is calculated with the permeabilities (ε0,2,ε2,μ0,2,μ2)
of medium 2 in the upper half-space. The boundary conditions (3.3), (3.5) and (3.6) give, if
combined with Snell's law as stated above, two independent relations
for the three amplitudes:
,
cf. Eq. (2.9). The
boundary conditions stated in Section 3.1 are
satisfied by the reflected and transmitted waves, which are likewise
polarized in the e2
direction, so that the respective modes are Eree2eikre·x
and Etre2eiktr·x.
The wave numbers of the incident and reflected waves are defined by the
transversal dispersion relation (2.8) of medium
1 with permeabilities (ε0,1,ε1,μ0,1,μ1),
cf. Eq. (2.3). The wave
number of the transmitted wave is calculated with the permeabilities (ε0,2,ε2,μ0,2,μ2)
of medium 2 in the upper half-space. The boundary conditions (3.3), (3.5) and (3.6) give, if
combined with Snell's law as stated above, two independent relations
for the three amplitudes:
Using Snell's law, we parametrize by the incidence angle, substituting
We turn to superluminal TM waves, where the electric field is
linearly polarized parallel to the plane of incidence. It is convenient
to write the boundary conditions in terms of the magnetic field, by way
of ![]() ,
where
,
where ![]() is orthogonal to the plane of incidence, cf. Eq. (2.9).
Accordingly,
is orthogonal to the plane of incidence, cf. Eq. (2.9).
Accordingly, ![]() ,
and analogously for the reflected and transmitted modes. The boundary
conditions for transversal modes again give two independent relations
among the three amplitudes,
,
and analogously for the reflected and transmitted modes. The boundary
conditions for transversal modes again give two independent relations
among the three amplitudes,
which differ from the TE ratios just by an interchange of μ1ktr and μ2kin, and we substitute
The energy flux (i.e., the incident, reflected, or transmitted
energy per unit time and unit surface area) carried by a superluminal
mode with real unit wave vector k0
is FT,L:=|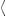 ST,L
ST,L ||k0·n|.
The transversal and longitudinal flux vectors
||k0·n|.
The transversal and longitudinal flux vectors  ST,L
ST,L are defined in Eq. (2.12), with the
respective incident, reflected, or transmitted wave substituted. As for
the transmitted wave, we assume the two media to be non-dissipative, so
that k0,tr
is real. The superscripts T and L denote transversal and longitudinal
waves, the latter are studied in Section 4.2. The
transversal and longitudinal reflection and transmission coefficients
are defined by the flux ratios
are defined in Eq. (2.12), with the
respective incident, reflected, or transmitted wave substituted. As for
the transmitted wave, we assume the two media to be non-dissipative, so
that k0,tr
is real. The superscripts T and L denote transversal and longitudinal
waves, the latter are studied in Section 4.2. The
transversal and longitudinal reflection and transmission coefficients
are defined by the flux ratios
with the amplitude ratios (4.3) and (4.5) substituted. It is easy to check that energy is conserved, which suggests that we have got the boundary conditions in Section 3.1 right.
At normal incidence, θin=θtr=0,
θre=π,
the amplitude ratios (4.3) and (4.5) reduce to
 mt,
we approximate
mt,
we approximate At low frequency ω
 mt,
we substitute
mt,
we substitute In this limit, the reflected fraction of the transversal tachyon flux is determined by the magnetic permeabilities only. Transversal refraction will further be discussed after Eq. (4.16), together with the longitudinal reflection coefficients derived in Section 4.2.
4.2. Manifestations of the negative mass-square: longitudinal refraction, Brewster angles, and total internal reflection
We start with a longitudinal incident mode, ![]() ,
and use analogous notation for the reflected and transmitted fields.
All wave vectors lie in the e1,3
plane. The permeabilities of media 1 and 2 are labeled as indicated
before Eq. (4.2). The
boundary conditions (3.7), (3.10), (3.11) and (3.12) give two
independent relations for the amplitudes,
,
and use analogous notation for the reflected and transmitted fields.
All wave vectors lie in the e1,3
plane. The permeabilities of media 1 and 2 are labeled as indicated
before Eq. (4.2). The
boundary conditions (3.7), (3.10), (3.11) and (3.12) give two
independent relations for the amplitudes,
with
The longitudinal reflection and transmission coefficients defined in Eqs. (2.12) and (4.6) are
where we substitute the ratios (4.12). The transmission coefficient applies for real permeabilities, energy being conserved in non-absorptive media, RL+TL=1.
At normal incidence, θin=θtr=0,
the ratios (4.12) simplify,
 mt,
we find
mt,
we find  mt
the refractive index becomes
mt
the refractive index becomes If we consider vacuum permeabilities in medium 1, ε(0),1=μ(0),1=1, and a dielectric permeability ε2 different from one in medium 2 (with ε0,2=μ(0),2=1), we find
 mt,
with different ε2(ω),
cf. Eq. (4.9). The
transversal reflection coefficients Eq. (4.10) valid for
ω
mt,
with different ε2(ω),
cf. Eq. (4.9). The
transversal reflection coefficients Eq. (4.10) valid for
ω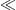 mt
vanish, as the indicated leading order of the frequency expansion is
independent of ε2.
mt
vanish, as the indicated leading order of the frequency expansion is
independent of ε2.
We consider two other special cases. First, the case where the
refracted wave vector is orthogonal to the reflected wave, θre-θtr=π/2,
so that θtr+θin=π/2,
and thus ![]() and
and ![]() .
This Brewster incidence angle,
.
This Brewster incidence angle, ![]() ,
follows from the refraction law stated after Eq. (4.1);
,
follows from the refraction law stated after Eq. (4.1); ![]() denotes the transversal or longitudinal refractive index ratio, cf.
after Eqs. (4.8) and (4.15). The
refractive indices are assumed to be real in both media. As for TM
waves, we find Hre=0
in Eq. (4.5), provided
that the magnetic permeabilities μ1
and μ2 of the two media
coincide. Similarly for longitudinally polarized waves, Ere=0
in Eq. (4.12), provided
that ε0,1=ε0,2.
At this incidence angle, the energy of a tachyonic TM wave or a
longitudinal wave is fully transmitted. If the incident transversal
wave is elliptically polarized (being a complex linear combination of
TE and TM waves), the reflected wave is a TE wave linearly polarized
orthogonal to the plane of incidence. If we do not require μ1=μ2,
and define the incidence angle by Hre=0,
we find
denotes the transversal or longitudinal refractive index ratio, cf.
after Eqs. (4.8) and (4.15). The
refractive indices are assumed to be real in both media. As for TM
waves, we find Hre=0
in Eq. (4.5), provided
that the magnetic permeabilities μ1
and μ2 of the two media
coincide. Similarly for longitudinally polarized waves, Ere=0
in Eq. (4.12), provided
that ε0,1=ε0,2.
At this incidence angle, the energy of a tachyonic TM wave or a
longitudinal wave is fully transmitted. If the incident transversal
wave is elliptically polarized (being a complex linear combination of
TE and TM waves), the reflected wave is a TE wave linearly polarized
orthogonal to the plane of incidence. If we do not require μ1=μ2,
and define the incidence angle by Hre=0,
we find
The second special case is total internal reflection, which
requires real wave numbers and incidence angles satisfying ![]() ,
so that
,
so that ![]() defined after Eq. (4.3) is zero or
imaginary with
defined after Eq. (4.3) is zero or
imaginary with ![]() to ensure damping. (More generally, the damping condition for a
transmitted wave in medium 2 is
to ensure damping. (More generally, the damping condition for a
transmitted wave in medium 2 is ![]() .)
Thus k0,tr is a
complex unit vector, even though the permeabilities in both media are
real; its e1
component
.)
Thus k0,tr is a
complex unit vector, even though the permeabilities in both media are
real; its e1
component ![]() is found via Snell's law, cf. after Eq. (4.1). The
reflection coefficients RT,L
in Eqs. (4.7) and (4.14) are equal
to 1, so that the incident flux is totally reflected. The refracted
wave in medium 2 is exponentially damped along the z
axis, and no energy is transmitted. Internal reflection can only occur
if
is found via Snell's law, cf. after Eq. (4.1). The
reflection coefficients RT,L
in Eqs. (4.7) and (4.14) are equal
to 1, so that the incident flux is totally reflected. The refracted
wave in medium 2 is exponentially damped along the z
axis, and no energy is transmitted. Internal reflection can only occur
if ![]() ,
that is, medium 1 must be optically thicker than medium 2 for
transversal or longitudinal modes. A third special case, normal
incidence on a boundary layer of finite thickness separating two
dielectric media, is discussed in the next subsection.
,
that is, medium 1 must be optically thicker than medium 2 for
transversal or longitudinal modes. A third special case, normal
incidence on a boundary layer of finite thickness separating two
dielectric media, is discussed in the next subsection.
4.3. Normal incidence: reflection and transmission of tachyons at a boundary layer
We consider three dispersive media separated by parallel
boundary planes z=0 and z=h.
Medium 1 lies in the lower half-space, medium 2 is a layer of thickness
h located in 0<z<h,
and medium 3 fills the half-space z>h.
The respective permeabilities and refractive indices are denoted by
subscripts, ε1,2,3,
etc., cf. after Eq. (3.1). The layer
is hit by a tachyonic plane wave propagating in the lower half-space
orthogonally incident upon the z=0 plane. To
satisfy the boundary conditions at the two interfaces, we start with
the ansatz
4.3.1. Transversally polarized superluminal modes
The boundary conditions for transversal tachyons read, cf.
Sections 3.1 and 4.1,
The third and fourth of these equations lead to the amplitude ratios
On substituting αT into the first and second equations in Eq. (4.19), we find
Reflection and transmission coefficients are defined as in Eqs. (4.6) and (4.7),
As for the transmission coefficient, we assume real permeabilities and wave numbers in media 1 and 3, so that damping can only occur in the boundary layer, that is medium 2. If all three media are dielectrics, energy conservation applies, RT+TT=1. In this case, the coefficients are periodic in h, the thickness of the boundary layer, and the extrema of RT and TT are determined by sin(2hktr(ω))=0, the variation being with respect to the layer thickness, ∂RT/∂h=0. Thus the intensity minima and maxima occur at frequencies where the transversal wave number ktr=ωnT,2 is an integer multiple of π/(2h); nT,2(ω) is the transversal refractive index (2.13) of the layer. We find, for cos(2hktr)=±1,
where μi denotes the magnetic permeability and nT,i the transversal refractive index of the respective medium, cf. after Eq. (2.13). In the high-frequency limit ω
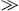 mt,
we substitute
mt,
we substitute and in the low-frequency band ω
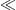 mt,
we use
mt,
we use The meaning of these extremal transversal reflection coefficients and their longitudinal counterpart is discussed after Eq. (4.32).
4.3.2. Longitudinal reflection and transmission coefficients
We proceed as in the previous case of transversal normal
incidence, starting with the longitudinal boundary conditions, cf.
Sections 3.2 and 4.2,
We substitute αL into the first and second equations in Eq. (4.26),
to find the longitudinal reflection and transmission coefficients, cf. Eq. (4.14),
If all permeabilities are real, energy is conserved, RL+TL=1, and these coefficients are periodic in the layer thickness h. The intensity extrema of RL and TL are defined by the longitudinal wave number ktr=ωnL,2(ω) in the layer, cf. Eqs. (2.10) and (2.13), occurring at frequencies solving cos(2hktr(ω))=±1, analogously to Eq. (4.23):
where nL,i is the longitudinal refractive index of the respective medium. At high frequencies, ω
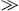 mt,
we substitute
mt,
we substitute In the low-frequency regime, we approximate
For example, we may set all permeabilities equal to one apart from the permittivity ε2 of the layer. At high frequency, the longitudinal flux is almost totally transmitted since the leading order of the reflection coefficient vanishes,
 mt.
More generally, there is a symmetry in the reflection coefficients (4.23) and (4.30) with
regard to the interchange ε0↔μ,
ε↔μ0,
which is apparent in the asymptotic limits (4.24) and (4.31) as well
as Eqs. (4.25) and (4.32). However,
the extremal frequencies defined by the zeros of sin(2hktr(ω))
differ for transversal and longitudinal modes, unless the wave numbers (2.8) and (2.10) coincide
in the layer.
mt.
More generally, there is a symmetry in the reflection coefficients (4.23) and (4.30) with
regard to the interchange ε0↔μ,
ε↔μ0,
which is apparent in the asymptotic limits (4.24) and (4.31) as well
as Eqs. (4.25) and (4.32). However,
the extremal frequencies defined by the zeros of sin(2hktr(ω))
differ for transversal and longitudinal modes, unless the wave numbers (2.8) and (2.10) coincide
in the layer.
5. Polarization components of tachyonic cascades radiated by a shock-heated electron plasma
Fig. 1, Fig. 2 and Fig. 3 depict
tachyonic cascade spectra of the TeV γ-ray sources HESS J1837−069, HESS
J1834−087, and HESS J1813−178. The cascades are plots of the E2-rescaled
flux densities,
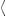 pT,L(ω=E/
pT,L(ω=E/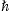 )
) the transversal/longitudinal tachyonic spectral density averaged over a
nonthermal electronic power-law distribution,
the transversal/longitudinal tachyonic spectral density averaged over a
nonthermal electronic power-law distribution,  γ<∞,
γ1
γ<∞,
γ1 1,
and the exponential cutoff is related to the electron temperature by β=mc2/(kT).
A thermal Maxwell–Boltzmann distribution corresponds to α=−2
and γ1=1. The least-squares
fit is performed with the unpolarized flux density dNT+L=dNT+dNL,
and then split into transversal and longitudinal radiation components.
The details of the spectral fitting have been explained in Ref. [22]. The
parameters of the electron distributions dρα,β
generating the tachyonic cascades are listed in Table 1. The
cutoff parameter β in the Boltzmann factor could
not be extracted from the presently available flux points, in contrast
to the power–law index α and the lower edge γ1
of Lorentz factors. The power–law slope ultimately terminates in
exponential decay, cf. the spectral map of HESS J1825−137 in Fig. 5 of
Ref. [7]. As for the
spectral fits in Fig. 1, Fig. 2 and Fig. 3, there is
no downward bend yet in the presently accessible TeV range.
1,
and the exponential cutoff is related to the electron temperature by β=mc2/(kT).
A thermal Maxwell–Boltzmann distribution corresponds to α=−2
and γ1=1. The least-squares
fit is performed with the unpolarized flux density dNT+L=dNT+dNL,
and then split into transversal and longitudinal radiation components.
The details of the spectral fitting have been explained in Ref. [22]. The
parameters of the electron distributions dρα,β
generating the tachyonic cascades are listed in Table 1. The
cutoff parameter β in the Boltzmann factor could
not be extracted from the presently available flux points, in contrast
to the power–law index α and the lower edge γ1
of Lorentz factors. The power–law slope ultimately terminates in
exponential decay, cf. the spectral map of HESS J1825−137 in Fig. 5 of
Ref. [7]. As for the
spectral fits in Fig. 1, Fig. 2 and Fig. 3, there is
no downward bend yet in the presently accessible TeV range.
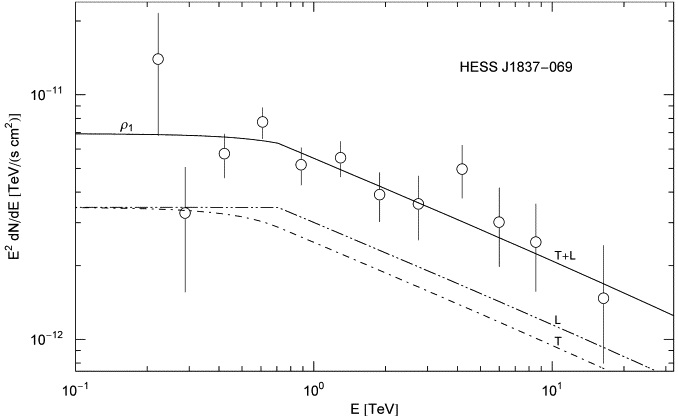
Fig. 1. Spectral map of the TeV γ-ray
source HESS J1837−069 associated with the pulsar wind nebula AX
J1838.0−0655. Flux points from Ref. [9]. The solid
line depicts the unpolarized differential tachyon flux dNT+L/dE
rescaled with E2 tachyon
flux dNT+L/dE
rescaled with E2, cf. (5.1).
The transversal (dot-dashed) and longitudinal (double-dot-dashed) flux
densities dNT,L/dE
add up to the total unpolarized flux cascade ρ1=T+L
generated by a nonthermal electron population. The cascade admits a
power–law slope ∝E1-α
with electron index α≈1.4. A spectral break at ![]() is visible as edge in the longitudinal component, where
is visible as edge in the longitudinal component, where ![]() is the tachyon mass [6] and [18]. The
least-squares fit is based on the unpolarized tachyon flux T+L, cf. Table 1.
is the tachyon mass [6] and [18]. The
least-squares fit is based on the unpolarized tachyon flux T+L, cf. Table 1.
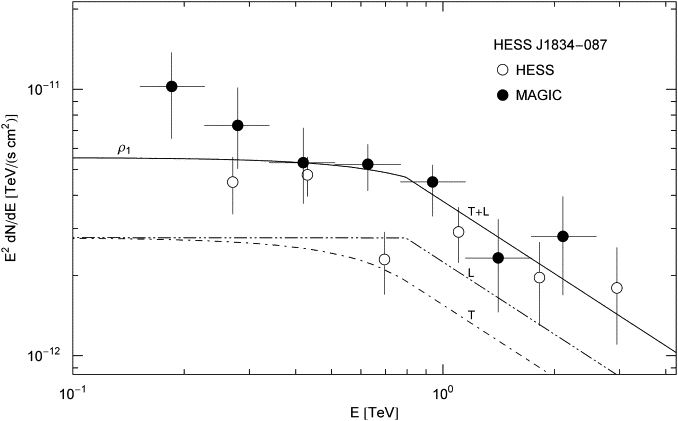
Fig. 2. Spectral map of the extended TeV source HESS J1834−087 in supernova remnant W41. HESS data points from Ref. [9], MAGIC points from Ref. [10]. Notation as in Fig. 1. The parameters of the shock-heated electron plasma are listed in Table 1. The spectral break in the longitudinal flux component (L) of the cascade occurs at 0.80 TeV. The distance estimate of this source is 4 kpc, and its electron index is 1.9, quite similar to the TeV source in Fig. 3 at a comparable distance. The power-law slope is steeper than of HESS J1837−069 at 6.6 kpc, cf. Fig. 1; there is no interstellar absorption of the tachyon flux [22].
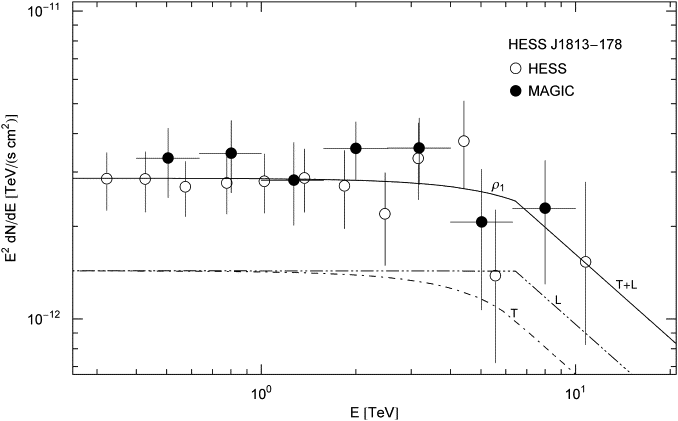
Fig. 3. Spectral map of the TeV γ-ray
source HESS J1813−178 coincident with supernova remnant W33. HESS flux
points from Ref. [9], MAGIC
points from Ref. [11]. Notation
as in Fig. 1. The
tachyonic cascade ρ1=T+L is
generated by the ultra-relativistic electron plasma of the remnant, cf.
Table 1. The
spectral break at ![]() separates the power-law slope from the extended GeV plateau distinctive
of tachyonic cascade spectra [21], [23] and [24].
separates the power-law slope from the extended GeV plateau distinctive
of tachyonic cascade spectra [21], [23] and [24].
Parameters of the nonthermal electron plasma generating the tachyonic cascade spectra of the TeV γ-ray sources in Fig. 1, Fig. 2 and Fig. 3.
α is the electron index, and γ1
the lower threshold Lorentz factor of the ultra-relativistic electron
populations, cf. after Eq. (5.1). ![]() determines the amplitude of the tachyon flux, from which the electron
count ne is inferred at the
indicated distance d, cf. Refs. [[27], [28] and [29]]. The
parameters α, γ1,
and
determines the amplitude of the tachyon flux, from which the electron
count ne is inferred at the
indicated distance d, cf. Refs. [[27], [28] and [29]]. The
parameters α, γ1,
and ![]() are extracted from the χ2-fit
T+L in the figures. The amplitude
are extracted from the χ2-fit
T+L in the figures. The amplitude ![]() is related to the electron number by
is related to the electron number by ![]() ,
cf. Ref. [7].
,
cf. Ref. [7].
Fig. 1 shows the
TeV spectral map of the unidentified TeV source HESS J1837−069 [9], coincident
with the pulsar wind nebula AX J1838.0−0655. The distance estimate to
this X-ray nebula is 6.6 kpc, by association with a nearby
cluster of red supergiants. Fig. 2 depicts
the spectral fit to the extended TeV source HESS J1834−087, associated
with the shell-type supernova remnant W41, cf. Refs. [9] and [10]. The
kinematic distance estimate of W41 is 4 kpc. Spectral plateaus
in the MeV to GeV range occur frequently in spectral maps of both
thermal and nonthermal TeV sources, and can easily be fitted with
tachyonic cascade spectra, in contrast to electromagnetic or hadronic
radiation models. Thermal spectra of γ-ray binaries such as binary
pulsars and microquasars are studied in Refs. [12] and [23], and a
thermal cascade fit of a γ-ray quasar is performed in Ref. [24]. The
shocked electron plasma of supernova remnants requires nonthermal
electron densities. Fig. 3 shows a
nonthermal cascade fit to the TeV source HESS J1813−178, located in the
vicinity of the H II region W33 [9] and [11] at a
distance of 4.5 kpc. The lower edge of Lorentz factors of the
electron plasma is γ1≈3.0×109,
inferred from the cascade fit. The corresponding electron and proton
energies are ![]() and
and ![]() .
These lower bounds on the energy of the radiating source particles are
to be compared to the spectral breaks in the cosmic-ray spectrum at 1015.5
and 1017.8 eV, dubbed knee and second
knee, respectively [25] and [26]. The bounds
are one order lower for the sources in Fig. 1 and Fig. 2, cf. Table 1, but in
all three remnants the lower bound on the proton energy is close to the
second knee.
.
These lower bounds on the energy of the radiating source particles are
to be compared to the spectral breaks in the cosmic-ray spectrum at 1015.5
and 1017.8 eV, dubbed knee and second
knee, respectively [25] and [26]. The bounds
are one order lower for the sources in Fig. 1 and Fig. 2, cf. Table 1, but in
all three remnants the lower bound on the proton energy is close to the
second knee.
6. Conclusion
We have studied the refraction of superluminal radiation at
dielectric interfaces, in particular the refraction angles for
transversal and longitudinal incidence, and the dependence of the
transmission and reflection coefficients on the polarization of the
incident radiation modes. Speed and energy of tachyonic quanta are
related by ![]() in vacuum, cf. after Eq. (2.12). At γ-ray
energies, their speed is close to the speed of light, the basic
difference to electromagnetic radiation being the longitudinally
polarized flux component. The polarization of tachyons can be
determined from the refraction angles at dielectric interfaces, cf.
after Eq. (4.1), or from
the reflection coefficients, which greatly differ for transversal and
longitudinal modes, cf. after Eq. (4.32). We
performed tachyonic cascade fits to the γ-ray
spectra of the TeV sources in Fig. 1, Fig. 2 and Fig. 3, and
disentangled the transversal and longitudinal flux components.
in vacuum, cf. after Eq. (2.12). At γ-ray
energies, their speed is close to the speed of light, the basic
difference to electromagnetic radiation being the longitudinally
polarized flux component. The polarization of tachyons can be
determined from the refraction angles at dielectric interfaces, cf.
after Eq. (4.1), or from
the reflection coefficients, which greatly differ for transversal and
longitudinal modes, cf. after Eq. (4.32). We
performed tachyonic cascade fits to the γ-ray
spectra of the TeV sources in Fig. 1, Fig. 2 and Fig. 3, and
disentangled the transversal and longitudinal flux components.
Shocked electron plasmas generate nonthermal γ-ray cascades typical for supernova remnants and pulsar wind nebulae. The characteristic feature is the extended spectral plateau at GeV energies, followed by a steep but barely bent spectral slope in the low TeV range, assuming a double-logarithmic and E2-rescaled flux representation as in Fig. 1, Fig. 2 and Fig. 3. The spectral maps discussed here are to be compared to the unpulsed γ-ray spectrum of the Crab Nebula, cf. Fig. 1 in Ref. [18], the spectral map of supernova remnant RX J1713.7−3946 in Fig. 2 of Ref. [18], the spectra of HESS J1825−137 and TeV J2032+4130 in Figs. 5 and 6 of Ref. [7], and the extended γ-ray cascade of supernova remnant W28 in Fig. 4 of Ref. [22]. All these spectra show GeV plateaus followed by straight or slightly curved power–law slopes. Traditional radiation mechanisms such as inverse Compton scattering or proton–proton scattering followed by pion decay fail to reproduce the extended plateaus in the spectral maps, a fact often concealed by compression in broadband maps. By contrast, tachyonic cascades provide excellent fits to the GeV plateaus and power–law slopes. The latter are a signature of shock-heated electron plasmas, and absent in the spectra of thermal γ-ray sources like TeV blazars [30] and [31], where the plateaus terminate in exponential decay without power–law transition. The spectral breaks at the join of the spectral plateaus and the power–law slopes are determined by the lower threshold Lorentz factors of the nonthermal source populations in the remnants. These Lorentz factors can be extracted from the spectral fits [32], and suggest that TeV γ-ray sources in Galactic supernova remnants are capable of accelerating protons to energies above the spectral break at 1017.8 eV in the cosmic-ray spectrum.
Acknowledgments
The author acknowledges the support of the Japan Society for the Promotion of Science. The hospitality and stimulating atmosphere of the Centre for Nonlinear Dynamics, Bharathidasan University, Trichy, and the Institute of Mathematical Sciences, Chennai, are likewise gratefully acknowledged. I also thank the referee for useful suggestions regarding substance as well as readability, which greatly helped to improve the initial draft.