Neutrino currents in the absolute spacetime: Relating the refractive index of the aether to the OPERA excess velocity
R. Tomaschitz 2012 EPL 97
39003
doi:10.1209/0295-5075/97/39003
Received 12 October 2011, accepted for publication 2 January 2012
Published 6 February 2012
Abstract
The superluminal neutrino velocity measured by the OPERA experiment is explained in a non-relativistic spacetime conception. Spacetime is viewed as a permeable medium of wave propagation. The neutrino wave equation is coupled to a permeability tensor, like electromagnetic fields in dielectric media. The inertial frame in which this tensor is isotropic defines a distinguished frame of reference, the rest frame of the aether. The dispersion relation of the spinorial wave modes gives rise to a superluminal group velocity of the energy flux. The Gordon decomposition of spinor currents in a refractive and dispersive spacetime is performed with finite as well as zero rest mass. The convective and spin components of the superluminal neutrino current are related to the permeability tensor. The refractive index of the aether depends on the neutrino energy, and is inferred in the 10 to 50GeV range from the measured excess velocity. Implications of the superluminal speed of signal transfer regarding relativity principles and causality are discussed.
Introduction
The OPERA experiment [1] measured a neutrino excess speed of υ/c-1 ≈2.48±0.6×10−5, at an average neutrino energy of 17GeV. This was inferred from a time-of-flight measurement, with a muon neutrino beam over a baseline of 730km between the source at CERN and the OPERA detector at the underground Gran Sasso Laboratory. We explain this excess speed in an absolute spacetime conception, by coupling the neutrino wave equation to the permeability tensor of the aether [2,3].
We discuss the coupling of Dirac spinors to a frequency-dependent permeability tensor, the relation to the Klein-Gordon equation in a dispersive spacetime, as well as the eikonal limit. The permeable spacetime gives rise to a superluminal group velocity. We analyze spinor currents in the aether, and perform the Gordon decomposition into a convection and spin component. The spin current is described in terms of a magnetization and polarization field. We relate the energy flux to the superluminal convection current and show that it propagates with group velocity in the aether.
Finally we identify the superluminal group velocity of a neutrino current with the OPERA excess velocities at three different frequencies, and find, by interpolation, the frequency variation of the refractive index of the aether for neutrinos in the 10–50GeV interval. In the conclusion, we further elaborate on the absolute spacetime, in particular on causality, inertial frames, and the rest frame of the aether as manifested by the isotropic cosmic microwave background radiation.
↑ CloseDirac equation coupled to the permeability tensor of the aether
We start with the Dirac Lagrangian
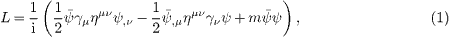
where we substitute a real symmetric permeability tensor for
the Minkowski metric, 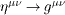 .
First, we assume that gμν
is constant. Standard Euler variation gives the Dirac equation and its
adjoint,
.
First, we assume that gμν
is constant. Standard Euler variation gives the Dirac equation and its
adjoint,
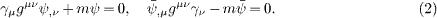
ψ†
indicates transposition and complex conjugation, and 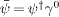 is
the adjoint 4-spinor. A subscript comma
followed by an index denotes a partial derivative,
is
the adjoint 4-spinor. A subscript comma
followed by an index denotes a partial derivative, 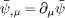 .
Indices are raised and lowered with the
Minkowski metric, ημν=diag(-1,
1, 1, 1), and we have put
.
Indices are raised and lowered with the
Minkowski metric, ημν=diag(-1,
1, 1, 1), and we have put 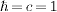 .
Greek indices run from 0 to 3, Latin ones from 1 to 3. The inverse of
the permeability tensor is denoted by gμν−1,
so that gμα−1gαν=δμ
ν, whereas gμν=ημα
gαβ ηβν.
The Dirac matrices satisfy γμ γν+γν
γμ=2ημν,
where γ0
is antihermitian and the γi
are hermitian [4].
.
Greek indices run from 0 to 3, Latin ones from 1 to 3. The inverse of
the permeability tensor is denoted by gμν−1,
so that gμα−1gαν=δμ
ν, whereas gμν=ημα
gαβ ηβν.
The Dirac matrices satisfy γμ γν+γν
γμ=2ημν,
where γ0
is antihermitian and the γi
are hermitian [4].
We will consider a homogeneous and isotropic permeability tensor, so that gμν is diagonal,
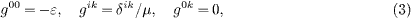
where ε and μ are real positive permeabilities, assumed to be constant at this point. The rest frame of the aether defines a distinguished frame of reference, a frame of absolute rest. This frame is physically manifested as the rest frame of the cosmic microwave background radiation, which is isotropic in this frame, with vanishing dipole anisotropy [5,6]. The Solar system barycenter is moving in this frame with a speed of 369km/s toward (l,b) ≈ (264.0°,48.26°) in Galactic coordinates [7–10]. The angle between the baseline of the neutrino beam and the velocity vector of the barycenter is periodically changing. This affects the superluminal neutrino speed measured in the rest frame of the barycenter, which can substantially differ from the neutrino speed in the aether frame. At superluminal velocities much higher than the speed of light, this angular dependence can even affect the causality interpretation. However, since the neutrino excess speed is very small and the velocity of the barycenter much smaller than the speed of light, we can assume that the measurement of the neutrino velocity is carried out in the rest frame of the microwave background, cf. the conclusion.
We perform a time separation of the wave field, using the
factorization 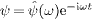 ,
,
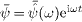 ,
where
,
where 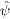 is
time independent, and use the permeability tensor (3)
to write the Lagrangian (1)
as
is
time independent, and use the permeability tensor (3)
to write the Lagrangian (1)
as
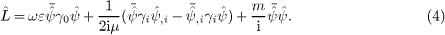
Time-separated quantities will be denoted by a hat.
Applying the Dirac operator γμ gμν ∂ν+m onto the first equation in (2), we recover the Klein-Gordon equation coupled to the permeability tensor,

where hμν=gμα ηαβgβν. The diagonal gμν in (3) gives h00=−ε2, hik=δik /μ2, h0k=0. When time-separated, this reads
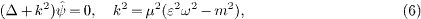
where Δ is the Euclidean Laplace operator, and the time-separated Dirac equations (2) are
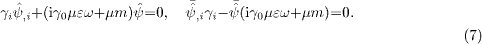
These equations can directly be derived by Euler variation of
the Lagrangian (4).
From now on, we take 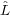 in (4)
and the Dirac equations (7)
as starting point (instead of (1)
and (2)),
and substitute frequency-dependent permeabilities ε (ω)
and μ
(ω). Moreover, applying the operator γi
∂i+(iγ0
ωμ ε+μm) onto the first
equation in (7),
one can derive the time-separated Klein-Gordon equation (6)
with frequency-dependent permeabilities. If the spinor is a plane-wave
solution
in (4)
and the Dirac equations (7)
as starting point (instead of (1)
and (2)),
and substitute frequency-dependent permeabilities ε (ω)
and μ
(ω). Moreover, applying the operator γi
∂i+(iγ0
ωμ ε+μm) onto the first
equation in (7),
one can derive the time-separated Klein-Gordon equation (6)
with frequency-dependent permeabilities. If the spinor is a plane-wave
solution 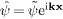 of (7),
where
of (7),
where 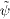 is
a constant 4-spinor, it also satisfies (6),
which requires the dispersion relation
is
a constant 4-spinor, it also satisfies (6),
which requires the dispersion relation

connecting the wave number k(ω )=|k| with the permeabilities. A positive squared wave number implies the frequency condition ε (ω )>m/|ω |. Dispersion is modeled by frequency-dependent permeabilities in time-separated quantities [11,12]. The dispersion relation (8) also follows from the Hamilton-Jacobi equation, hμν S,μ S,ν+m2=0, since ψ∝ eiS, with the action S=k(ω )x-ωt, so that the semiclassical approximation of (5) is exact: the phase of the quantum-mechanical elementary waves is the classical action or eikonal.
The permeability tensor gμν in the Dirac equation (2) is unrelated to electromagnetic permeabilities, even though the formalism resembles that of electromagnetic fields in dielectrics. Electromagnetic radiation is not affected by the permeability tensor of neutrinos. In fact, this would even contradict the Michelson-Morley experiment. Different particles couple with different permeability tensors to the aether.
↑ CloseConvection and spin currents in the dispersive spacetime
We start with a constant permeability tensor gμν,
and consider two solutions ψ and 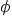 of the Dirac
equation (2),
so that the current
of the Dirac
equation (2),
so that the current 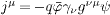 is
conserved, ∂μ jμ=0.
q
is some charge carried by the current. The charge density is defined by
ρ=j0.
Using the diagonal permeability tensor (3)
(frequency independent), we find
is
conserved, ∂μ jμ=0.
q
is some charge carried by the current. The charge density is defined by
ρ=j0.
Using the diagonal permeability tensor (3)
(frequency independent), we find 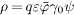 ,
,
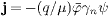 ,
and the continuity equation ∂ρ /∂t+div
j=0.
,
and the continuity equation ∂ρ /∂t+div
j=0.
To derive the continuity equation in the case of frequency-dependent permeabilities, we employ the time-separated Dirac equations,
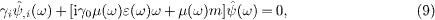
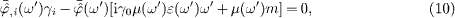
so that the divergence 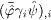 vanishes
at ω'=ω.
The
spinors
vanishes
at ω'=ω.
The
spinors 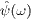 and
and
 also
satisfy the Klein-Gordon
equation (6)
with dispersion relation (8).
The time-dependent Fourier modes are
also
satisfy the Klein-Gordon
equation (6)
with dispersion relation (8).
The time-dependent Fourier modes are 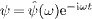 and
and
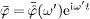 .
If not indicated otherwise,
.
If not indicated otherwise, 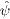 means
means
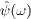 and
and
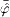 stands
for
stands
for 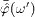 .
.
We use the time separation 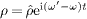 and
and
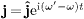 ,
and define the current as
,
and define the current as
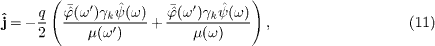
which coincides with 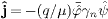 stated
above for constant permeabilities. In
the first term, we substitute the adjoint Dirac equation (10),
and use (9)
in the second term, to decompose the current into a convection and a
spin current,
stated
above for constant permeabilities. In
the first term, we substitute the adjoint Dirac equation (10),
and use (9)
in the second term, to decompose the current into a convection and a
spin current, 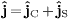 ,
cf. [13,14],
,
cf. [13,14],
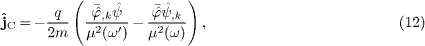
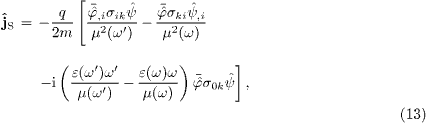
where σμν=(γμ
γν−γν γμ
)/2, so that γμ γν=ημν+σμν.
We also split the charge density into a convection and a spin density, 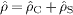 ,
and use the time separation
,
and use the time separation 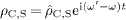 ,
,
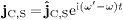 .
The time derivatives of
.
The time derivatives of 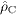 and
and
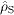 are
defined by separate continuity equations, ∂ρ C /∂t=−div
jC,
∂ρ
S /∂t=−div jS,
so that a time integration gives
are
defined by separate continuity equations, ∂ρ C /∂t=−div
jC,
∂ρ
S /∂t=−div jS,
so that a time integration gives

Here, we substitute the current component (12),
and perform the limit 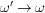 by
expanding in powers of ω'-ω, to find
the convection density
by
expanding in powers of ω'-ω, to find
the convection density

where k2
is defined in (8),
and both fields 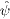 and
and
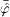 are
taken at ω. The second
term in (15)
can be rewritten via the Klein-Gordon equation (6),
are
taken at ω. The second
term in (15)
can be rewritten via the Klein-Gordon equation (6),
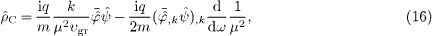
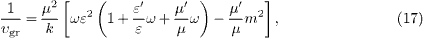
where υgr is the group velocity

with k(ω) in (8). The second term in (16) is a divergence, which drops out in a spatial integration or for plane waves. The phase velocity is υph=ω/k, and the refractive index is defined as the inverse phase velocity, nr=k/ω.
We consider plane-wave solutions of the Dirac
equations (9)
and (10)
at ω'=ω:
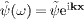 and
and
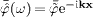 ,
where k=k(ω
)k0,
cf. (8).
We find, cf. (12)
and (16),
,
where k=k(ω
)k0,
cf. (8).
We find, cf. (12)
and (16),
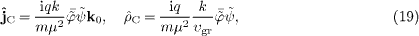
and 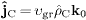 ,
so that the charge transfer happens at
group velocity.
,
so that the charge transfer happens at
group velocity.
The charge density of the spin current 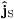 in (13)
is obtained in like manner, via the time integration (14),
in (13)
is obtained in like manner, via the time integration (14),
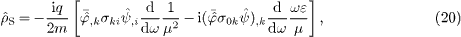
where the adjoint field 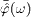 is
taken at ω'=ω. We write
is
taken at ω'=ω. We write 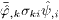 as
a divergence, symmetrize, and use the
Dirac equations (9)
and (10)
to obtain
as
a divergence, symmetrize, and use the
Dirac equations (9)
and (10)
to obtain
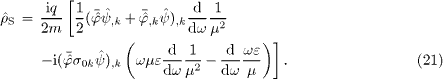
The spin density 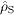 is
the divergence of a polarization field,
is
the divergence of a polarization field, 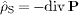 ,
,
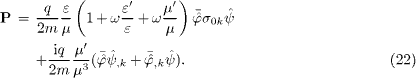
The spin current 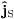 in (13)
at ω'=ω
is a magnetization current,
in (13)
at ω'=ω
is a magnetization current,
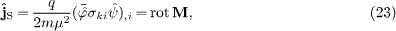
where the magnetization field reads
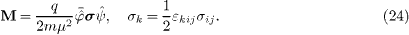
Here, we defined a spin vector 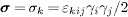 ,
where εkij
is the Levi-Civita symbol.
,
where εkij
is the Levi-Civita symbol. 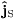 vanishes
for plane waves, and so does
vanishes
for plane waves, and so does 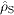 .
If we refrain from performing the limit
.
If we refrain from performing the limit 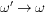 in (14),
a polarization current ∂P/∂t
has to be added to rotM
in (23);
at ω'=ω
the polarization field (22)
is time independent.
in (14),
a polarization current ∂P/∂t
has to be added to rotM
in (23);
at ω'=ω
the polarization field (22)
is time independent.
Conservation of energy in the aether
In the case of a constant permeability tensor gμν, the energy-momentum tensor of the Dirac field is obtained by standard Lagrange formalism [15,16],
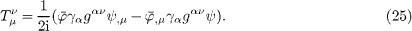
This tensor satisfies the conservation law Tμ,
νν=0,
provided that the fields ψ and 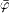 solve
the Dirac equation and the permeability tensor gαν
is constant. The components T0ν
define the energy density T00
and energy flux T0i.
We specify the permeability tensor as in (3)
(frequency independent) and split off time, writing
solve
the Dirac equation and the permeability tensor gαν
is constant. The components T0ν
define the energy density T00
and energy flux T0i.
We specify the permeability tensor as in (3)
(frequency independent) and split off time, writing 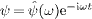 ,
,
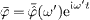 and
and
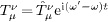 .
The fields
.
The fields 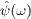 and
and
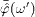 satisfy
the time-separated Dirac
equations (9)
and (10).
We thus find
satisfy
the time-separated Dirac
equations (9)
and (10).
We thus find
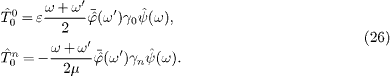
Next, we consider a dispersive spacetime with frequency-dependent permeabilities ε (ω) and μ (ω), and define the flux vector as
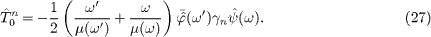
At ω'=ω, we may
write 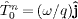 ,
with current
,
with current  in (11).
Here, we substitute the Gordon decomposition
in (11).
Here, we substitute the Gordon decomposition 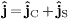 ,
cf. (12)
and (13).
We obtain the energy density
,
cf. (12)
and (13).
We obtain the energy density 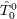 by
applying the time integration (14)
and performing the limit
by
applying the time integration (14)
and performing the limit  ,
,
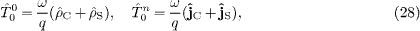
with the convection and spin densities 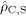 in (16)
and (21).
On substituting plane-wave solutions as in (19),
we find
in (16)
and (21).
On substituting plane-wave solutions as in (19),
we find  ,
,
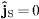 ,
as well as
,
as well as 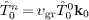 ,
where k0
is the unit wave vector. The energy flux propagates in the dispersive
aether with group velocity υgr,
cf. (17).
,
where k0
is the unit wave vector. The energy flux propagates in the dispersive
aether with group velocity υgr,
cf. (17).
Spinorial wave propagation in the aether with zero rest mass
In the massless limit, the convection and spin densities
in (16)
and (21)
become singular, and we have to proceed differently. We put m=0
in the Dirac equations (9)
and (10),
and multiply by γ0.
The spinors 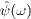 and
and
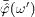 satisfy
the Klein-Gordon equation (6)
with dispersion relation k2=ε2
(ω )μ2 (ω )ω2,
cf. (8).
satisfy
the Klein-Gordon equation (6)
with dispersion relation k2=ε2
(ω )μ2 (ω )ω2,
cf. (8).
We start with current  in (11).
In the first term, we replace
in (11).
In the first term, we replace  by
way of the adjoint Dirac
equation (10),
and in the second term we substitute (9)
for
by
way of the adjoint Dirac
equation (10),
and in the second term we substitute (9)
for 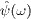 ,
to split the current into a convection and
spin component,
,
to split the current into a convection and
spin component, 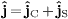 ,
,
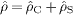 ,
where, cf. (12)
and (13),
,
where, cf. (12)
and (13),
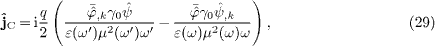
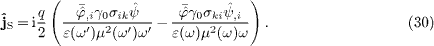
The charge densities 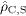 are
calculated via the time
integration (14)
and by performing the limit
are
calculated via the time
integration (14)
and by performing the limit  and
making use of the Klein-Gordon equation (6).
The convection density reads
and
making use of the Klein-Gordon equation (6).
The convection density reads
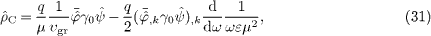
where υgr
is the group velocity in (17)
taken at m=0,
so that 1/υgr=εμ+(εμ )'ω.
Using plane waves  ,
,
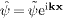 ,
we find
,
we find
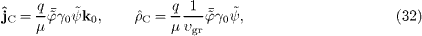
and thus 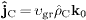 .
We may replace
.
We may replace 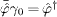 ,
where
,
where 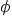 †
denotes the transposed and conjugated spinor. The charge transfer
happens with group velocity, and the refractive index for zero rest
mass is nr=k/ω=εμ,
cf. [3,17].
†
denotes the transposed and conjugated spinor. The charge transfer
happens with group velocity, and the refractive index for zero rest
mass is nr=k/ω=εμ,
cf. [3,17].
The charge density of the spin current 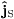 in (30)
reads, cf. (14),
in (30)
reads, cf. (14),
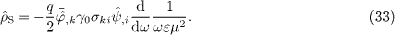
We symmetrize the divergence 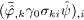 ,
and use the
masslessDiracequations (9)and (10)aswellas
,
and use the
masslessDiracequations (9)and (10)aswellas
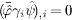 ,
to write this as a polarization density
,
to write this as a polarization density 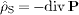 ,
,
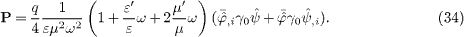
The spin current 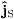 in (30)
is a magnetization current,
in (30)
is a magnetization current,
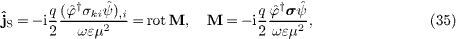
with spin vector 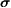 defined
in (24).
defined
in (24).
Refractive index and neutrino excess velocity
The goal is to relate the OPERA excess velocity to the refractive index nr of the aether, cf. after (18) and (32). In the massless limit, the group velocity (17) reads

where nr=ε (ω )μ (ω), cf. (3) and (8). A possible neutrino rest mass of a few eV is negligible given the GeV energy range of the OPERA experiment. I also mention that a negative mass-square is not an option in the Dirac equation, as mass enters linearly and an imaginary mass destroys the hermiticity of the energy operator [4].
At 28.2GeV, an excess speed of υgr−1 ≈ (2.51 ± 0.6)×10−5 was measured for muon neutrinos. At 13.8GeV and 40.7GeV, the excess speed was υgr−1 ≈ 2.25×10−5 and υgr−1 ≈ 2.80×10−5, respectively, inferred from the time-of-flight differences δt28.2 ≈ 61.1 ns, δt13.8 ≈ 54.7 ns, and δt40.7 ≈ 68.1 ns, where δt=τc−τν is the difference of the photon and neutrino time of flight [1]. A baseline estimate of 730.085km was used, resulting in a photon time of flight of τc ≈ 2.43530×106 ns. The excess velocities are found via υgr−1=δt/(τc−δt). The independent MINOS experiment [18] measured a neutrino excess speed of υgr−1 ≈ (5.1 ± 2.9)×10−5 at a peak energy of 3GeV. The neutrino flux from supernova SN1987A at 10MeV did not exhibit a deviation from the vacuum speed of light [19–21].
We use the OPERA excess velocities to determine the frequency variation of the refractive index nr (ω) in the 10–50GeV range. To this end, we expand nr (ω) at the average energy ω0 ≈ 28.2 GeV into a truncated Taylor series (or Laurent series if needed),
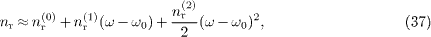
and substitute this into (36). We obtain three linear equations for the expansion coefficients nr(0,1,2) (ω0), if we use for ω the neutrino energies of 28.2GeV, 13.8GeV and 40.7GeV, and for υgr−1 the respective excess velocities. Solving this system, we find 1-nr(0) (ω0 ) ≈ 2.27×10−5, as well as the derivatives nr(1) (ω0 ) ≈−8.61×10−8 GeV−1 and nr(2) (ω0 ) ≈−1.27×10−9 GeV−2. These small derivatives justify expansion (37) in the 10–50GeV range. On substituting the coefficients nr(0,1,2) (ω0) into (37), we obtain the frequency variation of the refractive index in this interval. For instance, 1-nr (28.2 GeV)=2.27×10−5, 1-nr (13.8 GeV )=2.16×10−5, and 1-nr (40.7 GeV)=2.38×10−5, in accordance with the mild variation of the excess velocities at these energies. If we extrapolate further down to 3GeV, the energy of the MINOS experiment, we find, via (36) and (37), υgr−1 ≈ 2.11×10−5 at 3GeV. This is still marginally consistent with the MINOS excess speed (5.1 ± 2.9)×10−5.
The mentioned SN result at 10MeV is a null result consistent
with the speed of light [21].
At this energy, the permeability tensor (3)
coincides with the Minkowski metric. Accordingly, there is a
substantial frequency variation of the permeabilities between 3GeV and
10MeV. As there are no data points available in this energy range, I do
not specify the permeabilities in this range, which have to be inferred
from an empirical fit. If υgr (ω)
is known over an extended energy range, one can obtain the refractive
index by a numerical quadrature of (36),
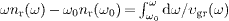 ,
where the integration constant nr
(ω0) is calculated
locally as above, by means of a truncated Taylor expansion.
,
where the integration constant nr
(ω0) is calculated
locally as above, by means of a truncated Taylor expansion.
Conclusion
The OPERA excess velocity amounts to superluminal signal transfer, which is causality violating in a relativistic spacetime view based on the relativistic interpretation of the Lorentz symmetry of Maxwell's equations [22,23]. Causality implies that every effect has a cause, that the cause precedes the effect, and that the distinction of cause and effect is unambiguous. The third condition means that every observer can arrive at the same conclusion as to what is cause and effect. If two events (cause and effect) are related by the emission and absorption of a superluminal signal, this establishes a spacelike connection. One can always find a Lorentz boost which overturns the time order of this connection. Two inertial observers related by this Lorentz boost will see a different time order in their proper time, and arrive at the opposite conclusion as to what is cause and effect. This does not depend on the specific physical mechanism of the signal transfer. Superluminal signal transfer is tantamount to a spacelike connection, and the time order in spacelike connections is ambiguous, as it can be altered by a Lorentz transformation. Thus, any kind of superluminal signal transfer is causality violating in a relativistic context, since, according to the relativity principle, the contradictory conclusions of the two inertial observers are equally valid. Therefore, a distinguished frame of reference is required, to which all uniformly moving inertial observers can relate and arrive at an unambiguous causality interpretation of their observations, even though the cosmic time order of events may be inverted in their proper time. We have identified this distinguished frame as the rest frame of the aether, in which the cosmic microwave background is isotropic, and which determines the absolute cosmic time order [5,6,24]. This discussion can be made quantitative quite easily, as the causality of superluminal signal transfer does not depend on the specific realization of the signal.
The coordinates of the rest frame of the aether are denoted by
(t,x).
The world lines of source and detector read 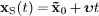 and
and
 ,
respectively. The rest frame of source and
detector is denoted by primed coordinates (t',x'),
and connected to the aether frame by a proper orthochronous Lorentz
boost,
,
respectively. The rest frame of source and
detector is denoted by primed coordinates (t',x'),
and connected to the aether frame by a proper orthochronous Lorentz
boost,
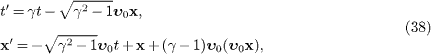
where  is
the velocity unit vector of source and
detector,
is
the velocity unit vector of source and
detector, 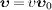 ,
and γ=(1-υ2)−1/2,
so that
,
and γ=(1-υ2)−1/2,
so that 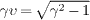 .
The source and detector world lines (t'S
,x'S)
and (t'D
,x'D)
in the primed frame can be parametrized by
.
The source and detector world lines (t'S
,x'S)
and (t'D
,x'D)
in the primed frame can be parametrized by
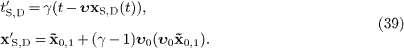
In the aether frame, a superluminal signal is emitted at (t0
,xS (t0
)), and absorbed at a later instant t1>t0
at (t1
,xD (t1
)). The speed of this signal is assumed to be
constant, 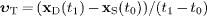 ,
and tachyonic, υT> 1,
so that a spacelike connection is established between emission and
absorption. In the primed frame, the emission and absorption events
take place at (t'0
,x'S)
and (t'1
,x'D),
respectively, where t'0=t'S
(t0)
and t'1=t'D
(t1),
cf. (39).
The time interval between emission t'0
and absorption t'1
in the rest frame of source and detector is
,
and tachyonic, υT> 1,
so that a spacelike connection is established between emission and
absorption. In the primed frame, the emission and absorption events
take place at (t'0
,x'S)
and (t'1
,x'D),
respectively, where t'0=t'S
(t0)
and t'1=t'D
(t1),
cf. (39).
The time interval between emission t'0
and absorption t'1
in the rest frame of source and detector is

We may write 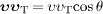 ,
where
,
where 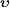 and
and
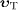 denote
velocities in the aether frame,
denote
velocities in the aether frame, 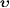 being
the velocity of the source and the
detector and
being
the velocity of the source and the
detector and 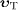 the
tachyonic (superluminal) signal speed. υT
corresponds to υgr
in (36).
A subluminal source moving with velocity
the
tachyonic (superluminal) signal speed. υT
corresponds to υgr
in (36).
A subluminal source moving with velocity 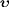 in
the aether frame can only emit
superluminal signals of velocity
in
the aether frame can only emit
superluminal signals of velocity 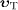 if
the condition
if
the condition 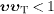 is
satisfied. This condition is required by
causality, in addition to kinematic constraints due to energy-momentum
conservation, and is also necessary for absorption. If an observer
moves with velocity
is
satisfied. This condition is required by
causality, in addition to kinematic constraints due to energy-momentum
conservation, and is also necessary for absorption. If an observer
moves with velocity 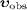 in
the aether frame, he will see the time
order of emission and absorption inverted in his proper time,
in
the aether frame, he will see the time
order of emission and absorption inverted in his proper time, 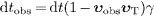 ,
if the angle between
,
if the angle between 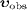 and
and
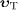 is
acute and the superluminal signal speed
sufficiently high.
is
acute and the superluminal signal speed
sufficiently high.
The causality of superluminal signal transfer is solely determined by the time order in the aether frame, in particular it does not depend on the energy concept. In the rest frame of the aether, sub- as well as superluminal particles or radiation quanta have positive energy, and energy-momentum conservation applies. The positivity of energy of a subluminal particle (with positive mass square) is preserved under a Lorentz transformation, which is not the case for tachyonic quanta, so that superluminal emission can result in energy gain in the rest frame of the emitting subluminal particle, if causality is violated [25].
The speed of the superluminal signal in the primed rest frame
of source and detector is 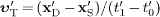 ,
where, cf. (39),
,
where, cf. (39),

Here, we split the superluminal speed 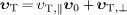 into
components parallel and orthogonal to
the unit vector
into
components parallel and orthogonal to
the unit vector 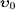 ,
and substitute (40)
for t1−t0
to obtain
,
and substitute (40)
for t1−t0
to obtain
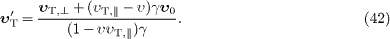
We multiply with 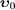 to
find
to
find 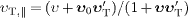 ,
substitute this into (42)
and solve for
,
substitute this into (42)
and solve for 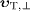 .
Thus,
.
Thus, 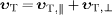 ,
where
,
where
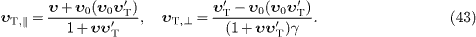
By means of this addition law, we can infer the superluminal
speed 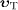 in
the aether frame from the measured speed
in
the aether frame from the measured speed 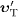 in
the rest frame of the source (and
detector) and the measured speed
in
the rest frame of the source (and
detector) and the measured speed 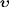 of
this rest frame in the aether.
Expanding (43)
in powers of υ, we find
of
this rest frame in the aether.
Expanding (43)
in powers of υ, we find
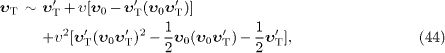
up to terms of O(υ3).
We square this and substitute 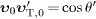 to
obtain
to
obtain
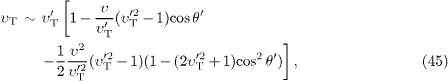
where 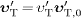 .
In the example discussed in this article, υ'T
is the measured neutrino speed, in units of the speed of light, and υ
is the speed of the Solar system barycenter or neutrino baseline
(neglecting the Earth's relative motions, which are at least one order
of magnitude smaller than υ) in the
aether. Since υ'T−1 ≈ 2.5×10−5
and υ≈
369 kms−1/c≈ 1.2×10−3,
we find υT ≈υ 'T
(1-6×10−8cosθ').
Thus, in view of the current error bound on υ'T−1 ≈ (2.5 ± 0.6)×10−5,
the superluminal speed υT
in the aether frame can be identified with the actually measured speed υ'T,
irrespectively of the periodically varying angle cosθ'
between the neutrino baseline and the velocity of the barycenter.
However, this angle becomes significant if the error bound is reduced
by two orders. In any case, if υ'T>>
1 or υ~1, the
velocities
.
In the example discussed in this article, υ'T
is the measured neutrino speed, in units of the speed of light, and υ
is the speed of the Solar system barycenter or neutrino baseline
(neglecting the Earth's relative motions, which are at least one order
of magnitude smaller than υ) in the
aether. Since υ'T−1 ≈ 2.5×10−5
and υ≈
369 kms−1/c≈ 1.2×10−3,
we find υT ≈υ 'T
(1-6×10−8cosθ').
Thus, in view of the current error bound on υ'T−1 ≈ (2.5 ± 0.6)×10−5,
the superluminal speed υT
in the aether frame can be identified with the actually measured speed υ'T,
irrespectively of the periodically varying angle cosθ'
between the neutrino baseline and the velocity of the barycenter.
However, this angle becomes significant if the error bound is reduced
by two orders. In any case, if υ'T>>
1 or υ~1, the
velocities 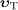 and
and
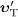 can
substantially differ depending on this
angle, cf. (45).
can
substantially differ depending on this
angle, cf. (45).
Wave fields propagating in the aether are coupled by permeability tensors, which are a manifestation of the microscopic space structure [3,22]. Here, we have discussed the permeability tensor for neutrinos, and explained the coupling of the Dirac equation to this tensor. We have studied freely propagating spinorial wave modes in the aether, and shown that the frequency-dependent refractive index gives rise to superluminal energy transfer. The OPERA excess velocities measured at GeV energies allow to derive a quantitative estimate of the refractive index of the aether for superluminal neutrinos in this energy range.
↑ CloseReferences
- [1]
- Adam T. et al 2011 arXiv:1109.4897
- [2]
- Tomaschitz R. 1998 Chaos, Solitons
Fractals 9 1199
- [3]
- Tomaschitz R. 2001 Class. Quantum Grav. 18 4395
- [4]
- Tomaschitz R. 2005 Eur. Phys. J. D
32 241
- [5]
- Tomaschitz R. 2003 Physica A
320 329
- [6]
- Tomaschitz R. 2007 Ann. Phys. (N. Y.)
322 677
- [7]
- Kogut A. et al 1993 Astrophys.
J. 419 1
- [8]
- Fixsen D. J. et al 1996 Astrophys. J. 473 576
- [9]
- Hinshaw G. et al 2009 Astrophys. J., Suppl. Ser. 180 225
- [10]
- Jarosik N. et al 2011 Astrophys. J., Suppl. Ser. 192 14
- [11]
- Landau L. D. and Lifshitz E. M. 1984 Electrodynamics
of Continuous Media (Oxford: Pergamon)
- [12]
- Tomaschitz R. 2010 Eur. Phys. J. C
69 241
- [13]
- Bjorken J. D. and Drell S. D. 1964 Relativistic
Quantum Mechanics (New York: McGraw-Hill)
- [14]
- Halzen F. and Martin A. D. 1984 Quarks
and Leptons (New York: Wiley)
- [15]
- Wentzel G. 1949 Quantum Theory of
Fields (New York: Interscience Publishers)
- [16]
- Bjorken J. D. and Drell S. D. 1965 Relativistic
Quantum Fields (New York: McGraw-Hill)
- [17]
- Tomaschitz R. 2009 Physica B
404 1383
- [18]
- Adamson P. et al 2007 Phys.
Rev. D 76 072005
- [19]
- Hirata K. et al 1987 Phys.
Rev. Lett. 58 1490
- [20]
- Bionta R. M. et al 1987 Phys.
Rev. Lett. 58 1494
- [21]
- Longo M. J. 1987 Phys. Rev. D
36 3276
- [22]
- Tomaschitz R. 1996 Chaos, Solitons
Fractals 7 753
- [23]
- Tomaschitz R. 2000 Celest. Mech. Dyn.
Astron. 77 107
- [24]
- Tomaschitz R. 2004 Chaos, Solitons
Fractals 20 713
- [25]
- Tomaschitz R. 2000 Int. J. Mod. Phys.
A 15 3019
-
Contents
- [1]
- Adam T. et al 2011 arXiv:1109.4897 Preprint
- [2]
- Tomaschitz R. 1998 Chaos, Solitons
Fractals 9 1199 CrossRef
- [3]
- Tomaschitz R. 2001 Class. Quantum Grav. 18 4395 IOPscience
- [4]
- Tomaschitz R. 2005 Eur. Phys. J. D
32 241 CrossRef
- [5]
- Tomaschitz R. 2003 Physica A
320 329 CrossRef
- [6]
- Tomaschitz R. 2007 Ann. Phys. (N. Y.)
322 677 CrossRef
- [7]
- Kogut A. et al 1993 Astrophys.
J. 419 1 CrossRef
- [8]
- Fixsen D. J. et al 1996 Astrophys. J. 473 576 IOPscience
- [9]
- Hinshaw G. et al 2009 Astrophys. J., Suppl. Ser. 180 225 IOPscience
- [10]
- Jarosik N. et al 2011 Astrophys. J., Suppl. Ser. 192 14 IOPscience
- [11]
- Landau L. D. and Lifshitz E. M. 1984 Electrodynamics
of Continuous Media (Oxford: Pergamon)
- [12]
- Tomaschitz R. 2010 Eur. Phys. J. C
69 241 CrossRef
- [13]
- Bjorken J. D. and Drell S. D. 1964 Relativistic
Quantum Mechanics (New York: McGraw-Hill)
- [14]
- Halzen F. and Martin A. D. 1984 Quarks
and Leptons (New York: Wiley)
- [15]
- Wentzel G. 1949 Quantum Theory of
Fields (New York: Interscience Publishers)
- [16]
- Bjorken J. D. and Drell S. D. 1965 Relativistic
Quantum Fields (New York: McGraw-Hill)
- [17]
- Tomaschitz R. 2009 Physica B
404 1383 CrossRef
- [18]
- Adamson P. et al 2007 Phys.
Rev. D 76 072005 CrossRef
- [19]
- Hirata K. et al 1987 Phys.
Rev. Lett. 58 1490 CrossRef
PubMed
- [20]
- Bionta R. M. et al 1987 Phys.
Rev. Lett. 58 1494 CrossRef
PubMed
- [21]
- Longo M. J. 1987 Phys. Rev. D
36 3276 CrossRef
- [22]
- Tomaschitz R. 1996 Chaos, Solitons
Fractals 7 753 CrossRef
- [23]
- Tomaschitz R. 2000 Celest. Mech. Dyn.
Astron. 77 107 CrossRef
- [24]
- Tomaschitz R. 2004 Chaos, Solitons
Fractals 20 713 CrossRef
- [25]
- Tomaschitz R. 2000 Int. J. Mod. Phys.
A 15 3019