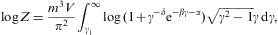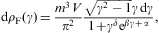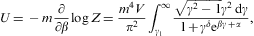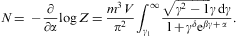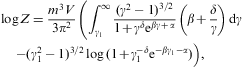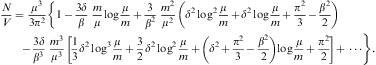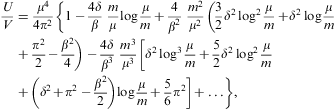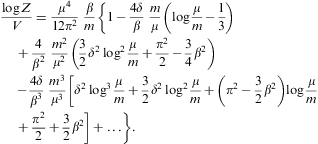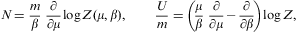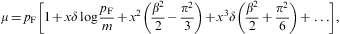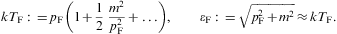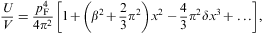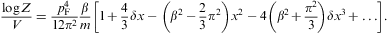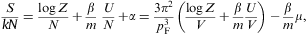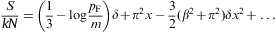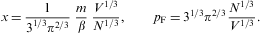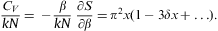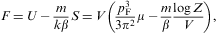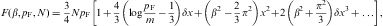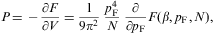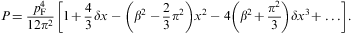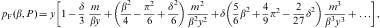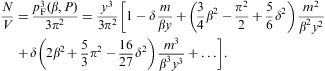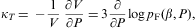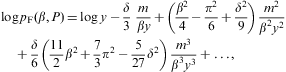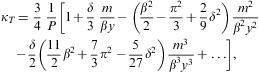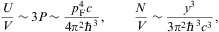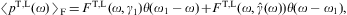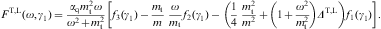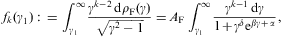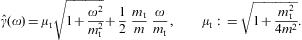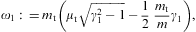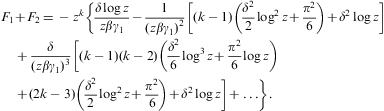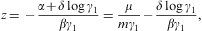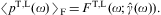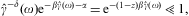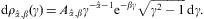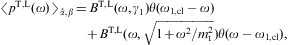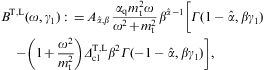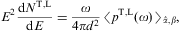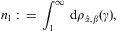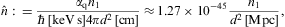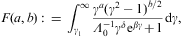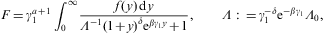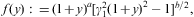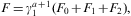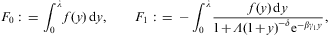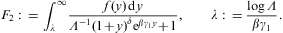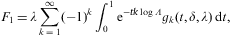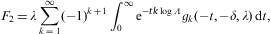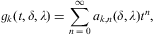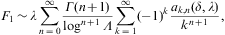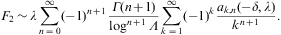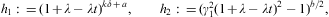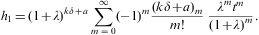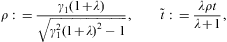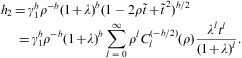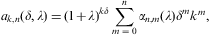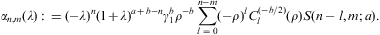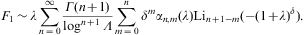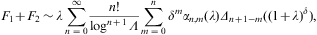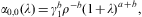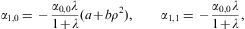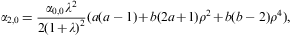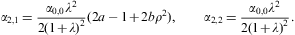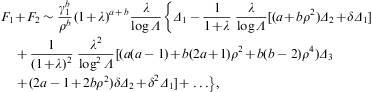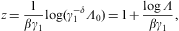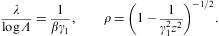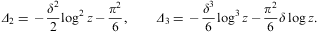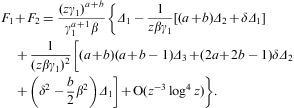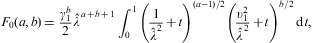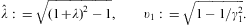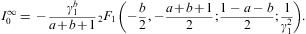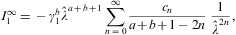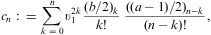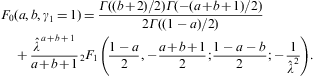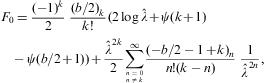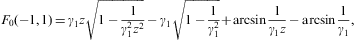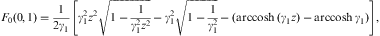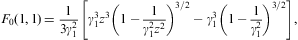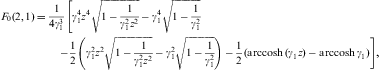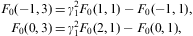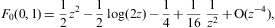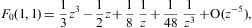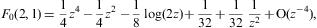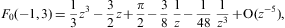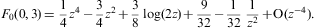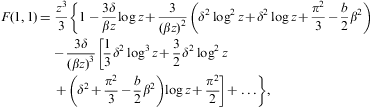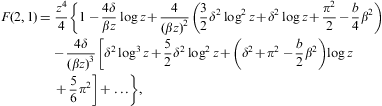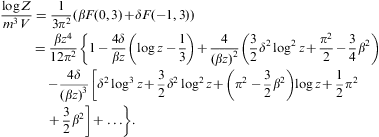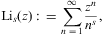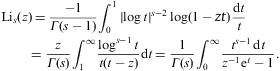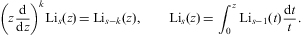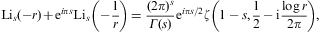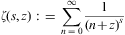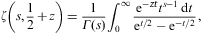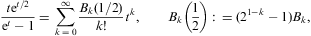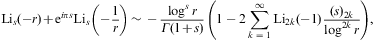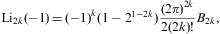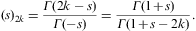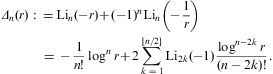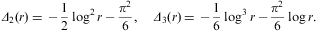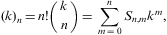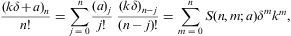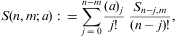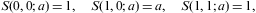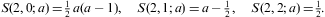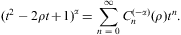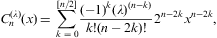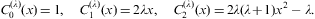Volume 405, Issue 3, 1 February 2010, Pages 1022-1032
Roman
Tomaschitz ,
a,
,
a,

Abstract
Polylogarithmic fugacity expansions of the partition function, the caloric and thermal equations of state, and the specific heat of fermionic power-law distributions are derived in the nearly degenerate low-temperature/high-density quantum regime. The spectral functions of an ultra-relativistic electron plasma are obtained by averaging the tachyonic radiation densities of inertial electrons with Fermi power-laws, whose entropy is shown to be extensive and stable. The averaged radiation densities are put to test by performing tachyonic cascade fits to the γ-ray spectrum of the TeV blazar Markarian 421 in a low and high emission state. Estimates of the thermal electron plasma in this active galactic nucleus are extracted from the spectral fits, such as temperature, number count, and internal energy. The tachyonic cascades reproduce the quiescent as well as a burst spectrum of the blazar obtained with imaging atmospheric Cherenkov detectors. Double-logarithmic plots of the differential tachyon flux exhibit intrinsic spectral curvature, caused by the Boltzmann factor of the electron gas.
Keywords: Fermi power-law ensembles; Nearly degenerate electron plasma; Superluminal radiation; Tachyonic cascade spectra; Spectral curvature; γ-Ray blazars; Negative mass-square; Transversal and longitudinal radiation modes; Polylogarithms
PACS classification codes: 52.25.Kn; 52.27.Ny; 71.10.Ca; 95.30.Tg
Article Outline
- 1. Introduction
- 2. Ultra-relativistic Fermi power laws
- 3. Thermodynamic variables of nearly degenerate power-law distributions
- 4. Tachyonic cascade spectra
- 5. Conclusion
- Acknowledgements
- Appendix A. Incomplete integrals of fermionic power-law densities
- A.1. Fugacity expansion at low temperature and high density
- A.2. Zero-temperature degeneracy
- A.3. Number count, internal energy, and partition function in the nearly degenerate regime
- Appendix B. Polylogarithms, Stirling numbers, and Gegenbauer polynomials
- References
1. Introduction
Electronic power-law distributions are commonly used in electromagnetic spectral averages to model the synchrotron emission of astrophysical plasmas, such as the magnetospheric X-ray emission of planets [1]. In this article, we discuss spectral fitting based on fermionic power-law distributions, and develop the thermodynamic formalism of power-law ensembles quantized in Fermi–Dirac statistics. The quasiclassical fugacity expansion pertinent to fermionic power-law distributions in the high-temperature/low-density regime was derived in Ref. [2]. Here, we investigate the opposite asymptotic limit, nearly degenerate ultra-relativistic power-law ensembles in the low-temperature/high-density quantum regime. The efficiency of the spectral averages is demonstrated by applying tachyonic cascade fits to the TeV blazar Mkn 421 in a low emission state and in outburst. The cascade spectra are obtained by averaging the tachyonic radiation densities of individual electrons over ultra-relativistic electron populations in the galactic nucleus. The thermodynamic parameters of the electron plasma are extracted from the spectral fits.The tachyonic radiation field is a real Proca field with
negative mass-square, ![]() ,
subject to the Lorentz condition
,
subject to the Lorentz condition ![]() ,
where mt
is the mass of the superluminal Proca field Aμ,
and q the tachyonic charge carried by the
subluminal electron current
,
where mt
is the mass of the superluminal Proca field Aμ,
and q the tachyonic charge carried by the
subluminal electron current ![]() [3]. In the
Proca equation, the mass term is added with a positive sign, and the
sign convention for the d’Alembertian is ∂ν∂ν=Δ-∂2/∂t2,
so that
[3]. In the
Proca equation, the mass term is added with a positive sign, and the
sign convention for the d’Alembertian is ∂ν∂ν=Δ-∂2/∂t2,
so that ![]() is the negative mass-square of the radiation field. The negative
mass-square refers to the radiation field rather than the current, in
contrast to traditional theories based on superluminal source particles
emitting electromagnetic radiation [4], [5], [6] and [7]. Estimates
of the tachyon–electron mass ratio and the tachyonic fine structure
constant are mt/m≈1/238
and q2/(4π
is the negative mass-square of the radiation field. The negative
mass-square refers to the radiation field rather than the current, in
contrast to traditional theories based on superluminal source particles
emitting electromagnetic radiation [4], [5], [6] and [7]. Estimates
of the tachyon–electron mass ratio and the tachyonic fine structure
constant are mt/m≈1/238
and q2/(4π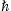 c)≈1.0×10-13,
obtained from hydrogenic Lamb shifts [8].
c)≈1.0×10-13,
obtained from hydrogenic Lamb shifts [8].
Tachyonic radiation implies superluminal signal transfer, the energy quanta propagating faster than light in vacuum, due to their negative mass-square, in contrast to rotating superluminal light sources emitting vacuum Cherenkov radiation [9], [10], [11], [12], [13] and [14]. This superluminal energy propagation by tachyonic vacuum modes is also to be distinguished from superluminal group velocities arising in photonic crystals, optical fibers, or metamaterials [15], [16], [17], [18] and [19]. In contrast to tachyonic quanta, the actual signal speed defined by the electromagnetic energy flow in these media is always subluminal and occasionally even opposite to the group velocity [20].
In Section 2, we derive the fugacity expansion of the internal energy and the partition function in the low-temperature/high-density regime. The thermodynamic variables of nearly degenerate power-law distributions are calculated in Section 3, such as the thermal equation of state, entropy, and free energy. We check the positivity of the isochoric heat capacity and the isothermal compressibility for arbitrary power-law index, demonstrating thermodynamic stability in the quantum regime. A generalization of non-relativistic Fermi–Dirac distributions by way of modified dispersion relations has also been suggested in Ref. [21]. Here, we consider ultra-relativistic multi-component plasmas in the collisionless regime [22], in stationary non-equilibrium described by power-law densities [1], [23] and [24].
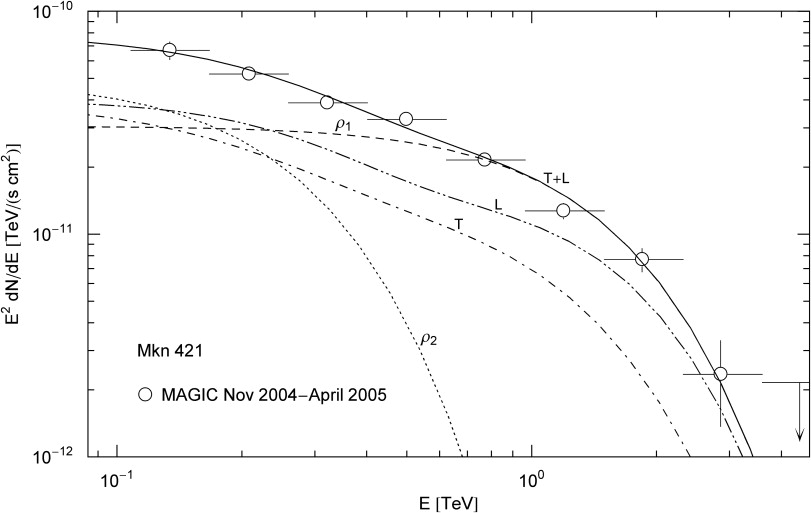
In Section 4, we study tachyonic radiation densities averaged over electronic power-law distributions, calculate the spectral functions in the nearly degenerate quantum regime, and discuss the range of applicability of the fugacity expansion, including the crossover into the quasiclassical regime. We perform cascade fits to the γ-ray flux of the Markarian galaxy Mkn 421 (at redshift z≈0.031) in a quiescent state [25] and to a burst spectrum [26], and compare with the tachyonic spectral maps of other BL Lacertae objects. The spectral curvature is reproduced by the tachyonic cascades without resort to intergalactic attenuation mechanisms.
In Section 5, we present our conclusions. In Appendix A, the Sommerfeld asymptotics of incomplete Fermi integrals is derived, which is the basis of the fugacity expansion of the thermodynamic functions in Section 3 and the spectral functions in Section 4. This involves polylogarithms discussed in Appendix B.
2. Ultra-relativistic Fermi power laws
We start with the partition function
where the electronic Lorentz factors range in an interval γ1≤γ<∞. γ1 is the lower edge of Lorentz factors of the electron distribution, the threshold energy being mγ1, γ1≥1. The fugacity exponent α is related to the chemical potential by μ=-mα/β. δ is the electronic power-law exponent, and β=m/(kT) the cutoff parameter in the Boltzmann factor, so that the Fermi–Dirac equilibrium distribution is recovered with δ=0 and γ1=1. Here, we study non-thermal power-law ensembles of arbitrary real power-law index δ. The grand partition function (2.1) is obtained via a standard trace calculation in fermionic occupation number representation. Internal energy and particle number read
Integral representation (2.1) of the partition function Z(δ,β,α,V) is the starting point for the quasiclassical fugacity expansion of the thermodynamic functions, applicable at high temperature and low density [27]. The opposite asymptotic limit, the nearly degenerate quantum regime at low temperature and high density, is based on the representation
obtained from Eq. (2.1) by partial integration. We replace α by the chemical potential μ=-mα/β, and consider U, N, and
The μ→∞
asymptotics of the above variables is assembled from the fugacity
expansion of the Fermi integrals in Appendix A. The
ascending 1/μ series of the particle number reads,
cf. Eqs. (A.35) and (A.37),
and the expansion of the partition function follows from Eq. (A.38):
For these asymptotics to be applicable, conditions m/μ
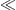 1 and m/(βμ)
1 and m/(βμ) 1 have to be met. The identities
1 have to be met. The identitiescan be used to check the consistency of series expansions (2.6), (2.7) and (2.8).
3. Thermodynamic variables of nearly degenerate power-law distributions
The thermodynamic functions are obtained by iteratively
solving (2.6) for the
chemical potential μ, which is then substituted
into the asymptotic series (2.7) and (2.8) of the
internal energy and the partition function. Defining the Fermi momentum
as pF:=(3π2N/V)1/3,
we invert Eq. (2.6) in
ascending powers of 1/pF:
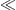 1 and x
1 and x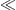 1. The Fermi temperature is defined as
the β→∞
limit of μ(pF,β):
1. The Fermi temperature is defined as
the β→∞
limit of μ(pF,β):We substitute μ(pF,β) into the internal energy (2.7) and partition function (2.8) to find
The mean energy per particle in the ultra-relativistic regime is thus U/N
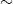 3pF/4.
The entropy is calculated via
3pF/4.
The entropy is calculated viawhere we used
The expansion parameter is x=m/(βpF) or
The isochoric heat capacity reads
Thermodynamic stability requires CV≥0, which is evidently satisfied. The Helmholtz free energy is assembled as
where we substitute the fugacity expansions of the chemical potential (3.1) and the partition function (3.4) as well as
with x=m/(βpF) as in Eq. (3.7). The thermal equation of state
is thus found as
We solve this equation iteratively for pF(β,P):
where y:=(12π2P)1/4. The thermal equation (3.12) can thus be written as
These expansions in ascending powers of 1/y are applicable if m/y
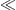 1 as well as m/(βy)
1 as well as m/(βy)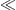 1. The isothermal compressibility reads
1. The isothermal compressibility readswhere, cf. Eq. (3.13),
so that we arrive at
with y=(12π2P)1/4. Thermodynamic stability requires κT≥0, which is satisfied.
In the fully degenerate case, at zero temperature, the
power-law exponent δ drops out in all thermodynamic
variables, and at finite β it does not enter in
leading order. The regime below βF:=m/(kTF)
is not accessible with the fugacity expansions derived here, which
require both βF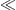 1 and βF/β
1 and βF/β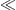 1. If β
1. If β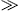 1/βF,
the first-order correction proportional to δ is
overpowered by the second order, which is independent of δ
in this limit. Therefore, the Chandrasekhar mass limit of white dwarfs
is not affected by the power-law exponent, as it assumes total
degeneracy [28].
Order-of-magnitude estimates of cooling times derived from homology
relations are not affected either, as they are based on the
leading-order temperature and density scaling of pressure and specific
heat [29].
1/βF,
the first-order correction proportional to δ is
overpowered by the second order, which is independent of δ
in this limit. Therefore, the Chandrasekhar mass limit of white dwarfs
is not affected by the power-law exponent, as it assumes total
degeneracy [28].
Order-of-magnitude estimates of cooling times derived from homology
relations are not affected either, as they are based on the
leading-order temperature and density scaling of pressure and specific
heat [29].
We have put 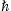 =c=1.
To restore the dimensions, we rescale β=mc2/(kT)
and pF=
=c=1.
To restore the dimensions, we rescale β=mc2/(kT)
and pF=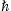 (3π2N/V)1/3
so that kTF
(3π2N/V)1/3
so that kTF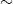 μ
μ cpF,
and note
cpF,
and note ![]() .
The expansion parameter x=mc/(βpF)
is chosen to be dimensionless, and the dimension of y=(12π2
.
The expansion parameter x=mc/(βpF)
is chosen to be dimensionless, and the dimension of y=(12π2 3c3P)1/4
to be that of energy. The expansion parameter mc2/y
in Eq. (3.13) is thus
dimensionless as well, and pF
3c3P)1/4
to be that of energy. The expansion parameter mc2/y
in Eq. (3.13) is thus
dimensionless as well, and pF y/c.
Hence
y/c.
Hence
4. Tachyonic cascade spectra
The spectral averaging of tachyonic radiation densities with
electronic power-law distributions (2.2) has
already been explained in Ref. [30], where we
mainly focused on the quasiclassical regime, but also derived the
general formalism applicable in the nearly degenerate case. In Eqs. (4.1), (4.2), (4.3), (4.4) and (4.5), we
summarize the averaged radiation densities:
The weight factors fk=1,2,3 denote the averages
where AF:=m3V/π2 is the normalization factor of the power-law density dρF in Eq. (2.2). The superscripts T and L in Eq. (4.2) refer to the transversal and longitudinal polarization components defined by
The threshold Lorentz factor γ1 enters as lower integration boundary in the weights (4.3), and γ1≥μt. In the thermodynamic variables, we can still put γ1=1, cf. Eqs. (2.3), (2.4) and (2.5), but electrons with Lorentz factors below μt cannot radiate tachyonic quanta [32]. γ1 determines the break frequency
which enters in the step functions θ in Eq. (4.1), separating the spectrum into a low- and a high-frequency band. In particular,
The units  =c=1
can easily be restored. We use the Heaviside–Lorentz system, so that αq=q2/(4π
=c=1
can easily be restored. We use the Heaviside–Lorentz system, so that αq=q2/(4π c)≈1.0×10-13.
The tachyon mass is
c)≈1.0×10-13.
The tachyon mass is ![]() ,
and the tachyon–electron mass ratio mt/m≈1/238.
These estimates are obtained from hydrogenic Lamb shifts [8]. The
particle number reads
,
and the tachyon–electron mass ratio mt/m≈1/238.
These estimates are obtained from hydrogenic Lamb shifts [8]. The
particle number reads ![]() ,
where γ1
is the lower edge of Lorentz factors in the source population. The
exponential cutoff in the spectral weights (4.3) is related
to the electron temperature by β=mc2/(kT)
and the chemical potential by μ=-mα/β.
The normalization factor AF
is dimensionless via m→mc/
,
where γ1
is the lower edge of Lorentz factors in the source population. The
exponential cutoff in the spectral weights (4.3) is related
to the electron temperature by β=mc2/(kT)
and the chemical potential by μ=-mα/β.
The normalization factor AF
is dimensionless via m→mc/ ;
the volume factor in the thermodynamic functions in Section 3 is
thus found as
;
the volume factor in the thermodynamic functions in Section 3 is
thus found as ![]() ,
where
,
where ![]() is the reduced electronic Compton wavelength.
is the reduced electronic Compton wavelength.
The weight factors (4.3) are
related to the Fermi integral F(a,
b) in Eq. (A.1) (with a=k-1
and b=0) and the Sommerfeld decomposition (A.3) by
The expansion parameter z is defined in Eq. (A.20):
where μ is the chemical potential, cf. after Eq. (4.5). For the asymptotic series (4.7) to be applicable, conditions βγ1z
 1
as well as z>1
have to be satisfied. [Since b=0, we do not need to
require γ1z
1
as well as z>1
have to be satisfied. [Since b=0, we do not need to
require γ1z 1,
even though series (4.7) is a
systematic ascending 1/z expansion, cf. Eq. (A.23) and after
Eq. (A.34). In fact,
F0
is a polynomial in z, and the factor ρ(γ1z)
in Eq. (A.21) drops out
in F1+F2
at b=0, cf. Eqs. (A.13) and (A.15), so that
an additional temperature independent expansion in inverse powers of γ1z
is not needed if b=0 in the Fermi integral (A.1).]
1,
even though series (4.7) is a
systematic ascending 1/z expansion, cf. Eq. (A.23) and after
Eq. (A.34). In fact,
F0
is a polynomial in z, and the factor ρ(γ1z)
in Eq. (A.21) drops out
in F1+F2
at b=0, cf. Eqs. (A.13) and (A.15), so that
an additional temperature independent expansion in inverse powers of γ1z
is not needed if b=0 in the Fermi integral (A.1).]
The amplitude AF
and the fugacity e-α
are two independent fitting parameters in the source density dρF(γ),
cf. Eqs. (2.2) and (4.3). This is
in contrast to the classical limit, ![]() ,
where the factors of the amplitude AFe-α
cannot independently be determined from the spectral fit. This
amplitude differs from a classical Boltzmann power-law distribution due
to the fermionic multiplicity factor, the Boltzmann normalization being
AFe-α/2,
cf. Eq. (3.7) in Ref. [24]. In the
ultra-relativistic limit, γ
,
where the factors of the amplitude AFe-α
cannot independently be determined from the spectral fit. This
amplitude differs from a classical Boltzmann power-law distribution due
to the fermionic multiplicity factor, the Boltzmann normalization being
AFe-α/2,
cf. Eq. (3.7) in Ref. [24]. In the
ultra-relativistic limit, γ 1,
the factor γ-δ
can formally be generated by analytic continuation in the momentum
space dimension, since p
1,
the factor γ-δ
can formally be generated by analytic continuation in the momentum
space dimension, since p mγ
[33]. In the
case of a genuine fermionic power-law distribution in the nearly
degenerate quantum regime, one can determine the volume as well as the
particle number from the spectral fit, cf. after Eq. (4.5).
mγ
[33]. In the
case of a genuine fermionic power-law distribution in the nearly
degenerate quantum regime, one can determine the volume as well as the
particle number from the spectral fit, cf. after Eq. (4.5).
We parametrize the spectral weights fk(γ1)
with the chemical potential via z(μ)
in Eq. (4.8). The
independent fitting parameters in fk(γ1)
are thus temperature β, threshold Lorentz factor γ1,
chemical potential μ, and the volume factor AF
of the Fermi distribution in Eq. (4.3). We may
fix γ1
at the lowest possible threshold, γ1=μt,
cf. Eq. (4.4) (and put γ1=1
in the thermodynamic functions (2.3), (2.4) and (2.5)), so that
the averaged spectral densities (4.1) simplify to
 1
is not met, the asymptotic series of F1+F2
in Eq. (4.7) breaks
down, so that we have to switch to the exact integral representation (4.3) of the
weight factors fk(γ1),
and numerically integrate the crossover into the quasiclassical regime.
The quasiclassical fugacity expansion [2] can be used
if
1
is not met, the asymptotic series of F1+F2
in Eq. (4.7) breaks
down, so that we have to switch to the exact integral representation (4.3) of the
weight factors fk(γ1),
and numerically integrate the crossover into the quasiclassical regime.
The quasiclassical fugacity expansion [2] can be used
ifwhich allows to expand the denominator in Eq. (2.2) to arrive in leading order at the classical power-law density, cf. after Eq. (4.8),
Here, we use the customary definition of the electronic power-law index,
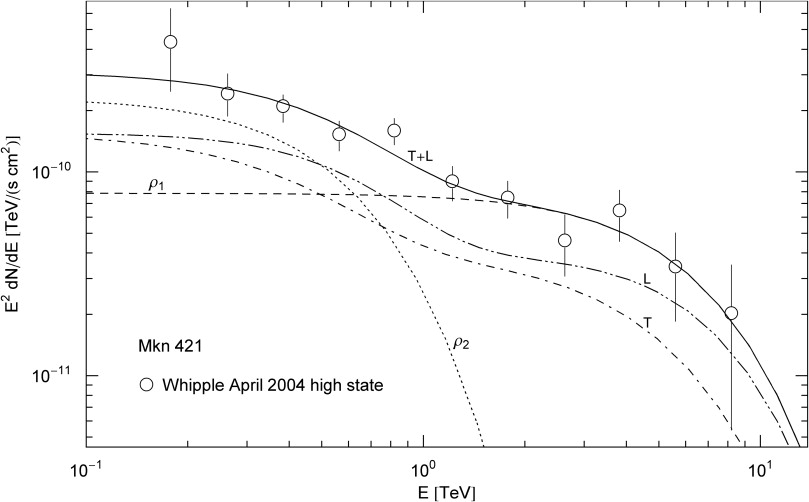
Thermal electronic source distributions ρi generating the tachyonic γ-ray cascades of the Markarian galaxy Mkn 421.
Each ρi
stands for a Maxwell–Boltzmann density ![]() as defined in Eq. (4.11) (with δ=0
and γ1=1).
β is the cutoff parameter in the Boltzmann factor,
and
as defined in Eq. (4.11) (with δ=0
and γ1=1).
β is the cutoff parameter in the Boltzmann factor,
and ![]() determines the amplitude of the tachyon flux generated by density ρi,
from which the electron count
determines the amplitude of the tachyon flux generated by density ρi,
from which the electron count ![]() is inferred at the indicated distance. kT
is the temperature and U
the internal energy of the electron populations, cf. after Eq. (4.15). Each
cascade depends on two fitting parameters β and
is inferred at the indicated distance. kT
is the temperature and U
the internal energy of the electron populations, cf. after Eq. (4.15). Each
cascade depends on two fitting parameters β and ![]() extracted from the χ2
fit T+L=ρ1+ρ2
in Fig. 1 and Fig. 2. The
tachyonic cascades labeled ρ1,2
in the figures are produced by the corresponding electron densities
listed in this table.
extracted from the χ2
fit T+L=ρ1+ρ2
in Fig. 1 and Fig. 2. The
tachyonic cascades labeled ρ1,2
in the figures are produced by the corresponding electron densities
listed in this table.
The classical limit of the fermionic spectral functions FT,L(ω,γ1)
is the Boltzmann average BT,L(ω,γ1),
obtained by dropping all terms containing mt/m
factors in Eq. (4.2), and
replacing dρF
in the spectral weights (4.3) by the
classical density ![]() in Eq. (4.11). The
classical spectral weights reduce to incomplete gamma functions. Terms
containing mt/m
factors in Eqs. (4.4) and (4.5) are
dropped as well, and the polarization coefficients reduce to
in Eq. (4.11). The
classical spectral weights reduce to incomplete gamma functions. Terms
containing mt/m
factors in Eqs. (4.4) and (4.5) are
dropped as well, and the polarization coefficients reduce to ![]() and
and ![]() ,
cf. after Eq. (4.3). The
classical limit of the averaged spectral densities
,
cf. after Eq. (4.3). The
classical limit of the averaged spectral densities  pT,L(ω)
pT,L(ω) F
in Eq. (4.1) thus reads
F
in Eq. (4.1) thus reads
where the argument
The spectral fits of the BL Lacertae object (BL Lac) Markarian
421 in Fig. 1 and Fig. 2 are based
on the E2-rescaled
flux densities [34]
we use a rescaled parameter
which is independent of the distance estimate in Eq. (4.13). Here,
 cz/H0,
with
cz/H0,
with Fig. 1 shows the cascade fit of the Markarian galaxy Mkn 421 in a quiescent state [25], and Fig. 2 in a high emission state [26]. The redshift of Mkn 421 is z≈0.031, implying a distance of 140 Mpc. TeV γ-ray spectra of active galactic nuclei are usually assumed to be generated by inverse Compton scattering or pp scattering followed by pion decay. Both mechanisms result in a flux of TeV photons, assumed to be partially absorbed by interaction with background photons due to pair creation, so that the intrinsic spectrum has to be reconstructed on the basis of intergalactic absorption models depending on vaguely known cosmological input parameters. In contrast, the extragalactic tachyon flux is not attenuated by interaction with the background light, there is no absorption of tachyonic γ-rays. The curvature of the γ-ray spectra in double-logarithmic plots is caused by the Boltzmann factor of the electron densities generating the tachyon flux, so that the observed spectrum is already the intrinsic one, and no reconstruction is needed. The curvature present in the γ-ray spectra of BL Lacs is not correlated with distance; the spectral curvature does not increase with redshift if we compare the spectral fits in Fig. 1 and Fig. 2 to the spectral maps of other active galactic nuclei, cf. the figure captions.
5. Conclusion
Tachyonic γ-ray spectra of active galactic nuclei are generated by ultra-relativistic electron populations. Tachyons are radiation modes, unrelated to electromagnetic radiation. Electrons radiate tachyons, and these tachyonic quanta produce the observed γ-ray cascades. The tachyonic radiation modes are coupled by minimal substitution to the electron current. This field theory, a real Proca field with negative mass-square, admits a static potential analogous to the Coulomb potential, but oscillating because of the negative mass-square, and much weaker due to the small tachyonic fine structure constant. In the spectral maps, the tachyon–electron mass ratio shows in the cutoff energy of the cascades. The negative mass-square of tachyons implies superluminal velocity and allows longitudinal polarization. The tachyonic radiation field does not couple to electromagnetic fields, nor is it affected by electric charge. Thus, interaction of tachyons with photons can only happen indirectly via matter fields. In contrast to electromagnetic γ-rays, there is no extinction of the extragalactic tachyon flux by the cosmic background light, as tachyons do not interact with infrared photons. The ultra-relativistic electron plasma in the active galactic nucleus produces tachyonic γ-rays propagating unattenuated over intergalactic distances.
The tachyonic radiation density averaged over the electron populations in the galactic nucleus is generated by electrons in uniform motion. In particular, there is no electromagnetic radiation damping, as photons can only be radiated by accelerated charges, in contrast to tachyonic quanta, where the emission rate primarily depends on the electronic Lorentz factor rather than on acceleration [3]. The high plasma temperature inferred from the spectral fits implies ultra-high energy electrons. Such high electron temperatures are also found in Galactic pulsar wind nebulae, production sites of ultra-high energy cosmic rays [36].
Specifically, we fitted a quiescent as well as a flare spectrum of the γ-ray blazar Mkn 421 with tachyonic cascades, and found that the spectral curvature is intrinsic and reproduced by the superluminal spectral densities (4.1) averaged with ultra-relativistic electron distributions. The curvature present in the γ-ray spectra of active galactic nuclei is not correlated with distance, so that absorption of electromagnetic radiation due to interaction with background photons is not a viable explanation for the spectral curvature. By contrast, there is no intergalactic attenuation of the tachyon flux, as tachyons cannot interact with photons. In Table 1, we have given estimates of the temperature, the source count, and the internal energy of the electron populations in the galactic nucleus generating the superluminal γ-ray cascades.
The fugacity expansion of the thermodynamic variables of a nearly degenerate electron plasma was derived in Sections 2 and 3, and fermionic power-law densities were shown to admit a stable and extensive entropy function in the quantum regime, cf. Eqs. (3.5) and (3.6). In Section 4, we averaged tachyonic spectral densities with electronic power-law distributions, and obtained the fugacity expansion of the quantized spectral functions in the nearly degenerate low-temperature/low-frequency/high-density regime. The integral representation (4.3) of the spectral weights covers the crossover into the quasiclassical high-temperature/high-frequency/low-density regime studied in Ref. [2].
Superluminal radiation from ultra-relativistic electrons orbiting in magnetic fields was investigated in Ref. [37]. In the zero-magnetic-field limit, the averaged tachyonic synchrotron densities converge to the spectral densities (4.12). Orbital curvature induces modulations in the spectral slopes, but these ripples are attenuated when performing a pitch-angle average, cf. Figs. 1–3 of Ref. [37]. Thus we can use uniform radiation densities even in the presence of magnetic fields in the galactic nuclei.
Acknowledgments
The author acknowledges the support of the Japan Society for the Promotion of Science. The hospitality and stimulating atmosphere of the Centre for Nonlinear Dynamics, Bharathidasan University, Trichy, and the Institute of Mathematical Sciences, Chennai, are likewise gratefully acknowledged.
References
Appendix A. Incomplete integrals of fermionic power-law densities
The thermodynamic variables in Eqs. (2.3), (2.4) and (2.5) are
composed of integrals of type
We perform the substitution γ=γ1(1+y)
in Eq. (A.1),
and use the Sommerfeld decomposition [39]:
The asymptotics of the temperature-dependent contribution F1+F2 is discussed below, and the zero-temperature degeneracy F0 in Section A.2.
A.1. Fugacity expansion at low temperature and high density
The ascending ![]() expansion of F1+F2
in Eq. (A.3) is found
by means of the substitutions y=λ(1-t)
in F1
and y=λ(1+t)
in F2.
Expanding the denominator in powers of
expansion of F1+F2
in Eq. (A.3) is found
by means of the substitutions y=λ(1-t)
in F1
and y=λ(1+t)
in F2.
Expanding the denominator in powers of ![]() ,
we obtain
,
we obtain
where f(y) is defined in Eq. (A.2). In F1, we extend the upper integration boundary to infinity, which is justified by Watson's lemma, as the error is of order O(1/Λ), as compared to the expansion in powers of
and does not depend on the upper integration boundary if terms of O(1/Λ) are neglected [40]. For technical convenience, we extend the integration boundaries to infinity, even though series (A.7) may only have a small radius of convergence, cf. Eq. (B.17). (In this way, we avoid incomplete gamma functions in the term-by-term integrations in Eqs. (A.4) and (A.5), which would have to be expanded to arrive at series (A.8) and (A.9) below.) On substituting series (A.7) into Eqs. (A.4) and (A.5), and interchanging integration and summations, we find
To obtain the Taylor coefficients ak,n(δ,λ) in Eq. (A.7), we factorize gk(t,δ,λ)=h1h2, cf. Eqs. (A.2) and (A.6),
and expand both factors. The Taylor series of h1 reads
As for h2, we introduce the shortcuts
and find, by means of the Gegenbauer expansion (B.17):
We replace the binomial coefficient (kδ+a)m/m! in Eq. (A.11) by the Stirling expansion (B.14), and use the product of series (A.11) and (A.13) to find the Taylor coefficients of gk(t,δ,λ) in Eq. (A.7) as
The coefficients S(n,m;a) are calculated in Eqs. (B.15) and (B.16), and we put αn,m(λ)=0 for m>n. The Gegenbauer polynomials
The expansion of F2 is obtained from F1 by changing the sign of δ and inserting the factor (-1)n+1 into the n summation. The expansion of F1+F2 is thus
where Δn are polynomials in
The first three orders of the asymptotic expansion of F1+F2 in Eq. (A.17) thus read
where Δk=1,2,3 stands for Δk((1+λ)δ), cf. Eqs. (B.11) and (B.12), and ρ is defined in Eq. (A.12). We introduce z=1+λ as expansion parameter (in ascending powers of 1/z):
where Λ0 is the fugacity, cf. Eq. (A.1), and
We also note, cf. Eq. (B.12),
Expansion (A.19) is in ascending powers of 1/(βγ1z), and holds for arbitrary exponents a,b, and γ1≥1, provided that βγ1z
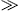 1.
If in addition γ1z
1.
If in addition γ1z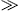 1,
we can also expand ρ in Eq. (A.21) to find
1,
we can also expand ρ in Eq. (A.21) to findFor this expansion to be valid, βγ1z
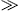 1
as well as γ1z
1
as well as γ1z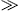 1
is required. That is, both conditions have to be met in a systematic 1/z
expansion, where z is related to the fugacity Λ0=e-α
as stated in Eq. (A.20).
1
is required. That is, both conditions have to be met in a systematic 1/z
expansion, where z is related to the fugacity Λ0=e-α
as stated in Eq. (A.20).
A.2. Zero-temperature degeneracy
In the zero-temperature limit, the contribution F1+F2
to the Fermi integral F(a,b)
in Eq. (A.1) vanishes,
cf. Eqs. (A.19) and (A.23), so that F
reduces to the temperature-independent residual ![]() ,
cf. Eq. (A.3). We
substitute
,
cf. Eq. (A.3). We
substitute ![]() into F0
in Eq. (A.3), and
rescale t to find
into F0
in Eq. (A.3), and
rescale t to find
We consider the limit λ→∞, and expand F0 in ascending powers of
In the integrand of
where (a)n denotes the falling factorial, a(a-1)…(a-n+1). The ascending
We consider the special case γ1=1,
that is υ1=0
in Eq. (A.24). Here, b>-2
is necessary for integral (A.24) to
converge,
where ψ is the logarithmic derivative of the gamma function. The asymptotic expansion of the Fermi integral
We list the integrals F0(a,b)
(defined in Eq. (A.24))
occurring in the thermodynamic functions (2.3), (2.4) and (2.5). As in Eq.
(A.20), we put z=1+λ,
so that ![]() ,
cf. Eq. (A.25), and
obtain by elementary integration of Eq. (A.24),
,
cf. Eq. (A.25), and
obtain by elementary integration of Eq. (A.24),
where 0<arcsin<π/2, z>1, and γ1≥1. The partition function (2.5) is assembled from
and there is also a zero-temperature contribution from F1+F2 via βF(0,3), cf. Eq. (A.38). The spectral functions (4.10) are compiled at b=0, where
which is independent of γ1, cf. Eq. (A.24).
We consider γ1=1
and expand Eqs. (A.31) and (A.32) in 1/z
to find
Here, γ1=1 is implied, but γ1 can readily be scaled into these series according to Eqs. (A.31) and (A.32), so that the expansions are in ascending powers of 1/(γ1z). Eqs. (A.31), (A.32) and (A.33) give the fully degenerate contribution F0(a,b) to the Fermi integral (A.1), (A.2) and (A.3). The fugacity expansion (A.34) of F0 is needed even though the exact result (A.31) and (A.32) is known, since we have to iteratively solve for z when calculating the thermodynamic variables, cf. Section 3.
A.3. Number count, internal energy, and partition function in the nearly degenerate regime
The fugacity expansion of the Fermi integral F(a,b,γ1=1)
in Eq. (A.1) is
obtained by adding F1+F2
in Eq. (A.23) (with γ1=1)
and F0
in Eq. (A.34). We find,
for exponents a=b=1:
with b=1. The latter is also the expansion of F(0,3), if we put b=3 in the third and fourth term. The ellipses in Eqs. (A.35) and (A.36) stand for terms of
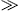 1.
The parameter Λ0
in Eq. (A.1) is
identified with the fugacity e-α,
which is related to the chemical potential by α=-βμ/m,
where β=m/(kT).
Hence, if γ1=1,
we can identify z=μ/m,
cf. Eq. (A.20).
1.
The parameter Λ0
in Eq. (A.1) is
identified with the fugacity e-α,
which is related to the chemical potential by α=-βμ/m,
where β=m/(kT).
Hence, if γ1=1,
we can identify z=μ/m,
cf. Eq. (A.20).
The fugacity expansions of the particle number and the
internal energy read, cf. Eqs. (2.3), (2.4) and (A.1),
Here, F(0,3) is series (A.36), and F(-1,3) series (A.35), both with b=3. The ellipsis stands for terms of
Appendix B. Polylogarithms, Stirling numbers, and Gegenbauer polynomials
To keep this article self-contained, we summarize some
technical concepts as well as the notation used in the expansion of the
Fermi integrals in Appendix A. We
start with the series representation of the polylogarithm [40], [41], [42], [43], [44], [45], [46] and [47]:
The first integral converges in the half-plane Re(s)>1, the second and third require Re(s)>0; otherwise they are identical via partial integration and obvious substitutions. Series (B.1) is recovered by expansion in ascending powers and term-by-term integration. Fermi–Dirac integrals are defined by the third representation in Eq. (B.2), as -Γ(s)Lis(-z).
We note Lis(-1)=(21-s-1)ζ(s);
in particular, ![]() and Li2(-1)=-π2/12.
We will mainly consider real negative z or at least
z<1.
Lis(z)
is analytic in the z plane with branch cut (1,∞)
along the positive real axis, except for s=0
and at negative integer s, where the polylogs are
rational functions, obtained by recursive differentiation of Li1(z)=-log(1-z)
according to
and Li2(-1)=-π2/12.
We will mainly consider real negative z or at least
z<1.
Lis(z)
is analytic in the z plane with branch cut (1,∞)
along the positive real axis, except for s=0
and at negative integer s, where the polylogs are
rational functions, obtained by recursive differentiation of Li1(z)=-log(1-z)
according to
where
is the Hurwitz zeta function, and r>0 is implied in Eq. (B.4). ζ(s,z) admits the integral representation [48]:
from which the large-z asymptotics is obtained by substituting the generating series of the Bernoulli numbers:
and using term-by-term integration (which amounts to applying Fourier asymptotics or Watson's lemma if the integration path is rotated into the imaginary axis [40]). The r→∞ asymptotics of the inversion formula (B.4) is thus found as [47]:
where
Here, (s)n is the falling factorial s(s-1)…(s-n+1), not to be confused with the Pochhammer symbol or rising factorial (s)(n):=s(s+1)…(s+n-1), so that (s)n=(-1)n(-s)(n).
The second polylog on the left-hand side of Eq. (B.8) can be
dropped, eiπsLis(-1/r)=O(1/r),
as terms of this order have been discarded in the expansion procedure.
However, the asymptotic series terminates for integer s≥0,
and then Eq. (B.8) holds true
as an identity even for small r. In the case of
negative integer s, the right-hand side of Eq. (B.8) vanishes
due to the poles of Γ(1+s)
in the denominator. In Eq. (B.8), we put s=n=0,1,2,…
to find [42]
Apparently Δn(1/r)=(-1)nΔn(r). Finally, multiple s differentiation of Γ(s)Lis(z) amounts to adding a factor of
In Appendix A, we
also need the polynomial expansion of the falling factorial:
where k, δ, and a are arbitrary real numbers. In particular, S(n,m;0)=Sn,m/n!, and we define S(n,m;a)=0 if m>n. For n=0,1,2, coefficients (B.15) read
In Eq. (A.13), we use an expansion in Gegenbauer polynomials, based on the generating series [48]:
Splitting the left-hand side into two factors (1-t/ρ±)α,
where (λ)(n) is the Pochhammer symbol Γ(λ+n)/Γ(λ). We note
Gegenbauer polynomials are a special class of hypergeometric polynomials,
At λ=1/2, they coincide with the Legendre polynomials Pn(x), and at λ=1 with the Chebyshev polynomials of the second kind Un(x) [48]. Finally,