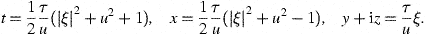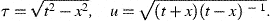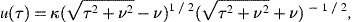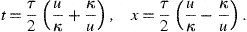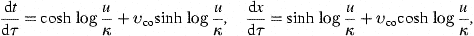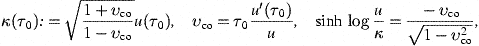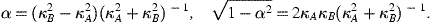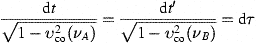Abstract

The relativistic time dilation is reviewed in a cosmological context. We show that a clock or twin paradox does not arise if cosmic time is properly taken into account. The receding galaxy background provides a unique frame of reference, and the proper times of geodesic as well as accelerated observers can be linked to the universal cosmic time parameter. This suggests to compare the proper time differentials of the respective observers by determining their state of motion in the galaxy grid. In this way, each observer can figure out whether his proper time is dilated or contracted relative to any other. In particular one can come to unambiguous conclusions on the aging of uniformly moving observers, without reference to asymmetries in measurement procedures or accelerations they may have undergone.

1. Introduction

The clock paradox admits, quite in the framework of special relativity, a simple and consistent solution [1]: There is always an asymmetry concerning the rest frames of the observers involved, usually one of them is at some point accelerated, and the other derives from an infinitesimal Lorentz boost the time dilation , where υ(t) is the speed of the accelerated observer measured in the inertial frame, and t^′ and t are the proper times of the accelerated and the inertial observer, respectively, so that a clock in the accelerated frame is lagging behind. One may now wonder why this has provoked relentless discussion. Someone in motion ages less than someone at rest, this may be surprising, but is not really paradoxical. The paradox arises because rest and uniform motion are equivalent in relativity theory, and if both observers are uniformly moving most of the time, it is just hard to digest that a short and tiny acceleration can make the difference, can decide on who stays young and who grows old. Hence, in a relativistic space–time conception, this paradox stays paradoxical, despite its logical solution. Hafele and Keating, in their discussion of correction terms pertinent to their around-the-world atomic clocks experiment [2] and [3], spot an ‘objective physical relationship of inertial systems with the universe’, hinting at the natural resolution of the paradox. However, adopting a relativistic worldview, they do not succeed in specifying. Otherwise their conclusions are beyond any doubt, a high-precision test of the time dilation in the ultra-relativistic regime is provided by muon lifetime measurements in g−2 experiments [4], [5], [6] and [7]. Here, we will quantify the relationship between inertial frames and the universe, and analyze the time dilation in the cosmic space–time defined by the expanding galaxy grid, where rest and uniform motion become distinguishable states [8] and [9]. The proper time of each observer can be linked to the universal cosmic time defined by the receding galaxy background, which allows an unambiguous mutual comparison of their proper time differentials. However, the observer’s proper time and age are not determined relative to a counterpart, a twin or so, but rather by his proper movement in the galaxy grid. This is the crucial difference to the relativistic interpretation of the time dilation, which leads to a clock paradox due to the symmetry of the relative velocity.

2. Synchronization of cosmic and local time

We study a linearly expanding Robertson–Walker cosmology with negatively curved 3-space [10] and [11]; this cosmology admits globally geodesic rest frames for uniformly moving observers synchronized by Lorentz boosts, otherwise the reasoning is not bound to a specific expansion factor (cf. the remark at the end of this section). We use ds²=−dτ²+τ²u⁻²(du²+|dξ|²) as line-element in comoving coordinates, where (u,ξ) denote Cartesian coordinates in the Poincaré half-space H³, so that u>0 and ξ=x₁+ix₂ (cf. [12]). Cosmic time τ ranges in 0<τ<∞. This 4-manifold can be isometrically mapped onto the interior of the forward light cone, t²−x²>0, t>0, ds²=−dt²+dx², via

We consider geodesic motion along the u-semiaxis of H³, and put dξ=0 and dy=dz=0 in the line-elements, as well as ξ=0 in (1), so that comoving and geodesic coordinates connect by

The geodesic rest frames of uniformly moving observers can be synchronized by a boost

corresponding to a scale transformation in comoving coordinates,


and inversely, α=(η²−1)(η²+1)⁻¹. The worldlines of geodesic observers read [13],

where κ>0 and ν are integration constants, the latter determining their velocity in the comoving galaxy frame,

Galactic observers are defined by constant space coordinates (ν=0) in this comoving (τ,u)-frame. The trajectories (5) are mapped into the forward light cone (x-axis) by (2); in this geodesic (t,x)-frame, we find the worldlines

The time parameter t in (7) ranges in the interval [|ν|κ^−sign(ν),∞], which corresponds via (2) to the τ-interval [0,∞]. In geodesic coordinates, the worldline of a galactic observer u=κ reads x=υ(κ)t (cf. (7)) and we can introduce the forward light cone as rest frame by applying (2) and a subsequent boost (3) with α=(κ²−1)(κ²+1)⁻¹, so that his worldline is just x^′=0 in his rest frame t^′2−x^′2>0, t^′>0. The same can be effected by a rescaling u→κ⁻¹u in (2), and thus we obtain the geodesic rest frame (t,x) of a galactic (κ,ν=0) or uniformly moving (κ,ν≠0) observer (5) by means of the transformation

The geodesic rest frame of a uniformly moving observer (κ,ν) is accordingly a truncated copy of the forward light cone, t²−x²>0, t>|ν|. The galaxies radially emanate from x=0, and since he is located at x=−ν (cf. (7)) the galactic recession appears anisotropic, so that he can infer his velocity (6) and his trajectory (5) in the comoving galaxy frame. (This frame is determined up to a H³-isometry such as (4).) The state of rest, defined by galactic observers, and uniform motion become easily distinguishable. In an expanding universe, the distinction of uniform motion and rest is not only possible but unavoidable, because the galaxy background cannot be ignored. The mentioned anisotropy can be visualized by a chain u=κ_n of galaxies, say, κ_n=be^na, a,b>0, nZ, aligned along the u-semiaxis, in this case equidistantly according to the 3-space metric d(κ_m,κ_n)=τ|log(κ_m/κ_n)|. In the geodesic rest frame of observer (κ,ν), these galaxies emerge as x=υ_nt, with υ_n:=(κ_n²−κ²)(κ_n²+κ²)⁻¹ and t>|ν|.

In the geodesic rest frame (8) we find, for galactic, uniformly moving and accelerated observers u(τ) alike, the cosmic time derivatives

where υ_co:=τu^′/u. The observer’s trajectory u(τ) is subjected to |υ_co|<1, but otherwise arbitrary. His velocity in the geodesic frame is dx/dt, parametrized by cosmic time via (9). In the case of uniformly moving (or galactic) observers (5), we may write the differentials (9) as and dx=0, with υ_co in (6), according to x=−ν and , so that t dt=τ dτ and υ_co=ν/t. The proper time of accelerated observers is likewise readily identified. At a given instant τ₀ of cosmic time, we choose in (9)

so that the differentials again reduce to and dx=0, with υ_co defined in (10). In the geodesic rest frame (x,t) of a galaxy κ(τ₀) (cf. (8)) we thus find the coordinates of the (accelerated) observer u(τ₀) as

The geodesic frames κ(τ₀) do not depend on τ₀ if the observer is uniformly moving, and then Eq. (11) reduces to x=−ν, so that (t,x) are geodesic coordinates for this observer. The proper time of an accelerated observer is found by means of a sequence of geodesic galaxy frames κ(τ), chosen in a way that both and dx=0 hold, with the comoving velocity v_co=τu^′/u. Thus we have established an unambiguous relation between proper and cosmic time, for all observers, galactic, uniformly moving, and accelerated.

We consider two uniformly moving or galactic observers (κ_A,ν_A) and (κ_B,ν_B) (cf. (5)) with geodesic rest frames (t,x) and (t^′,x^′), respectively (cf. (8)) connected by a boost (3) with relative speed,

In the frame (t,x), the worldline of observer (κ_A,ν_A) is x=−ν_A, and his proper time relates to cosmic time as , so that (cf. (6)). The worldline of observer (κ_B,ν_B) reads in this frame (cf. (7)) and if parametrized by cosmic time,

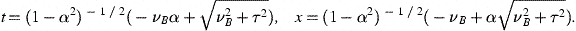
We so find the cosmic time differentials

with the comoving velocity υ_co(τ) defined in (6) (ν=ν_B). The time differential in (14) is not to be confused with the proper time of observer (κ_B,ν_B), as dx does not vanish. The equations following (12) also hold in the (t^′,x^′)-frame, with the replacements (t,x)→(t^′,x^′) and α→−α (that is κ_A↔κ_B in (12)), as well as ν_B↔ν_A, so that the proper time of (κ_B,ν_B) is given by . Thus the proper time differentials of the observers compare as

and this also applies to accelerated observers, with υ_co=τu^′(τ)/u.

Remark

This synchronization applies to general Roberson–Walker cosmologies as well, since the relations (15) between the time differentials remain valid for arbitrary expansion factors a(τ), if we use υ_co=a(τ)u^′(τ)/u (cf. [14]). However, the Milne universe has the distinct advantage of admitting globally geodesic rest frames, which make the global synchronization explained above possible. In any other Roberson–Walker cosmology, except for the static Minkowski universe, one would have to use chains of locally geodesic neighborhoods as a substitute. Locally geodesic chains are frequently invoked in mathematical proofs, but this method of synchronization is singularly impractical and never carried out explicitly. The question is, whether the globally geodesic synchronization of the Milne universe can be maintained for a general expansion factor. This is indeed the case, as the space expansion can be mimicked by contracting measuring rods [15]. In a genuine Robertson–Walker cosmology, the measuring rods are the galaxies themselves, the invariable galactic diameters, unaffected by the space expansion. Instead of scaling the intergalactic distances, we may equally well scale down the galactic diameters. (This time scaling is not to be confused with the fractal cluster scaling discussed in the reviews [16] and [17].) It suffices to consider a static or, for that matter, linearly expanding Robertson–Walker cosmology, and to scale the fundamental constants with an arbitrary scale factor a(τ), so that their dimensionless ratios stay constant. The latter condition is necessary to assure that atomic and nuclear radii or clock rates etc. scale in the same way. The interaction constants depend on cosmic time, and the Lagrangians are not any more covariant, but this is not required in an absolute space–time. Arbitrary deviations from linear expansion can be scaled into the fundamental constants, without spoiling the synchronization of the Milne universe. In practice, there is a local weight factor attached to every measuring rod, which determines the actual size of the space and time intervals [15]. In a general Robertson–Walker cosmology (with negatively curved 3-space), we may preserve the globally geodesic coordinate frames of the Milne universe by virtue of space–time dependent fundamental constants.

3. Conclusion: Time dilation without paradox

The time dilation and its experimental confirmation is commonly perceived as one of the pillars of relativity theory. In Section 2, we demonstrated that it can be derived without recourse to the relativity principle, by synchronizing the proper time of individual observers with the universal cosmic time. I conclude by comparing the cosmological with the relativistic interpretation of the time dilation, a further example illustrating the absolute space–time conception worked out in [18] and [19].

In a relativistic context, the clock or twin paradox refers to the difficulty to decide which observer (twin) ages faster, because none of them is preferred according to the relativity principle. Each of them can claim that his counterpart ages more slowly. To resolve this, an asymmetry has to be found which distinguishes one of the twins. The asymmetry is often pinpointed as an acceleration, which rescues the relativistic interpretation of the time dilation. This acceleration may have happened in the distant past, and it still determines whose claim has the priority, the accelerated twin loses. Cosmic time, however, provides a more straightforward, non-relativistic explanation.

The finite proper time interval,

may be identified with particle lifetimes, atomic transition periods, nuclear half-lives, or the observer’s biological age, but the crucial point here is that this interval is completely determined by his movement in the galaxy background. The expanding galaxy grid constitutes the reference frame defining cosmic time, the proper time of galactic observers can be identified with cosmic time, and the proper time intervals of all other observers, geodesic or accelerated, compare as in (15). The observers’ relative speed does not enter in (15), and therefore a clock paradox does not arise. They may undergo accelerations, but this is not necessary to consider when comparing their age, which they can do at any time, nor is a round trip necessary, frequently considered in discussions of the clock paradox. In special relativity theory, if both observers are uniformly moving, the time dilation can either mean or , depending on how the measurement is carried out, e.g., how many clocks are used and by whom; this generates the asymmetry needed to decide which of these formulas applies. By contrast, in a cosmological context, we need not enter the intricacies of clock transport and accelerated frames to resolve an emerging paradox. The proper time intervals (16) integrated over cosmic time are unambiguously determined by the individual comoving velocities in the receding galaxy background.

Acknowledgements

The author acknowledges the support of the Japan Society for the Promotion of Science. The hospitality and stimulating atmosphere of the Centre for Nonlinear Dynamics, Bharathidasan University, Trichy, and the Institute of Mathematical Sciences, Chennai, are likewise gratefully acknowledged. In particular, I would like to thank Nandor Balazs for reminding me of the clock paradox.