Causality violation in e+e− pair production by superluminal neutrinos
R. Tomaschitz 2012 EPL 98
19001
doi:10.1209/0295-5075/98/19001
Received 6 February 2012, accepted for publication 12 March 2012
Published 13 April 2012
Abstract
Pair emission by superluminal neutrinos is shown to be
causality violating in the 10–50 GeV range covered by the OPERA
experiment. Thus, the energy density of a freely propagating
superluminal neutrino current is not affected by energy loss due to e+
e−
pair creation, in accordance with the unperturbed energy profile
observed by ICARUS. Interaction processes involving sub- and
superluminal particles give rise to time inversions in the rest frames
of the subluminal constituents, resulting in causality violating
predetermination. Therefore, kinematic causality constraints in
addition to energy-momentum conservation are necessary to exclude
causality violation outside the lightcone. Electron-positron pair
production 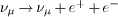 by superluminal muon neutrinos is forbidden in the OPERA energy range,
as the kinematic constraints on the neutrino frequencies and wave
vectors required by causality and energy-momentum conservation cannot
simultaneously be satisfied.
by superluminal muon neutrinos is forbidden in the OPERA energy range,
as the kinematic constraints on the neutrino frequencies and wave
vectors required by causality and energy-momentum conservation cannot
simultaneously be satisfied.
Introduction
OPERA reported a preliminary measurement of a superluminal
neutrino speed υ/c−1≈2.4 ± 0.6×10−5
at an average energy of 17 GeV, inferred from a muon neutrino beam over
a baseline of 730 km between the source at CERN and the OPERA detector
at Gran Sasso [1].
Doubts regarding this excess speed have been raised by the ICARUS
collaboration, who confirmed an undistorted energy profile of the
freely propagating neutrino current [2]
and found no evidence for a superluminal neutrino velocity [3].
Their objections were based on an untested energy loss rate, assuming
pair emission 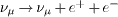 ,
and predicting a cutoff in the energy distribution at 13 GeV. This pair
creation requires a superluminal neutrino speed, otherwise the
kinematic constraints due to energy-momentum conservation cannot be
met. Since there was no cutoff observable in the energy distribution of
the CERN neutrino beam arriving at Gran Sasso, nor any direct evidence
of e+
e−
pair events in the ICARUS detector, it was argued that the neutrinos
cannot be superluminal [2].
,
and predicting a cutoff in the energy distribution at 13 GeV. This pair
creation requires a superluminal neutrino speed, otherwise the
kinematic constraints due to energy-momentum conservation cannot be
met. Since there was no cutoff observable in the energy distribution of
the CERN neutrino beam arriving at Gran Sasso, nor any direct evidence
of e+
e−
pair events in the ICARUS detector, it was argued that the neutrinos
cannot be superluminal [2].
Here, we show that pair production by superluminal neutrinos is forbidden in the OPERA energy range by causality violation. Energy-momentum conservation does not suffice to guarantee causal connections in an interaction process with sub- and superluminal constituents. Outside the lightcone, additional kinematic constraints have to be satisfied for an interaction to be causal.
We discuss superluminal signal transfer in an absolute spacetime conception, which allows to unambiguously distinguish causal from acausal connections by virtue of a universal cosmic time order. The absolute spacetime is manifested by a dispersive aether, the medium of wave propagation [4–6], and wave equations couple by a permeability tensor to the aether. The rest frame of the aether (aether frame) constitutes a distinguished frame of reference in which the permeability tensor is isotropic. The aether frame coincides with the rest frame of the cosmic microwave background radiation defined by vanishing temperature dipole anisotropy [7]. The Solar system barycenter is moving in the aether frame with a speed of υ/c≈ 1.23×10−3 [8–11].
Inertial rest frames of subluminal particles have a
well-defined relative speed 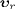 in the aether. The permeability tensor is anisotropic in moving
inertial frames, depending on this relative speed. Superluminal
particles propagating with speed
in the aether. The permeability tensor is anisotropic in moving
inertial frames, depending on this relative speed. Superluminal
particles propagating with speed 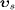 in the aether frame (υs>
1,
in the aether frame (υs>
1, 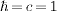 from now on) establish spacelike connections, whose time order can be
overturned by Lorentz boosts. As a consequence, the cosmic time order
of the aether frame appears inverted in the proper time of subluminal
particles, resulting in causality violation [12–14].
To maintain causality in an interaction process involving sub- and
superluminal particles, kinematic causality constraints are required in
addition to energy-momentum conservation to preserve the time order of
the aether frame in the rest frames of the subluminal constituents.
These causality constraints are a set of inequalities,
from now on) establish spacelike connections, whose time order can be
overturned by Lorentz boosts. As a consequence, the cosmic time order
of the aether frame appears inverted in the proper time of subluminal
particles, resulting in causality violation [12–14].
To maintain causality in an interaction process involving sub- and
superluminal particles, kinematic causality constraints are required in
addition to energy-momentum conservation to preserve the time order of
the aether frame in the rest frames of the subluminal constituents.
These causality constraints are a set of inequalities, 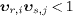 ,
where
,
where 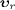 and
and 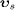 are the velocities (in the aether frame) of the interacting sub- and
superluminal particles labeled by i
and j,
respectively. If one of these inequalities is violated, a time
inversion will occur in the rest frame of the respective subluminal
particle. The pair production
are the velocities (in the aether frame) of the interacting sub- and
superluminal particles labeled by i
and j,
respectively. If one of these inequalities is violated, a time
inversion will occur in the rest frame of the respective subluminal
particle. The pair production 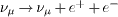 requires four inequalities
requires four inequalities 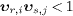 ,
where index i=e,p
labels the subluminal speed of electron and positron, and index j=1,2
the superluminal velocity of the in- and outgoing neutrino.
,
where index i=e,p
labels the subluminal speed of electron and positron, and index j=1,2
the superluminal velocity of the in- and outgoing neutrino.
Neutrinos freely propagating in the aether are described by the Dirac equation γμ gμν ψ,ν+mψ=0 coupled to a real symmetric permeability tensor gμν (ω), which depends on the frequency of the spinor modes ψ∝ eikμ xμ [6]. The sign convention for the Minkowski metric is ημν=diag(-1,1,1,1), so that the Dirac matrices satisfy γμ γν+γν γμ=2ημν, where γ0 is anti-Hermitian and the γi are Hermitian. Indices are raised and lowered with the Minkowski metric. In the aether frame, the permeability tensor is isotropic, g00=−ε (ω), gik=δik /μ (ω), g0k=0, where ε and μ are real positive permeabilities. To obtain the dispersion relation for the wave vector of the spinorial plane waves, we square the Dirac equation,

The squared permeability tensor hμν=gμα ηαβgβν is likewise isotropic,
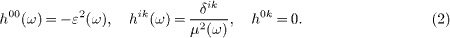
By substituting the plane waves ψ∝ eikμ xμ, kμ=(-ω, k), into the Klein-Gordon equation (1), we find the dispersion relation hαβ kα kβ+m2=0. This relation is equivalent to the Hamilton-Jacobi equation, if we identify kμ=S,μ, so that the classical action S=kμ xμ coincides with the phase of the elementary waves. Employing the diagonal permeability tensor hμν in (2), we find k(ω )=k(ω )k0, with a constant unit vector k0 and a positive wave number k(ω) defined by the dispersion relation k2=μ2 (ε2 ω2−m2) [6].
In this article, we study dispersive superluminal wave propagation in moving inertial frames, deriving anisotropic dispersion relations and neutrino Doppler shifts depending on the refractive index of the aether. The focus is on pair creation by superluminal neutrinos, illustrating causality violation outside the lightcone.
↑ ClosePair creation 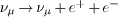 by superluminal neutrinos? Energy-momentum and causality constraints
by superluminal neutrinos? Energy-momentum and causality constraints
The electron and positron wave vectors are denoted by ki, i=e,p, the wave numbers by ki, and the frequencies by ωi. The neutrino variables are kνj, kνj, and ωνj, where the index j=1,2 refers to the in- and out-states. The dispersion relations defining the frequency dependence of the wave numbers in the aether frame read, cf. (2),
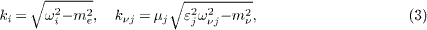
where me is the electron mass and mν a possible neutrino mass of a few eV. The index i=e,p labels electron and positron; kν 1 and kν 2 are the wave numbers of the neutrino in- and out-states, respectively. The permeabilities εj=ε (ωνj) and μj=μ (ωνj), j=1,2, depend on the neutrino frequencies.
Energy and momentum conservation implies the constraints
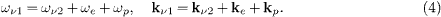
We consider aligned in- and outgoing neutrino momenta, kνj=kνj kν ,0, where kν ,0 is the neutrino unit wave vector. We also assume that electron and positron have the same emission angle ki,0 kν ,0=cosθ, 0 ≤θ ≤π /2, and thus the same energy ωi=δω ν /2, δω ν=ων 1−ων 2. On multiplying the momentum conservation (4) by kν ,0, we obtain

where δkν=kν 1−kν 2. The same identity is found by squaring the momentum relation.
The four kinematic causality constraints mentioned in the introduction read
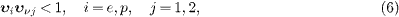
where 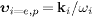 denotes the speed of electron and positron, and
denotes the speed of electron and positron, and 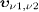 are the superluminal velocities of the incoming (ν 1)
and outgoing (ν 2) neutrino,
defined by the group velocity of the wave modes, cf. (7).
All velocities refer to the aether frame. The constraints (6)
are necessary and sufficient to prevent causality-violating time
inversions in the proper time of electron and positron, and will be
derived in (26)−(33).
In this section, we show that inequalities (6)
cannot be satisfied in the energy range of the OPERA experiment.
are the superluminal velocities of the incoming (ν 1)
and outgoing (ν 2) neutrino,
defined by the group velocity of the wave modes, cf. (7).
All velocities refer to the aether frame. The constraints (6)
are necessary and sufficient to prevent causality-violating time
inversions in the proper time of electron and positron, and will be
derived in (26)−(33).
In this section, we show that inequalities (6)
cannot be satisfied in the energy range of the OPERA experiment.
We write the neutrino velocity as 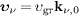 ,
where kν
,0 is the unit wave vector of the
neutrino. The group velocity υgr
is defined by the frequency derivative of the wave number (3) [6,15,16],
,
where kν
,0 is the unit wave vector of the
neutrino. The group velocity υgr
is defined by the frequency derivative of the wave number (3) [6,15,16],
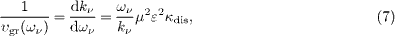
where κdis is the dispersion measure
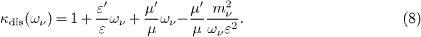
The primes denote frequency derivatives of the permeabilities ε (ων) and μ (ων). (We here drop the index j labeling in- and out-states.) If the permeabilities are constant, we find κdis=1. We assume a positive group velocity, which means a positive dispersion measure κdis> 0, as the permeabilities are nearly constant in the OPERA energy range [6]. Negative group velocities are possible [17,18], but require substantial logarithmic derivatives of the permeabilities to change the sign of κdis. The neutrino velocity thus reads
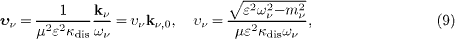
where υν=υgr denotes the absolute value; we will also use υνj to label the in- and outgoing neutrino. Clearly, υν≤ 1/(με κdis), where equality is attained at zero neutrino mass. Thus, a superluminal neutrino speed can only be attained if με κdis < 1, which is better seen by writing the neutrino energy and wave number as
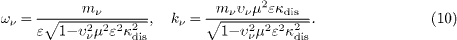
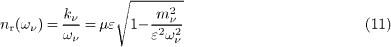
and its frequency derivative completely determine the neutrino velocity (9) at any given frequency,
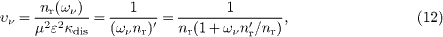
as well as the wave number kν=ων nr (ων). In the massless case, mν=0, we have nr=με.
The causality conditions 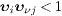 in (6)
can be expressed in terms of the refractive index. The neutrino
velocity is
in (6)
can be expressed in terms of the refractive index. The neutrino
velocity is 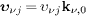 ,
with υνj
in (12).
The electron and positron velocities are
,
with υνj
in (12).
The electron and positron velocities are 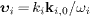 ,
with the wave numbers ki
in (3).
On substituting these velocities into the causality
constraints (6),
we obtain
,
with the wave numbers ki
in (3).
On substituting these velocities into the causality
constraints (6),
we obtain

where nr,j=nr (ωνj). The in- and outgoing neutrino variables are labeled by j=1,2, and the electron and positron variables by i=e,p. Since the electron and positron velocities give identical inequalities, we end up with two constraints (j=1,2), cf. after (4),
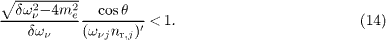
By substituting the emission angle (5), we obtain δkν /δω ν< (ωνj nr,j)', or more explicitly,
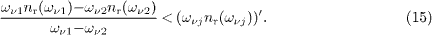
The left-hand side can be replaced by the derivative 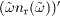 ,
where
,
where 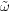 is a frequency in the interval
is a frequency in the interval 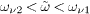 (mean value theorem), so that the causality conditions read
(mean value theorem), so that the causality conditions read 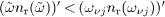 ,
j=1,2.
In terms of the neutrino group velocity (12),
this means
,
j=1,2.
In terms of the neutrino group velocity (12),
this means 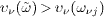 .
As υν
(ω) is monotonically increasing in the OPERA
energy range, the first of these inequalities, j=1,
is violated. At 13.8 GeV, 28.2 GeV, and 40.7 GeV, the preliminary
result for the excess speed υν−1
is 2.25×10−5,
2.5×10−5
and 2.8×10−5,
respectively [1].
In an energy range where the excess speed is decreasing, the second
condition
.
As υν
(ω) is monotonically increasing in the OPERA
energy range, the first of these inequalities, j=1,
is violated. At 13.8 GeV, 28.2 GeV, and 40.7 GeV, the preliminary
result for the excess speed υν−1
is 2.25×10−5,
2.5×10−5
and 2.8×10−5,
respectively [1].
In an energy range where the excess speed is decreasing, the second
condition 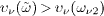 is violated. Only if the group velocity υν (ω)
has a peak between the in- and outgoing neutrino frequencies, both
causality constraints can be met.
is violated. Only if the group velocity υν (ω)
has a peak between the in- and outgoing neutrino frequencies, both
causality constraints can be met.
Anisotropic permeability tensor and Doppler-shifted neutrino frequencies in moving inertial frames
We consider an inertial frame moving in the aether with
constant relative velocity 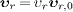 .
Zero subscripts denote unit vectors. The spacetime coordinates of the
aether frame are denoted by xμ=(t,x),
and of the inertial frame by x'μ=(t',x').
The proper orthochronous Lorentz boost x'μ=Λν
(-1)μxν
relating the frames reads
.
Zero subscripts denote unit vectors. The spacetime coordinates of the
aether frame are denoted by xμ=(t,x),
and of the inertial frame by x'μ=(t',x').
The proper orthochronous Lorentz boost x'μ=Λν
(-1)μxν
relating the frames reads
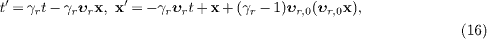
with Lorentz factor γr=(1-υr2)−1/2,
so that 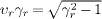 .
We can thus identify
.
We can thus identify
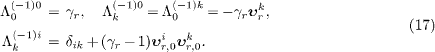
The inverse transformation, xμ=Λν
μx'ν,
is obtained by changing the sign of the (always subluminal) relative
velocity 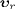 .
The speed
.
The speed 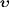 of a uniformly moving sub- or superluminal particle in the aether frame
transforms as, cf. [6]
and (33),
of a uniformly moving sub- or superluminal particle in the aether frame
transforms as, cf. [6]
and (33),
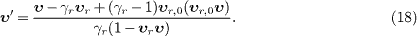
Primed quantities refer to the inertial frame. This transformation preserves sub- and superluminal velocities, cf. (25).
The wave 4-vectors defining the phase of plane waves are denoted by kμ=(-ω, k) in the aether frame, and by k'μ=(-ω',k') in the inertial frame. They transform covariantly, k'μ=kα Λμ α, as
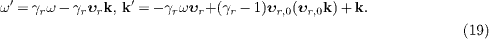
The permeability tensor hμν, cf. (1) and (2), transforms contravariantly, h'μν=hαβ Λα (-1)μΛβ(-1)ν, and is anisotropic in the inertial frame,
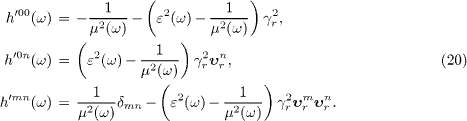
Relativistic covariance is abandoned, as this tensor depends on the frequency of the wave modes in the aether frame. The dispersion relation h'μνk'μk'ν+m2=0 is satisfied by k'μ=(-ω',k') in (19), and the classical action coinciding with the phase stays invariant, S=S'=k'μx'μ, cf. after (2). As the wave 4-vectors transform linearly, the energy-momentum constraints (4) also hold in primed variables ω' and k'.
For instance, we may consider the pair production discussed in
the previous section in the (e+
,e− ,ν 2)
center-of-mass frame, ν 2 being the
outgoing neutrino. This frame is obtained via the Lorentz
boost (16)
with relative speed 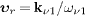 ,
so that υr=nr,1
< 1, where nr,1=nr
(ων 1) is the
refractive index at the frequency of the incoming neutrino ν 1,
cf. (11).
The neutrino momentum k'ν
1 vanishes, k'ν
1=k'ν 2+k'e+k'p=0,
cf. (19),
and we find the Doppler-shifted neutrino energy and speed in the
center-of-mass frame as
,
so that υr=nr,1
< 1, where nr,1=nr
(ων 1) is the
refractive index at the frequency of the incoming neutrino ν 1,
cf. (11).
The neutrino momentum k'ν
1 vanishes, k'ν
1=k'ν 2+k'e+k'p=0,
cf. (19),
and we find the Doppler-shifted neutrino energy and speed in the
center-of-mass frame as
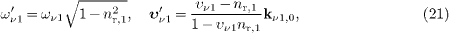
where υν 1=υν (ων 1) is the neutrino group velocity in the aether frame, cf. (9) and (12). In the center-of-mass frame, the incoming neutrino emerges without wave vector, k'ν 1=0, yet propagating at a well-defined superluminal speed and energy.
In the next section, we will study the kinematics of pair
emission, 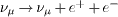 ,
in the rest frame of the electron, illustrating causality violation by
time inversion. (The discussion of the positron rest frame is
completely analogous, and the superluminal neutrino does not admit a
rest frame, as Lorentz boosts are subluminal.) We identify the relative
speed in eqs. (16)−(20)
with the electron velocity in the aether frame,
,
in the rest frame of the electron, illustrating causality violation by
time inversion. (The discussion of the positron rest frame is
completely analogous, and the superluminal neutrino does not admit a
rest frame, as Lorentz boosts are subluminal.) We identify the relative
speed in eqs. (16)−(20)
with the electron velocity in the aether frame, 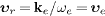 ,
so that the Lorentz factor reads γr=γe=(1-υe2)−1/2.
As for the neutrino wave numbers, we put kνj=ωνj
nr,j,
j=1,2,
cf. after (12)
and (13),
and substitute this into (19),
to find the Doppler-shifted in- and outgoing neutrino frequencies in
the electron rest frame,
,
so that the Lorentz factor reads γr=γe=(1-υe2)−1/2.
As for the neutrino wave numbers, we put kνj=ωνj
nr,j,
j=1,2,
cf. after (12)
and (13),
and substitute this into (19),
to find the Doppler-shifted in- and outgoing neutrino frequencies in
the electron rest frame,

Here, 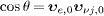 is the emission angle (5)
of the electron in the aether frame, and nr,j=nr
(ωνj)
the refractive index. We also note ω'e=me
and ω'p=ω'ν
1−ω'ν 2−me,
cf. (4).
Since nr
< 1 and υe
< 1, the neutrino frequencies ω'νj
stay positive in the electron's rest frame, cf. (22).
The positron frequency ω'p
in the electron rest frame is positive as well, since the Lorentz
boosts (16)
preserve the sign of energy of subluminal particles with timelike
4-momenta.
is the emission angle (5)
of the electron in the aether frame, and nr,j=nr
(ωνj)
the refractive index. We also note ω'e=me
and ω'p=ω'ν
1−ω'ν 2−me,
cf. (4).
Since nr
< 1 and υe
< 1, the neutrino frequencies ω'νj
stay positive in the electron's rest frame, cf. (22).
The positron frequency ω'p
in the electron rest frame is positive as well, since the Lorentz
boosts (16)
preserve the sign of energy of subluminal particles with timelike
4-momenta.
The electronic wave vector vanishes in the electron rest frame. As k'e=0, positron and neutrino wave vectors are related by k'p=k'ν 1−k'ν 2. The in- and outgoing neutrino wave vectors (labeled by j=1,2) in the electron's rest frame read, cf. (19),
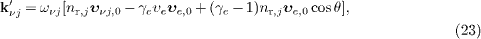
where we have identified the unit vectors of neutrino speed
and momentum in the aether frame, 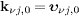 ,
cf. (9).
θ
is the electron emission angle as in (22).
The ratio k'νj
/ω'νj,
cf. (22)
and (23),
can be recovered from the neutrino velocity in the electron rest frame,
cf. (18),
,
cf. (9).
θ
is the electron emission angle as in (22).
The ratio k'νj
/ω'νj,
cf. (22)
and (23),
can be recovered from the neutrino velocity in the electron rest frame,
cf. (18),
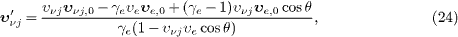
by replacing the neutrino group velocity υνj
in (24)
by the refractive index nr,j.
Group velocity and refractive index are related as stated in (12).
We also note the electron variables γe=ωe
/me
and 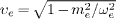 in (24).
By squaring eqs. (23)
and (24),
we find the absolute value υ'νj
of the neutrino velocities and the neutrino wave numbers k'νj,
in (24).
By squaring eqs. (23)
and (24),
we find the absolute value υ'νj
of the neutrino velocities and the neutrino wave numbers k'νj,
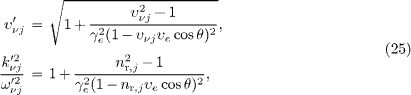
with ω'νj in (22) and nr,j=nr (ωνj). In the following, we discuss the real-space world lines of the in- and outgoing neutrino as they appear in the electron's proper time.
↑ CloseCausality violation by time inversion
In the preceding sections, we have studied the energy-momentum
variables of pair emission, 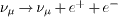 .
Here, we analyze the real-time kinematics. The coordinates of the
aether frame are denoted by (t,x).
The world lines of the in- and outgoing superluminal neutrino read
.
Here, we analyze the real-time kinematics. The coordinates of the
aether frame are denoted by (t,x).
The world lines of the in- and outgoing superluminal neutrino read 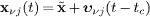 ,
j=1,2.
The world lines of electron and positron are
,
j=1,2.
The world lines of electron and positron are 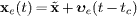 and
and 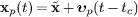 ,
respectively. At t=tc,
these four world lines coalesce at
,
respectively. At t=tc,
these four world lines coalesce at 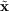 .
Neutrino ν 1 is emitted
by a source located at (t0
,xν 1 (t0
)), t0
<tc.
The electron-positron pair emission takes place at
.
Neutrino ν 1 is emitted
by a source located at (t0
,xν 1 (t0
)), t0
<tc.
The electron-positron pair emission takes place at 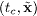 .
At a later instant t1>tc,
the positron is absorbed by a detector located at (t1
,xp
(t1 )),
the electron at (t1
,xe
(t1 )),
and neutrino ν 2 at (t1
,xν 2 (t1
)).
.
At a later instant t1>tc,
the positron is absorbed by a detector located at (t1
,xp
(t1 )),
the electron at (t1
,xe
(t1 )),
and neutrino ν 2 at (t1
,xν 2 (t1
)).
The electron rest frame is denoted by primed coordinates (t',x'),
and connected to the aether frame (t,x)
by the Lorentz boost (16),
with relative velocity 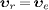 and γr=γe=(1-υe2)−1/2.
We discuss only the rest frame of the electron; the positron rest frame
can be dealt with in like manner. As mentioned, there is no rest frame
for superluminal particles [19],
as the relative speed defining Lorentz boosts is subluminal; a possible
neutrino mass in wave equation (1)
is not a rest mass if the neutrino is superluminal. The existence of a
rest frame in a permeable spacetime exclusively depends on the particle
speed, which has to be subluminal. If the particle is subluminal in the
aether frame, it remains so in any other inertial frame, and
analogously for superluminal velocities, cf. (18)
and (25).
and γr=γe=(1-υe2)−1/2.
We discuss only the rest frame of the electron; the positron rest frame
can be dealt with in like manner. As mentioned, there is no rest frame
for superluminal particles [19],
as the relative speed defining Lorentz boosts is subluminal; a possible
neutrino mass in wave equation (1)
is not a rest mass if the neutrino is superluminal. The existence of a
rest frame in a permeable spacetime exclusively depends on the particle
speed, which has to be subluminal. If the particle is subluminal in the
aether frame, it remains so in any other inertial frame, and
analogously for superluminal velocities, cf. (18)
and (25).
In the electron's rest frame (t',x'), we parametrize the world lines with the reference time of the aether frame. The world line (t'ν1(t),x'ν 1 (t)) of the incoming neutrino ν 1 reads
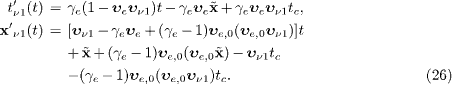
This is obtained by applying the Lorentz boost (16)
(with 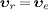 )
to the neutrino world line (t,xν
1 (t)) in
the aether frame as defined at the beginning of this section. The time
interval between the emission of neutrino ν 1 at t0
and the subsequent e+
e−
pair emission at tc
is
)
to the neutrino world line (t,xν
1 (t)) in
the aether frame as defined at the beginning of this section. The time
interval between the emission of neutrino ν 1 at t0
and the subsequent e+
e−
pair emission at tc
is
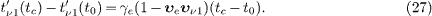
Thus, if the causality condition 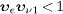 is violated, cf. (6),
the time order of neutrino emission and pair production is inverted in
the proper time of the emitted electron. This happens in the OPERA
energy range, where
is violated, cf. (6),
the time order of neutrino emission and pair production is inverted in
the proper time of the emitted electron. This happens in the OPERA
energy range, where 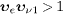 ,
cf. after (15).
As a consequence, neutrino ν 1 reemerges in
the electron rest frame during the electron's proper lifetime, which is
the interval between the pair creation at t'e
(tc)
and the absorption of the electron by the electron detector at a later
instant t'e
(t1).
This is causality violating, as the incoming neutrino ν 1
was annihilated at the time of pair creation by decay into the e+
e−
pair and neutrino ν 2 of lower
energy. In the universal reference time of the aether frame, neutrino ν 1
exists in the interval [t0
,tc ],
and the e+
e−
pair coexists with the outgoing neutrino ν 2 in the
disjoint interval [tc
,t1 ],
which is the electron's actual lifetime, cf. (29).
,
cf. after (15).
As a consequence, neutrino ν 1 reemerges in
the electron rest frame during the electron's proper lifetime, which is
the interval between the pair creation at t'e
(tc)
and the absorption of the electron by the electron detector at a later
instant t'e
(t1).
This is causality violating, as the incoming neutrino ν 1
was annihilated at the time of pair creation by decay into the e+
e−
pair and neutrino ν 2 of lower
energy. In the universal reference time of the aether frame, neutrino ν 1
exists in the interval [t0
,tc ],
and the e+
e−
pair coexists with the outgoing neutrino ν 2 in the
disjoint interval [tc
,t1 ],
which is the electron's actual lifetime, cf. (29).
The world line of the outgoing neutrino ν 2
and its lifetime in the electron rest frame are obtained by replacing
the subscript index ν 1 in
eqs. (26)
and (27)
by ν
2. In this case, the time order of the aether
frame is preserved, since the causality condition 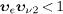 preventing a time inversion in the electron rest frame is met, cf.
after (15).
Neutrino ν 2 exists in
the interval [t'ν 2
(tc ),t'ν
2 (t1 )],
t'ν
2 (tc
) <t'ν 2 (t1),
covering part of or extending beyond the electron's proper lifetime [t'e
(tc )=t'ν
2 (tc
),t'e (t1
)]. It covers the electron's full lifespan if
preventing a time inversion in the electron rest frame is met, cf.
after (15).
Neutrino ν 2 exists in
the interval [t'ν 2
(tc ),t'ν
2 (t1 )],
t'ν
2 (tc
) <t'ν 2 (t1),
covering part of or extending beyond the electron's proper lifetime [t'e
(tc )=t'ν
2 (tc
),t'e (t1
)]. It covers the electron's full lifespan if
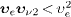 ,
since t'ν
2 (t1 )-t'e
(t1)
factorizes as
,
since t'ν
2 (t1 )-t'e
(t1)
factorizes as 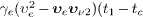 ),
cf. (28).
),
cf. (28).
Accordingly, the incoming neutrino ν 1 as well as the outgoing neutrino ν 2 simultaneously emerge in the rest frame of the electron, during the electron's proper lifetime, in violation of causality. Energy and momentum are not conserved either, even though the constraints (4) (in primed variables) are satisfied, since the in- and outgoing neutrinos exist at the same time in the electron's rest frame, propagating along different trajectories.
We consider the world line (t'e (t),x'e) of the electron in its rest frame (t',x'),
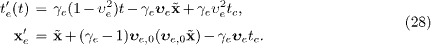
The electron's proper lifetime between its creation and absorption in the electron's rest frame is thus

contracted due to the relative motion in the aether [14]. We place the electron detector in a way that the electron is absorbed at a time t1 defined by equating t'e (t1 )=t'ν 1 (t0), cf. (26) and (28), which means
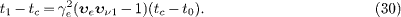
This choice of t1
is only possible if the causality condition 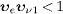 is violated, as the time intervals tc−t0
and t1−tc
are defined positive from the outset, cf. the beginning of this
section. The electron located at x'e
will be absorbed by the approaching detector at t'e
(t1).
Thus, in the electron rest frame, the incoming neutrino ν 1
coexists with the electron throughout the electron's proper lifetime in
the interval [t'e
(tc ),t'e
(t1 )],
since t'ν
1 (t0 )=t'e
(t1)
and
is violated, as the time intervals tc−t0
and t1−tc
are defined positive from the outset, cf. the beginning of this
section. The electron located at x'e
will be absorbed by the approaching detector at t'e
(t1).
Thus, in the electron rest frame, the incoming neutrino ν 1
coexists with the electron throughout the electron's proper lifetime in
the interval [t'e
(tc ),t'e
(t1 )],
since t'ν
1 (t0 )=t'e
(t1)
and
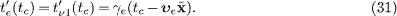
In this time interval [t'e (tc ),t'e (t1 )], neutrino ν 1 moves from x'ν 1 (tc )=x'e to
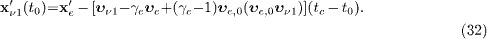
Combining this with the time inversion (27), we may write
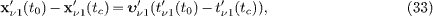
where 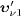 is the neutrino speed in the electron rest frame as stated in (24).
In this way, we have also recovered the addition law (18).
is the neutrino speed in the electron rest frame as stated in (24).
In this way, we have also recovered the addition law (18).
To summarize, the Lorentz boost relating the aether frame to
the electron's rest frame maps the world line of the incoming neutrino ν 1
into the proper lifetime of the electron. The reason for this is the
time inversion (27),
which occurs since the causality constraint 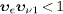 is violated. Analogous reasoning holds for the positron rest frame. The
causality conditions preventing a time inversion in the electron and
positron rest frames are
is violated. Analogous reasoning holds for the positron rest frame. The
causality conditions preventing a time inversion in the electron and
positron rest frames are 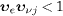 and
and 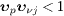 ,
where
,
where 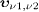 are the velocities of the in- and outgoing neutrino; the electron,
positron and neutrino velocities all refer to the aether frame.
are the velocities of the in- and outgoing neutrino; the electron,
positron and neutrino velocities all refer to the aether frame.
More generally, in an interaction process involving sub- and
superluminal particles, the causality conditions 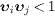 have to be met, where index i
labels the velocities of the subluminal particles in the aether frame,
and index j
the superluminal velocities. These conditions are necessary and
sufficient to avoid time inversion and thus causality violation in the
rest frames of the subluminal particles taking part in the interaction.
Pion and kaon decay
have to be met, where index i
labels the velocities of the subluminal particles in the aether frame,
and index j
the superluminal velocities. These conditions are necessary and
sufficient to avoid time inversion and thus causality violation in the
rest frames of the subluminal particles taking part in the interaction.
Pion and kaon decay 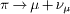 into subluminal muons and superluminal neutrinos [20,21],
and the causality constraints on photon emission by superluminal
charges,
into subluminal muons and superluminal neutrinos [20,21],
and the causality constraints on photon emission by superluminal
charges, 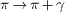 ,
will be discussed elsewhere.
,
will be discussed elsewhere.
Conclusion
Causality implies that 1) every effect has a cause; that 2) the cause precedes the effect; and 3) the distinction of cause and effect is unambiguous. Superluminal energy transfer establishes spacelike connections, whose time order can be altered by Lorentz boosts, so that different inertial observers see a different time order. Thus superluminal signal transfer violates either condition 2) or 3) in a relativistic context, as observations made in different inertial frames have to be regarded as equally real. There have been suggestions that acausal relativistic signal transfer is not logically inconsistent [22]. However, the predetermination that goes with effects preceding their causes lends itself better to science fiction than to an empirical science.
Causality violation in superluminal signal transfer is conceptually different from the acausal advanced wave fields of electrodynamics. So long as the signal transfer happens at the speed of light or is subluminal, acausal solutions of evolution equations can unambiguously be identified. Maxwell's equations admit acausal solutions generated by advanced Green functions. If the signal is (sub)luminal, Lorentz boosts cannot alter the time order of events connected by the signal. Thus a retarded or advanced solution remains so in all inertial frames, and one can discard advanced solutions on the grounds of causality violation.
Signal transfer by superluminal neutrinos requires a universal frame of reference to discern causal from acausal connections, as Lorentz boosts can change the time order of emission and absorption. There are two groups (equivalence classes) of inertial observers; one sees the emission prior to absorption in their proper time, and the second observes a time-inverted neutrino current propagating from the detector toward the source. The reference frame allows both groups to unambiguously discern cause and effect. All observers can compare their proper time to the universal time order defined by the reference frame, and thus determine whether a time inversion (27) occurs in their rest frames due to their motion in the aether [5,7,14]. In contrast, superluminal signal transfer in conjunction with a relativistic interpretation of the Lorentz symmetry conflicts with causality, as cause and effect cannot invariantly be identified: what appears causal to one observer, is acausal for another. Thus, unlike in electrodynamics, a reference frame is necessary to discriminate causal and acausal solutions of evolution equations. Here, we have identified the emission of an e+ e− pair as an acausal solution of the energy-momentum conditions.
The speed of signal transfer (7)
is determined by a dispersion relation, which depends on the particle
mass and the permeability tensor by which the wave equation is coupled
to the aether. Different particles couple with different permeability
tensors. The universal frame of reference is identified as the aether
frame in which the permeability tensors are isotropic, cf. (2)
and (20),
and is manifested as the rest frame of the cosmic microwave background.
Inertial frames are connected to the aether frame by Lorentz boosts and
characterized by a subluminal relative velocity 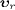 in the aether. When calculating cross-sections of interactions outside
the lightcone, involving sub- and superluminal particles, one has to
take account of kinematic causality conditions. The constraints
necessary and sufficient to exclude causality-violating time inversions
in the rest frames of the subluminal constituents are a set of
inequalities
in the aether. When calculating cross-sections of interactions outside
the lightcone, involving sub- and superluminal particles, one has to
take account of kinematic causality conditions. The constraints
necessary and sufficient to exclude causality-violating time inversions
in the rest frames of the subluminal constituents are a set of
inequalities 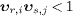 .
The
.
The 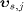 denote the group velocities of the superluminal modes, and the
denote the group velocities of the superluminal modes, and the 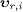 are the velocities of the subluminal particles in the interaction
process with rest frames defined by the Lorentz boosts (16);
all velocities refer to asymptotic in- and out-states in the aether
frame. These causality constraints prohibit pair emission by
superluminal neutrinos in the OPERA energy range.
are the velocities of the subluminal particles in the interaction
process with rest frames defined by the Lorentz boosts (16);
all velocities refer to asymptotic in- and out-states in the aether
frame. These causality constraints prohibit pair emission by
superluminal neutrinos in the OPERA energy range.
References
- [1]
- Adam T. et al arXiv:1109.4897 (2011) Preprint
- [2]
- Antonello M. et al arXiv:1110.3763 (2011) Preprint
- [3]
- Antonello M. et al arXiv:1203.3433 (2012) Preprint
- [4]
- Tomaschitz R. 2001 Class. Quantum Grav. 18 4395 IOPscience
- [5]
- Tomaschitz R. 2007 Ann. Phys. (N.Y.)
322 677 CrossRef
- [6]
- Tomaschitz R. 2012 EPL 97 39003 IOPscience
- [7]
- Tomaschitz R. 2000 Celest. Mech. Dyn.
Astron. 77 107 CrossRef
- [8]
- Kogut A. et al 1993 Astrophys.
J. 419 1 CrossRef
- [9]
- Fixsen D. J. et al 1996 Astrophys. J. 473 576 IOPscience
- [10]
- Hinshaw G. et al 2009 Astrophys. J., Suppl. Ser. 180 225 IOPscience
- [11]
- Jarosik N. et al 2011 Astrophys. J., Suppl. Ser. 192 14 IOPscience
- [12]
- Tomaschitz R. 1996 Chaos, Solitons
Fractals 7 753 CrossRef
- [13]
- Tomaschitz R. 2000 Int. J. Mod. Phys.
A 15 3019
- [14]
- Tomaschitz R. 2004 Chaos, Solitons
Fractals 20 713 CrossRef
- [15]
- Landau L. D. and Lifshitz E. M. 1984 Electrodynamics
of Continuous Media (Oxford: Pergamon)
- [16]
- Brillouin L. 1988 Wave Propagation
and Group Velocity (New York: Academic Press)
- [17]
- Gehring G. M. et al 2006 Science
312 895 CrossRef
- [18]
- Tomaschitz R. 2010 Eur. Phys. J. C
69 241 CrossRef
- [19]
- Cohen A. G. and Glashow S. L. 2011 Phys.
Rev. Lett. 107 181803 CrossRef
- [20]
- Bi X.-J. et al 2011 Phys.
Rev. Lett. 107 241802 CrossRef
- [21]
- Cowsik R. et al 2011 Phys.
Rev. Lett. 107 251801 CrossRef
- [22]
- Newton R. 1970 Science 167
1569 CrossRef
- [1]
- Adam T. et al arXiv:1109.4897 (2011) Preprint
- [2]
- Antonello M. et al arXiv:1110.3763 (2011) Preprint
- [3]
- Antonello M. et al arXiv:1203.3433 (2012) Preprint
- [4]
- Tomaschitz R. 2001 Class. Quantum Grav. 18 4395 IOPscience
- [5]
- Tomaschitz R. 2007 Ann. Phys. (N.Y.)
322 677 CrossRef
- [6]
- Tomaschitz R. 2012 EPL 97 39003 IOPscience
- [7]
- Tomaschitz R. 2000 Celest. Mech. Dyn.
Astron. 77 107 CrossRef
- [8]
- Kogut A. et al 1993 Astrophys.
J. 419 1 CrossRef
- [9]
- Fixsen D. J. et al 1996 Astrophys. J. 473 576 IOPscience
- [10]
- Hinshaw G. et al 2009 Astrophys. J., Suppl. Ser. 180 225 IOPscience
- [11]
- Jarosik N. et al 2011 Astrophys. J., Suppl. Ser. 192 14 IOPscience
- [12]
- Tomaschitz R. 1996 Chaos, Solitons
Fractals 7 753 CrossRef
- [13]
- Tomaschitz R. 2000 Int. J. Mod. Phys.
A 15 3019
- [14]
- Tomaschitz R. 2004 Chaos, Solitons
Fractals 20 713 CrossRef
- [15]
- Landau L. D. and Lifshitz E. M. 1984 Electrodynamics
of Continuous Media (Oxford: Pergamon)
- [16]
- Brillouin L. 1988 Wave Propagation
and Group Velocity (New York: Academic Press)
- [17]
- Gehring G. M. et al 2006 Science
312 895 CrossRef
- [18]
- Tomaschitz R. 2010 Eur. Phys. J. C
69 241 CrossRef
- [19]
- Cohen A. G. and Glashow S. L. 2011 Phys.
Rev. Lett. 107 181803 CrossRef
- [20]
- Bi X.-J. et al 2011 Phys.
Rev. Lett. 107 241802 CrossRef
- [21]
- Cowsik R. et al 2011 Phys.
Rev. Lett. 107 251801 CrossRef
- [22]
- Newton R. 1970 Science 167
1569 CrossRef