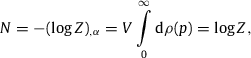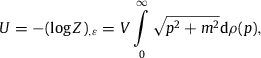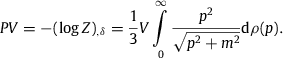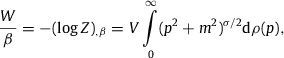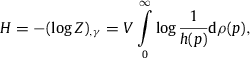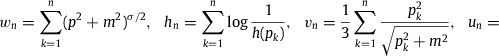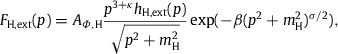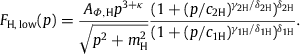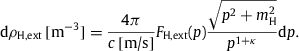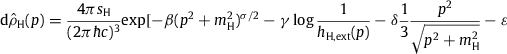Highlights
- •
A spectral fit to the ultra-high energy flux of cosmic-ray nuclei exhibits subexponential Weibull decay.
- •
The spectral number density of the nuclear gas is a multiply broken power-law distribution with Weibull cutoff.
- •
The thermodynamics of a stationary non-equilibrium gas of relativistic nuclei is developed, starting with the entropy functional in phase space.
- •
The heat capacities, compressibilities and the expansion coefficient of a relativistic gas mixture in stationary non-equilibrium are derived.
- •
Estimates of temperature, number count, internal energy and pressure of the all-particle cosmic-ray flux.
Abstract
The spectral number density of cosmic-ray nuclei is shown to be a multiply broken power law with subexponential spectral cutoff. To this end, a spectral fit is performed to data sets covering the 1GeV−1011GeV interval of the all-particle cosmic-ray spectrum. The flux points of the ultra-high energy spectral tail measured with the Telescope Array indicate a Weibull cutoff exp(−(E∕(kBT))σ) and permit a precise determination of the cutoff temperature kBT=(2.5±0.1)×1010 GeV and the spectral index σ=0.66±0.02. Based on the spectral number density inferred from the least-squares fit, the thermodynamics of this stationary non-equilibrium system, a multi-component mixture of relativistic nuclei, is developed. The derivative of entropy with respect to internal energy defines the effective temperature of the nuclei, S,U=1∕Teff,kBTeff≈16.1 GeV, and the functional dependence between the cutoff temperature in the Weibull exponential and the effective gas temperature is determined. The equipartition ratio is found to be U∕(NkBTeff)≈0.30. The isochoric and isobaric heat capacities of the nuclear gas are calculated, as well as the isothermal and adiabatic compressibilities and the isobaric expansion coefficient, and it is shown that this non-equilibrated relativistic gas mixture satisfies the thermodynamic inequalities 0<CV<CP and 0<κS<κTeff.
Keywords
- Subexponential spectral decay;
- Entropy of stationary non-equilibrium ensembles;
- Weibull entropy and excess entropy;
- Multiply broken power-law densities with Weibull cutoff;
- Heat capacities of a non-equilibrated gas mixture;
- Thermodynamics of cosmic-ray nuclei
1. Introduction
We discuss the thermodynamics of the all-particle cosmic-ray spectrum which has recently been measured over an extended energy range by several ground-based, balloon- and space-borne experiments [1]; [2]; [3]; [4]; [5]; [6]; [7]; [8] ; [9]. The spectrum comprises relativistic nuclei with energies ranging from 1GeV to 1011GeV, and the measurements are sufficiently precise to reveal the spectral fine structure. In double-logarithmic representation, the wideband spectral map consists of multiple power-law slopes with smooth transitions at the spectral breaks, terminating with a subexponential spectral cutoff above 1010GeV.
The purpose of this paper is to model the spectral fine structure. Ab initio modeling of the cosmic ray flux based on kinetic equations requires to quantify the driving forces sustaining the stationary non-equilibrium, that is the production sites and acceleration and attenuation mechanisms as well as the nuclear mass composition, which are only vaguely known [10] ; [11]. Numerical simulations suggest that protons can be accelerated up to a few 106GeV by diffusive shock acceleration in supernova remnants, and iron nuclei up to 108GeV. Direct evidence for that is still lacking, as there are no intensity peaks in anisotropy maps which can be associated with specific remnants. Another Galactic driving mechanism is acceleration in the electric fields of pulsars. Ultra-high energy cosmic rays above 108GeV are believed to be of extragalactic origin. If these rays are predominantly protons, the spectral cutoff could stem from energy dissipation due to scattering by background photons. Another possible attenuation effect at ultra-high energies is photo-disintegration of heavier nuclei. The cutoff could also be caused by acceleration limits at the production sites. As ab initio modeling of the wideband fine structure is presently not a viable option owing to the uncertain production and interaction mechanisms, we will content ourselves with a reconstruction of the spectral density from the available data sets. We will treat cosmic-ray nuclei as a relativistic gas in stationary non-equilibrium, as the cosmic-ray flux does not change on accessible time scales, apart from solar modulations at low energy which are already averaged out in the data sets. We will also dissect the entropy functional of the empirical spectral density to characterize the deviation from equilibrium, which can be done quantitatively without specification of the driving forces as outlined below.
The spectral flux density extending over eleven decades in energy can be fitted by a multiply broken power-law distribution with a subexponential spectral cutoff at ultra-high energies. The measured subexponential spectral decay means to replace the Boltzmann factor in the flux density by the Weibull factor exp(−(E∕(kBT))σ) with spectral index (shape parameter) 0<σ<1 [12] ; [13], also known as stretched exponential or Kohlrausch function in relaxation theory [14] ; [15]. In Sections 2 ; 3, we develop the thermodynamic formalism of a classical stationary non-equilibrium system described by a power-law density admitting subexponential Weibull decay. In Sections 4 ; 5, we employ power-law densities with Weibull cutoff to perform a spectral fit to the all-particle cosmic-ray spectrum and to estimate the thermodynamic parameters of this relativistic nuclear gas.
Cosmic-ray nuclei can be treated as a classical gas, quantum corrections as well as the Coulomb interaction being negligible due to their low fugacity and density and high temperature. Relativistic statistical systems with short- and long-range interactions exhibiting quantum effects are studied in Refs. [16]; [17]; [18]; [19] ; [20] and references therein, pertaining to conceptual topics like negative heat capacities [16] and negative entropy [17] as well as to concrete applications such as astrophysical electron plasmas [18]; [19] ; [20]. Astro- and geophysical applications of sub- and superexponential Weibull factors (stretched and compressed exponentials with shape parameters σ<1 and σ>1, respectively) include asteroid fragmentation statistics [21], speed distributions of planetary surface winds [22]; [23] ; [24] and earthquake interevent times [25]; [26] ; [27]. Examples of network applications of the Weibull distribution can be found in Refs. [28]; [29]; [30] ; [31], ranging from traffic flows to market volatility. The original use of the Weibull distribution as empirical fracture probability of brittle solids is discussed in Refs. [32] ; [33]. A deformation of the Weibull density interpolating between the stretched exponential distribution and Pareto power laws [34] was used in Ref. [35] to model income distributions. Applications thereof in reliability modeling and weakest link theory are discussed in Refs. [36] ; [37]. Multi-parameter exponential densities with Pareto tails were also employed in Ref. [38] to model wealth distributions etc.
In the following, we give an outline of this paper. In Section 2, we study the entropy of a stationary non-equilibrium gas (classical, relativistic) defined by a spectral number density composed of a multiply broken power law and a Weibull exponential. Comparing with the entropy function of an equilibrium system, there are two major differences. The contribution U∕T of the internal energy to the entropy functional is replaced by the Weibull entropy accounting for the subexponential spectral decay, and the power-law factor in the number density describing the spectral breaks gives rise to an additional term in the entropy functional, the excess entropy which vanishes in an equilibrium system. Integral representations of Weibull and excess entropy suitable for numerical evaluation are also provided in Section 2. We also sketch the derivation of the spectral number density from the probability distribution in phase space, and derive excess entropy, Weibull entropy and total entropy as phase-space expectation values, the latter in −kBPlogP representation where P is the phase-space probability. We also briefly consider phase-space fluctuations of a stationary non-equilibrium gas, and show how to express the variances, covariances and higher-order correlations of the various thermodynamic variables by derivatives of the partition function. Like in an equilibrium system, the relative fluctuations vanish in the thermodynamic limit.
In Section 3,
we make use of the entropy variable to define the effective temperature
of a stationary non-equilibrium gas. As the Boltzmann factor is
replaced by the Weibull exponential and also because of the power-law
factor in the spectral number density, the cutoff temperature kBT in the Weibull exponential differs from the effective gas temperature defined as the reciprocal energy derivative of entropy, Teff=1∕S,U. The effective chemical potential is obtained in like manner as entropy derivative with respect to the number count, μeff=−S,N∕βeff. We also find the explicit relation βeff(β) between the effective temperature and the cutoff temperature in the Weibull factor, in terms of the temperature parameters βeff=1∕(kBTeff) and β=1∕(kBT)σ, where σ
is the Weibull spectral index. Another basic difference compared to an
equilibrium system is the pressure variable, which is unrelated to the
partition function (unlike in equilibrium, where βPV=logZ
holds) and has to be assembled from the spectral number density, the
particle momentum and the particle speed. We relate the pressure
variable to the effective temperature, to obtain the thermal equation of
state, and also derive the caloric equation relating the internal
energy to Teff. The isochoric and isobaric heat capacities are derived from the entropy variable, and we show that the inequalities 0<CV<CP are equivalent to a positive effective temperature parameter with positive derivative ![]() .
Subject to the same conditions, the isobaric expansion coefficient is
positive, and the isothermal and adiabatic compressibilities satisfy 0<κS<κTeff. To summarize Section 3,
we study the entropy function of a stationary non-equilibrium gas in
various parametrizations, derive numerically tame integral
representations of the thermodynamic variables, and discuss positivity
properties and thermodynamic inequalities relating to subexponential
spectral decay.
.
Subject to the same conditions, the isobaric expansion coefficient is
positive, and the isothermal and adiabatic compressibilities satisfy 0<κS<κTeff. To summarize Section 3,
we study the entropy function of a stationary non-equilibrium gas in
various parametrizations, derive numerically tame integral
representations of the thermodynamic variables, and discuss positivity
properties and thermodynamic inequalities relating to subexponential
spectral decay.
In Section 4, we perform spectral fits to the all-particle cosmic-ray spectrum, employing the spectral densities discussed in Sections 2 ; 3. The nuclei constituting the all-particle flux can roughly be divided into a light component of protons and helium, an intermediate-mass component of nitrogen-like nuclei, and a heavy iron-like component. In the 1GeV−104GeV range, the spectrum consists almost entirely, up to a fraction of one percent, of protons and helium nuclei. The proton and helium fluxes in this energy range have been measured by the Alpha Magnetic Spectrometer (AMS-02) on the International Space Station [1] ; [2] and by the balloon-borne CREAM experiment [3]. In the 105GeV−1011GeV interval, the mass composition is not yet known, although there exist some preliminary qualitative studies [6] ; [9]. This is the ultra-relativistic regime, where the nuclear mass becomes negligible compared to the particle energy. The all-particle spectrum, irrespectively of the nuclear mass composition, has been measured in this energy range by several ground-based experiments employing Cherenkov counters and fluorescence and scintillator detectors, such as Tibet-III [4], IceTop-73 [5] ; [6], KASCADE-Grande [7], Auger [8] and Telescope Array [9].
We first perform spectral fits to the AMS-02 proton and helium spectra in the 1GeV–104GeV interval. The all-particle spectrum in this interval can be approximated by adding the proton and helium fluxes. We then analytically extend the low-energy proton and helium fluxes into the 105GeV−1011GeV interval and perform a separate fit to the all-particle spectrum in this energy range. At energies above 104GeV, heavier nuclei can be accommodated in the extended proton and helium components, as the nuclear mass drops out of the flux density in this ultra-relativistic regime. The nuclear gas can thus be treated as a two-component mixture: In the 1GeV−104GeV interval, the flux density depends on the proton and helium (alpha particle) mass, and it becomes mass independent in the 104GeV−1011GeV interval. The all-particle flux can therefore be represented, over the complete 1GeV−1011GeV spectral range, as the sum of two partial fluxes (one depending on the proton mass and one on the helium mass), which are defined by multiply broken power-law densities with the same subexponential spectral cutoff exp(−(E∕(kBT))σ). The cutoff temperature inferred from the spectral fit is kBT=(2.5±0.1)×1010GeV, and the Weibull index is σ=0.66±0.02, so that the spectral decay substantially deviates from an exponential Boltzmann cutoff.
To obtain the thermodynamic parameters of the all-particle cosmic-ray spectrum, we need to generalize the formalism developed in Section 3 to cover a multi-component gas mixture, owing to the different particle masses. It suffices to consider a two-component mixture, as the flux density only depends on the hydrogen and helium mass at low energy and is mass independent in the ultra-relativistic regime. The thermodynamics of a two-component mixture in stationary non-equilibrium is elaborated in Section 5. First, we extract the spectral number densities of the gas components from the two partial fluxes constituting the all-particle flux. Then we assemble the entropy variable of this non-equilibrated mixture and calculate the effective gas temperature, kBTeff≈16GeV, from the energy derivative of entropy. In an equilibrium system, this temperature would coincide with the cutoff temperature in the Boltzmann factor. Because of the multiply broken power-law function in the spectral densities and the subexponential spectral decay, the cutoff temperature kBT≈2.5×1010GeV in the Weibull factor greatly differs from the actual gas temperature Teff. We also determine the effective chemical potentials of the gas components, derive the thermal and caloric equations of state, and give estimates of the internal energy and pressure of cosmic-ray nuclei. As done in Section 3 for a one-component gas, we calculate the heat capacities and compressibilities of a two-component mixture in stationary non-equilibrium, and verify the inequalities 0<CV<CP and 0<κS<κTeff as well as the positivity of the expansion coefficient of the nuclear gas. In Section 6, we present our conclusions.
2. Entropy of a classical relativistic gas in stationary non-equilibrium
2.1. Subexponential spectral decay
We will study a relativistic gas in stationary non-equilibrium defined by the spectral number density [39] ; [40]
2.2. Weibull and excess entropies
To obtain integral representations of the thermodynamic variables, we employ a more general distribution function than stated in (2.1),
which defines the partition function

2.3. Weibull probability distribution in phase space
We start with the n-particle phase-space measure
where the spatial d3qk integrations range over a volume V and the d3pk integrations over momentum space. The n-particle probability density leading to the spectral number density (2.2) reads with the random variables n and The normalization constant Z in (2.11) is defined by where the summation is over the particle number n. The factorial accounts for indistinguishability, and s is the spin degeneracy. Z is the grand partition function which reads in spectral representation2.4. Excess entropy, Weibull entropy and total entropy as phase-space expectation values
Differentiation of logZ in (2.13) with respect to the parameters of the exponential bn(p) in (2.11) leads to representations of the various thermodynamic variables as phase-space averages. For instance, the Weibull entropy (2.7) is assembled in phase space as
with wn defined in (2.12). The expectation values of excess entropy H=〈hn〉, internal energy U=〈un〉, pressure PV=〈vn〉 and particle number N=〈n〉 are defined in like manner, all being taken at γ=1,δ=ε=0. Evaluating the factorizing integrals, we arrive at the spectral representations stated in (2.3) –(2.8). The entropy variable reads with random variable
In contrast to an equilibrium system, the probability distribution Pn(p) in (2.11) (taken at γ=1, δ=ε=0) does not maximize the entropy functional (2.15) subject to the particle number and internal energy constraints N=〈n〉 and U=〈un〉, see after (2.14). Only the equilibrium distribution defined by h(p)=1 and σ=1 in (2.1) maximizes the entropy functional (2.15). To see this, we consider the equilibrium distribution ![]() , where Zeq is defined as in (2.13) (with bn replaced by
, where Zeq is defined as in (2.13) (with bn replaced by ![]() ), so that
), so that ![]() is normalized to one. The constraints prescribing N=〈n〉 and U=〈un〉 are defined as in (2.14) with Pn replaced by
is normalized to one. The constraints prescribing N=〈n〉 and U=〈un〉 are defined as in (2.14) with Pn replaced by ![]() ; the equilibrium entropy Seq is defined as in (2.15), also with this replacement
; the equilibrium entropy Seq is defined as in (2.15), also with this replacement ![]() . As Pn and
. As Pn and ![]() satisfy the same constraints, namely N=〈n〉,U=〈un〉 and the normalization (2.13), we can also average the equilibrium entropy Seq over Pn instead of
satisfy the same constraints, namely N=〈n〉,U=〈un〉 and the normalization (2.13), we can also average the equilibrium entropy Seq over Pn instead of ![]() . That is, Seq can be defined by replacing PnlogPn in (2.15) by
. That is, Seq can be defined by replacing PnlogPn in (2.15) by ![]() instead of
instead of ![]() . Finally we consider the difference S−Seq, with S in (2.15) and Seq defined by
. Finally we consider the difference S−Seq, with S in (2.15) and Seq defined by ![]() , and apply the general logarithmic inequality
, and apply the general logarithmic inequality ![]() and the normalization (2.13) (valid for Pn as well as
and the normalization (2.13) (valid for Pn as well as ![]() ) to find S<Seq.
) to find S<Seq.
2.5. Variances, covariances and higher-order correlations: fluctuations in stationary non-equilibrium ensembles
We calculate the variances of the particle number 〈(Δn)2〉, Weibull entropy 〈(Δwn)2〉, excess entropy 〈(Δhn)2〉, pressure 〈(Δvn)2〉 and internal energy 〈(Δun)2〉, using the phase-space random variables in (2.12) and the shortcuts Δn=n−〈n〉,Δwn=wn−〈wn〉, etc. The variances ![]() , etc., are then obtained as second derivatives of logZ. For instance, 〈(Δn)2〉=(logZ),α,α and 〈(Δwn)2〉=(logZ),β,β, taken at γ=1, δ=ε=0. We note the pairs (Δn,α), (Δwn,β),(Δhn,γ),(Δvn,δ) and (Δun,ε), cf. (2.11), so that the variances and covariances like 〈ΔnΔwn〉=(logZ),α,β and 〈ΔwnΔhn〉=(logZ),β,γ
are obtained by differentiation with the respective parameters.
Higher-order correlations are assembled analogously, e.g. the
triple correlations 〈Δn(Δwn)2〉=−(logZ),α,β,β and 〈ΔunΔwnΔhn〉=−(logZ),ε,β,γ;
the minus sign arises in case of an odd number of factors. Spectral
representations of correlations suitable for numerical computation are
thus obtained by multiple differentiation of the partition function
, etc., are then obtained as second derivatives of logZ. For instance, 〈(Δn)2〉=(logZ),α,α and 〈(Δwn)2〉=(logZ),β,β, taken at γ=1, δ=ε=0. We note the pairs (Δn,α), (Δwn,β),(Δhn,γ),(Δvn,δ) and (Δun,ε), cf. (2.11), so that the variances and covariances like 〈ΔnΔwn〉=(logZ),α,β and 〈ΔwnΔhn〉=(logZ),β,γ
are obtained by differentiation with the respective parameters.
Higher-order correlations are assembled analogously, e.g. the
triple correlations 〈Δn(Δwn)2〉=−(logZ),α,β,β and 〈ΔunΔwnΔhn〉=−(logZ),ε,β,γ;
the minus sign arises in case of an odd number of factors. Spectral
representations of correlations suitable for numerical computation are
thus obtained by multiple differentiation of the partition function ![]() as in (2.3) –(2.8).
The heat capacities and compressibilities of a gas in stationary
non-equilibrium can be expressed by the expectation values in
Section 2.4, their variances, covariances and triple correlations, see the remarks after (3.28).
as in (2.3) –(2.8).
The heat capacities and compressibilities of a gas in stationary
non-equilibrium can be expressed by the expectation values in
Section 2.4, their variances, covariances and triple correlations, see the remarks after (3.28).
The entropy variance ![]() , with Δsn=sn−〈sn〉, is a linear combination of the above variances and covariances, since Δsn=αΔn+βΔwn+Δhn, cf. (2.16). We square this to find
, with Δsn=sn−〈sn〉, is a linear combination of the above variances and covariances, since Δsn=αΔn+βΔwn+Δhn, cf. (2.16). We square this to find

3. Effective temperature and Weibull spectral decay: Thermodynamics of a stationary non-equilibrium gas
3.1. (α,β,V) parametrization of thermodynamic variables
We define the partition factor z by a rescaling of logZ in (2.3) with the volume factor and the fugacity f=e−α,
taken at γ=1,δ=ε=0, so that z and its derivatives (denoted by a subscript comma, e.g., z,β,z,β,γ) only depend on the Weibull exponent β=1∕(kBT)σ. As in Section 2.5, we consider the pairs ((p2+m2)σ∕2,β),All thermodynamic variables can efficiently be expressed and calculated in terms of the partition factor and its derivatives. Particle number, internal energy and pressure read, cf. (2.3), (2.4) ; (2.5),
Weibull entropy, excess entropy and total entropy are assembled as, cf. (2.6), (2.7), (2.8) ; (2.9),
3.2. (β,V,N) parametrization of internal energy, pressure and entropy
We invert the first identity in (3.2), α=log(zV∕N), to find the (β,V,N) representation of internal energy and pressure as
and the entropy variable3.3. Entropy in (U,V,N) parametrization: effective temperature and effective chemical potential
To eliminate the temperature variable β in the (β,V,N) representation, we invert U=Nu(β) in (3.5), β=u−1(U∕N), to find, cf. (3.7),

In Section 5, we will obtain the effective temperature and the chemical potential from a spectral fit. Conceptually, it is also possible to infer these parameters by equilibration with a thermal system. For notational simplicity, we assume this reference system to be a free relativistic gas defined by number density (2.1) with h(p)=1 and σ=1. The entropy function and the variables of this thermometer system are labeled with a subscript of two: S2(U2,V2,N2), so that S2,U2=β2,S2,V2=β2P2 and S2,N2=α2, with chemical potential μ2=−α2∕β2 and thermal equation β2P2=N2∕V2.
We keep the particle numbers N and N2 constant. When equilibrating S(U,V,N) in (3.8) and S2(U2,V2,N2), we use as contact variables βeff=β2≕βc and P=P2. The total energy and volume are kept constant, U+U2=Utot,V+V2=Vtot. We thus find the equations S2,U(U,V,N)=βc and S2,U2(U2,V2,N2)=βc, and the pressure identity gives η(β(βc))N∕V=N2∕(βcV2) by way of the thermal equations, cf. (3.6). (In the thermal scale factor η(β), we have substituted β=β(βeff), which is the inversion of βeff(β), cf. (3.9).) Together with the conservation conditions U+U2=Utot and V+V2=Vtot, we obtain five equations to determine the variables U, U2, V, V2 and βc; the latter is a Lagrange parameter used to maximize S(U,V,N)+S2(U2,V2,N2) with respect to the energy variables subject to the constraint U+U2=Utot. The total entropy S+S2 is not maximized with respect to the volume variables V and V2, as this would require to equate P∕η(β(βc))=P2βc instead of the pressure variables, P=P2. Only if η(β(βc))=1∕βc, which happens if S(U,V,N) is an equilibrium entropy, the contact identity P=P2 amounts to maximize the total entropy S+S2 also with respect to the volume variables subject to V+V2=Vtot. This reflects the fact that the phase-space probability distribution Pn(p) in (2.11) does not maximize the entropy functional (2.15); only the equilibrium distribution ![]() gives the maximum entropy, see after (2.16). In brief, the stationary non-equilibrium entropy (3.4) is always smaller than the equilibrium entropy if subjected to the same constraints.
gives the maximum entropy, see after (2.16). In brief, the stationary non-equilibrium entropy (3.4) is always smaller than the equilibrium entropy if subjected to the same constraints.
3.4. Entropy in (βeff,V,N) parametrization, thermal and caloric equations of state, and isochoric heat capacity
We use the effective temperature parameter βeff=s′(β)∕u′(β) in (3.9) as independent variable, and substitute the inversion β=β(βeff) into the (β,V,N) representation in Section 3.2. The existence of this inversion is assured by the positivity conditions βeff(β)>0 and ![]() , see Section 3.8, but we will not need to perform it explicitly. The caloric and thermal equations of state read U=Nu(β(βeff)) and P=η(β(βeff))N∕V, cf. (3.5) ; (3.6), and the (βeff,V,N) representation of entropy is, cf. (3.7),
, see Section 3.8, but we will not need to perform it explicitly. The caloric and thermal equations of state read U=Nu(β(βeff)) and P=η(β(βeff))N∕V, cf. (3.5) ; (3.6), and the (βeff,V,N) representation of entropy is, cf. (3.7),



3.5. Internal energy in (S,V,N) parametrization
We invert S(β,V,N) in (3.7), solving for β,
to find, cf. (3.5), We note the derivatives U,S=1∕βeff,U,N=μeff, cf. ; (3.12), and U,V=−N∕(Vβeff).3.6. Entropy and volume in (βeff,P,N) parametrization: isobaric heat capacity, isothermal compressibility and isobaric expansion coefficient
By way of the thermal equation in Section 3.4, the volume can be parametrized as
The internal energy U=Nu(β(βeff)) reads as in Section 3.4, since it is independent of the volume factor. The entropy in (βeff,P,N) representation is obtained by eliminating the volume in (3.13) by substitution of (3.18), The βeff derivative thereof is with S,βeff(βeff,V,N) as in (3.14). The derivatives of η(β) in (3.6) and g(β) in (3.19) read, cf. ; (3.11), The isobaric specific heat CP=TeffS,Teff(βeff,P,N) can be read off from the entropy derivative in (3.20), In Section 3.8, we will show that CP>CV>0 follows from the positivity of βeff(β) andThe derivatives of the volume factor V(βeff,P,N) in (3.18),
define the isothermal compressibility, κTeff=−V,P∕V=1∕P, and the isobaric expansion coefficient, We also note CP=CV+Nαexp∕βeff, cf. (3.22). In equilibrium, αexp=βeff=β.3.7. Volume in (S,P,N) parametrization: adiabatic compressibility
We start with the entropy representation in (3.19) and solve for β,

In the energy density u(β) and the thermal scale factor η(β) in (3.5) ; (3.6), z can be replaced by logZ, as the volume factor and the fugacity f=e−α in (3.1) scale out. The same holds for the derivatives of u(β),s(β) and η(β) in (3.11), ; (3.21), so that they can be expressed by the expectation values and correlations derived in Sections 2. For instance, logZ=〈n〉,(logZ),β=−〈wn〉,(logZ),γ,β=〈ΔhnΔwn〉 and (logZ)ε,β,β=−〈Δun(Δwn)2〉. This also holds true for the effective temperature parameter βeff(β) and its derivative, cf. ; , as well as for the heat capacities (3.14) ; (3.22), the expansion coefficient (3.24) and the compressibilities in (3.28), as they are assembled from the mentioned quantities.
3.8. Positivity of heat capacity, compressibility and expansion coefficient
To discuss positivity properties, we need the Chebyshev integral inequality
whereThe energy density u(β)=−z,ε∕z defining the internal energy in (3.5) is positive, which follows from the integral representation of z and z,ε, cf. (3.1). The derivative u′(β) in (3.11) is negative, which follows from the Chebyshev inequality. A positive effective temperature βeff=s′(β)∕u′(β), cf. (3.9), is thus tantamount to a negative derivative s′(β); the first term of s′(β) in (3.11) is negative according to the Chebyshev inequality, but the second term can be positive and overpower the first term, since γ differentiation of z generates the factor logh(p) in the integrand of (3.1),
which is in general not a monotonic function so that the Chebyshev
inequality is not applicable. Positivity of the effective temperature βeff as well as a positive derivative ![]() are necessary and sufficient conditions for the thermodynamic
inequalities discussed below. In an equilibrium system, these conditions
are always satisfied, since βeff=β.
are necessary and sufficient conditions for the thermodynamic
inequalities discussed below. In an equilibrium system, these conditions
are always satisfied, since βeff=β.
The thermal scale factor η(β)=−z,δ∕z in (3.6) is positive, which follows from the integral representation of z and z,δ, cf. (3.1). Its derivative, η′(β) in (3.21) is negative according to the Chebyshev inequality. The heat capacities thus satisfy CP>CV>0, cf. (3.14) ; (3.22), if βeff>0 and ![]() . As for the compressibilities, the coefficient CR(β) in (3.28) defining the compressibility ratio is positive if βeff>0 (since η′(β)<0,u′(β)<0 and η(β)>0), so that the compressibilities satisfy 0<κS<κTeff.
. As for the compressibilities, the coefficient CR(β) in (3.28) defining the compressibility ratio is positive if βeff>0 (since η′(β)<0,u′(β)<0 and η(β)>0), so that the compressibilities satisfy 0<κS<κTeff.
To summarize, a necessary and sufficient condition for the inequalities CP>CV>0 to hold is a positive effective temperature parameter βeff with positive derivative ![]() . In particular, CV>0 is equivalent to
. In particular, CV>0 is equivalent to ![]() , and CP>CV is equivalent to
, and CP>CV is equivalent to ![]() . The inequalities 0<κS<κTeff with κTeff=1∕P are equivalent to βeff>0. A positive expansion coefficient αexp in (3.24) is equivalent to
. The inequalities 0<κS<κTeff with κTeff=1∕P are equivalent to βeff>0. A positive expansion coefficient αexp in (3.24) is equivalent to ![]() .
.
4. Weibull decay of the spectral flux density of ultra-high energy cosmic-ray nuclei
In Sections 2 ; 3, we have studied a general stationary non-equilibrium gas defined by a spectral number density dρ∕dp structured as in (2.1). Here and in the next section, we discuss a concrete example, cosmic-ray nuclei constituting a relativistic gas mixture in stationary non-equilibrium. The flux density of this nuclear gas, based on number density (2.1), can be inferred from a spectral fit. In this section, we will perform the spectral fit, using flux data collected by several recent experiments covering the 1GeV−1011GeV interval, cf. Section 1, and find an analytic representation of the flux density and in particular of the power-law spectral function h(p) in number density (2.1) which has been left unspecified so far.
The differential flux density per steradian defined by number density dρ∕dp in (2.1) is dΦ∕dp=υdρ∕(4πdp), with group velocity υ=p∕E and dispersion relation ![]() . The spectral fit is performed with the rescaled flux density F=pκdΦ∕dp, cf. (2.1),
. The spectral fit is performed with the rescaled flux density F=pκdΦ∕dp, cf. (2.1),
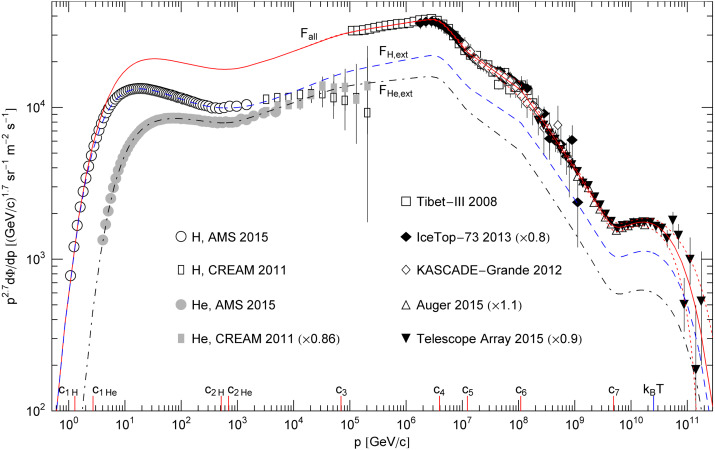
The all-particle flux density Fall of the nuclear gas in Fig. 1 is fitted with two partial fluxes of type (4.1), Fall=FH,ext+FHe,ext,
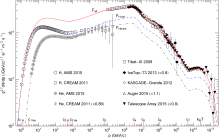
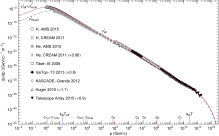
where the spectral kernel hH,ext is a multiply broken power law with smooth transitions at the spectral breaks, The second flux component FHe,ext and its spectral kernel hHe,ext are defined analogously, with the H subscript replaced by He. The positive amplitudes ck (indexed in ascending order) in (4.4) determine the location of the spectral breaks, see Fig. 1 ; Fig. 2. The exponents γk and δk are positive as well; the γk define the slopes of the spectral curve between the spectral breaks (which are nearly straight in double-logarithmic plots), and the δk determine the curvature of the spectral map at the spectral breaks ck. The exponents and amplitudes of the spectral functions hH,ext and hHe,ext obtained from the χ2 fit are recorded in Table 1.The power-law function (4.4) is an example of how wideband spectra exhibiting extended spectral slopes and multiple spectral breaks [45]; [46]; [47]; [48] ; [49] can systematically be assembled. First, one visually determines the approximate location of the spectral breaks ck in a double-logarithmic plot of the data sets. (The break points ck are the joints of spectral slopes, as indicated on the abscissa of Fig. 1 ; Fig. 2.) These preliminary ck are used as initial guess in the least square fit, and they determine the number of factors in the spectral function ∏k(1+(p∕ck)γk∕|δk|)δk. (In this product notation, we use negative exponents δk for the factors in the denominator of (4.4).) Initial guesses for the exponents γk and the sign of δk can be read off from the ascending or descending spectral slopes. A moderate exponent δk results in a gradual change of the slope at the spectral break ck, and a δk close to zero causes a sudden break in the spectral map. Each spectral break is thus determined by three parameters, the location of the break points ck, the power-law index γk of one adjacent slope, and the curvature exponent δk. The power-law function (4.4) describes seven spectral breaks specified by 21 parameters. To locate the spectral breaks in the flux map, it is also necessary to rescale the flux data, to make the spectral fine structure visible. This is done in Fig. 1 ; Fig. 2 by multiplying the spectral flux density by a factor of p2.7. In the unscaled flux representation of Fig. 3, which is also a log–log plot, the fine structure is largely concealed.
The partial flux FH,ext(p) in (4.3) is the extension of the low-energy (1GeV–104GeV) hydrogen component of the all-particle spectrum defined by the AMS-02 [1] ; [2] and CREAM [3] hydrogen flux points in Fig. 1,
Analogously, FHe,ext is the extension of the low-energy helium flux FHe, low defined by the AMS-02 and CREAM helium flux points in Fig. 1; FHe, low(p) is parametrized as in (4.5), with the H subscript replaced by He. We use mH≈0.938GeV as proton mass and mHe≈3.727GeV for alpha particles. The amplitudes AΦ,H and AΦ,He in (4.3) ; (4.5) are related to the fugacity parameters αH and αHe as stated in (4.2), with spin degeneracy sH=2 for protons and sHe=1 for alpha particles. In the Weibull factor in (4.3), we can drop the mass term, using exp(−βpσ) instead, as the spectral cutoff happens at very high momentum in the ultra-relativistic regime where the nuclear mass is negligible, see the spectral cutoff depicted in Fig. 2. The amplitudes AΦ,H and AΦ,He as well as the decay exponent β=1∕(kBT)σ and the spectral index σ of the Weibull factor, cf. Section 2.1, are fitting parameters listed in Table 2.The spectral fit is performed in two steps. First, we fit the hydrogen and helium components, in the low-energy interval from 1GeV to 104GeV, using the AMS-02 and CREAM data sets and the low-energy limit (4.5). In this way, we obtain the flux amplitude AΦ,H, the power-law amplitudes c1H,c2H and the exponents γ1H,γ2H and δ1H,δ2H, and analogously for the helium fit. In the 1GeV–104GeV interval, the all-particle flux consists mainly of hydrogen and helium nuclei; heavier nuclei contribute only around one percent to the total flux in this interval, so that the all-particle flux in this energy range can be approximated by Fall∼FH,low+FHe,low.
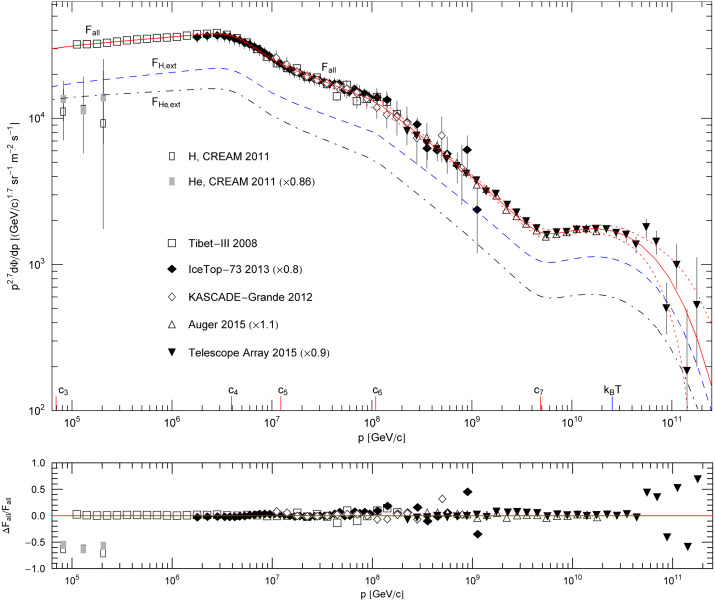
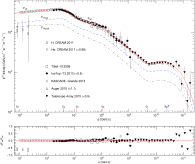
The second step is to fit the high-energy all-particle spectrum in the 105GeV−1011GeV interval as defined by the Tibet-III [4], IceTop-73 [5] ; [6], KASCADE-Grande [7], Auger [8] and Telescope Array [9] flux points in Fig. 1 ; Fig. 2. To this end, we extend the low-energy fit FH,low+FHe,low to higher energies, by adding power-law factors to the spectral kernels hH,low(p) and hHe,low(p) as done in (4.4). The added power-law factors are the same for both kernels, with amplitudes ck=3,…,7 and exponents γk,δk listed in Table 1. The high-energy flux extensions FH,ext and FHe,ext above 104GeV also contain heavier nuclei, an intermediate-mass nitrogen-like component and a heavy iron-like component. At ultra-relativistic energies above 104GeV, the nuclear rest mass is negligible since m2∕p2≪1, so that heavier nuclei can be accommodated in the hydrogen and helium flux extensions. The spectral breaks ck indicated on the abscissa of Fig. 1 ; Fig. 2 are clearly discernible in the total flux Fall=FH,ext+FHe,ext and the partial fluxes. The Weibull factor with spectral index σ=0.66±0.02 in flux density (4.3) generates the subexponential spectral cutoff in the ultra-high energy regime above the ‘ankle’ c7≈4.9×109GeV of the all-particle spectrum, cf. Fig. 2; another major spectral break occurs at the ‘knee’ c4≈3.9×106GeV, cf. Refs. [10] ; [50].
5. Cosmic-ray nuclei: a relativistic gas mixture in stationary non-equilibrium
5.1. Reduction to a two-component mixture: spectral extension of the low-energy hydrogen and helium components
The following discussion is a step-by-step adaptation of the thermodynamic formalism developed in Section 3 (for a one-component gas in stationary non-equilibrium) to cosmic-ray nuclei, which constitute a gas mixture because of the different particle masses. In Section 4, we have represented the empirical flux density of the all-particle cosmic-ray spectrum as the sum of two partial fluxes, Fall=FH,ext+FHe,ext, which are extensions of the low-energy hydrogen and helium fluxes, cf. (4.3) ; (4.5). Heavier nuclei have been included in these two extensions, since the all-particle spectrum below 104GeV is predominantly composed of protons and helium, and above 104GeV, the flux densities are mass independent. In effect, the all-particle flux density Fall depends only on the proton and helium mass, and can therefore be treated as a two-component mixture.
As pointed out after (4.2), the differential number density dρH,ext can be inferred from the flux density FH,ext (obtained from the spectral fit described in Section 4, cf. (4.3) ; (4.4) and Table 1 ; Table 2),
The partition function defined by this number density isAs in Section 3.1, the partition factor of the hydrogen spectral extension dρH,ext is defined by
with spectral measure, cf. (2.2) ; (3.1), hH,ext(p) is the power-law spectral function (4.4), mH the proton mass and sH the spin degeneracy, cf. after (4.5). The partition factor zH and derivatives thereof are taken at γ=1,δ=ε=0, see Section 3.1, so that zH only depends on the decay exponent β. At γ=1,δ=ε=0, we findThe number count, internal energy and pressure of the hydrogenic partial flux FH,ext can thus be calculated as NH=Ve−αHzH,UH=−Ve−αHzH,ε,PH=−e−αHzH,δ, and the Weibull and excess entropies read WH∕β=−Ve−αHzH,β and HH=−Ve−αHzH,γ, cf. Section 2.2; αH is the fugacity parameter of the hydrogen component. This also holds for the helium extension FHe,ext with subscript H replaced by He in (5.2) ; (5.3). The respective quantities of the all-particle flux Fall are obtained by addition, N=NH+NHe, W=WH+WHe, etc. In this way, we find the (αH,αHe,β,V) parametrization of the thermodynamic variables. The entropy is assembled as S(αH,αHe,β,V)=SH+SHe, where, cf. (3.4),

When calculating thermodynamic variables from spectral fits, the (α,β,V) parametrization is the most efficient representation. The variables N,U,S,W,H and P listed in the first row of Table 3 are assembled as stated after (5.3). The partition factor zH in (5.2) and its derivatives, cf. after (3.1), are calculated with the spectral measure ![]() obtained from the hydrogenic flux extension FH,ext by way of (5.1). The analytic flux density FH,ext is stated in (4.3) ; (4.4), with fit parameters in Table 1 ; Table 2. The fugacity fH is calculated from the flux amplitude in (4.2) and Table 2. Analogously for the partition factor zHe of the helium component.
obtained from the hydrogenic flux extension FH,ext by way of (5.1). The analytic flux density FH,ext is stated in (4.3) ; (4.4), with fit parameters in Table 1 ; Table 2. The fugacity fH is calculated from the flux amplitude in (4.2) and Table 2. Analogously for the partition factor zHe of the helium component.
5.2. Thermal equation of state of a stationary non-equilibrium mixture
To obtain the thermodynamic variables in (β,V,NH,NHe) parametrization, we invert the number count, αH=log(zHV∕NH), and substitute the fugacity parameter αH, cf. after (5.3). The hydrogen component of the internal energy then reads
and analogously the helium component UHe(β,NHe). The total internal energy of the mixture is thus The partial pressures and the thermal equation of state read The entropy variable S(β,V,NH,NHe) is assembled as where sH(β) and sHe(β) are defined in (3.7), with the partition factor z indexed zH and zHe, respectively.5.3. Effective temperature and chemical potential of cosmic-ray nuclei
To calculate the effective gas temperature, we need the (U,V,NH,NHe) parametrization of entropy. Inversion of the internal energy in (5.6) and substitution of ![]() into (5.8) gives
into (5.8) gives
5.4. Caloric equation of state and isochoric heat capacity of the nuclear gas
We switch to the (βeff,V,NH,NHe) parametrization. By inverting βeff in (5.10), β=β(βeff,NH,NHe), and substituting into (5.6), we find the caloric equation of state
We also note the thermal equation in this representation, cf. (5.7), and the entropy, cf. (5.8), The isochoric heat capacity CV=TeffS,Teff(βeff,V,NH,NHe) reads The β derivative of the effective temperature parameter βeff(β,NH,NHe) is assembled as with βeff and5.5. Isobaric heat capacity, isothermal compressibility and isobaric expansion coefficient of the nuclear gas
The (βeff,P,NH,NHe) parametrization is used in this section. By way of the thermal equation (5.13), we find the volume factor V(βeff,P,NH,NHe). The internal energy U(βeff,NH,NHe) in (5.12) remains unchanged, as it does not depend on the volume factor. The entropy S(βeff,P,NH,NHe) is found by eliminating V in (5.14) via the thermal equation,
The βeff derivative thereof reads with S,βeff(βeff,V,NH,NHe) as in (5.15). We also note the derivatives withThe βeff and P derivatives of the volume factor V(βeff,P,NH,NHe) in (5.13),
define the isothermal compressibility κTeff=−V,P∕V=1∕P, cf. Table 3, and the isobaric expansion coefficient, which is positive if βeff,β(β,NH,NHe)>0. The expansion coefficient is calculated via (5.23) and listed in Table 3. In equilibrium,5.6. Adiabatic compressibility of a gas mixture in stationary non-equilibrium
To obtain the (S,P,NH,NHe) parametrization of the volume factor, we solve the entropy function S(β,P,NH,NHe) in (5.17) for β,
and substitute this into the thermal equation (5.7), The pressure derivative thereof is with the derivatives6. Conclusion
The measured all-particle cosmic-ray flux is highly isotropic and stationary, which suggests to treat the relativistic nuclei as a classical stationary non-equilibrium gas. Quantum effects and the Coulomb interaction can be discounted due to the low density and high temperature. The all-particle flux has been measured with good precision over an extended energy range, from 1 GeV up to 1011GeV, so that even minor spectral breaks can be located in suitably rescaled flux maps, see Fig. 1 ; Fig. 2. The multiply broken power-law distribution and the Weibull factor defining the spectral cutoff can be extracted from the flux data by way of a least-squares fit. The ultra-high energy spectral tail above 1010GeV, measured with fluorescence and scintillation counters of the Telescope Array, exhibits subexponential decay and permits to infer the cutoff temperature and the decay exponent σ of the Weibull factor exp(−(E∕(kBT))σ) quite accurately, cf. Table 2.
The multiply broken power-law distribution and the Weibull cutoff (setting in at about kBT≈2.5×1010GeV) determine the spectral number density of the nuclear gas. This density is the basis for the thermodynamic formalism developed here and can empirically be reconstructed from available flux data, cf. Fig. 3. This does not require to make specific assumptions about the driving forces generating the stationary non-equilibrium, the production, acceleration, scattering and absorption mechanisms cosmic-ray nuclei undergo, which are uncertain and would have to be specified in ab initio calculations based on kinetic equations. Currently contemplated production sites of cosmic-ray nuclei are Galactic supernova remnants and, in the case of ultra-high energy cosmic rays, active galactic nuclei [10]. The evidence for that is circumstantial, mainly from TeV gamma-ray spectra of a limited number of supernova remnants which can be explained by a radiation model involving high-energy protons. This model assumes gamma-ray emission by pion decay, the pions being produced in collisions of high-energy protons with heavier nuclei. High-energy protons can be produced by shock acceleration in supernova blast waves. The caveat here is that TeV gamma-rays can also be generated by inverse Compton scattering and tachyonic radiation processes [51], which do not require high-energy nuclei. The decay of the all-particle spectrum above 1010GeV, cf. Fig. 2, could be caused by scattering of protons by cosmic microwave background photons, resulting in energy loss by pion production. Other attenuation mechanisms at high energy could be electron–positron pair production and photo-disintegration of heavy nuclei by interaction with the extragalactic background light. As it is presently not possible to quantify the production and absorption mechanisms, we have refrained from ab initio kinetic theory and extracted the number density of the nuclear gas from empirical spectra, cf. Section 4. To systematically model the fine structure of a multiply broken wideband spectrum requires a large number of parameters, as exemplified by the power-law function (4.4), which contains seven spectral breaks, cf. Table 1 and Fig. 1 ; Fig. 2. Ab initio calculations of the all-particle wideband have not been attempted yet, although some of the mentioned acceleration and attenuation mechanisms have been tested in various energy ranges [10]; [52] ; [53].
Apart from the specific example of cosmic-ray nuclei studied in Sections 4 ; 5, we developed the thermodynamics of a classical stationary non-equilibrium gas (of relativistic particles) defined by a power-law distribution with Weibull spectral cutoff. In Section 2, we introduced the number density and the entropy functional, at first in spectral representation and then in relativistic phase space. The entropy functional substantially differs from an equilibrium entropy, as the multiply broken power law in the spectral number density generates excess entropy absent in an equilibrium system, and the Weibull entropy replaces the contribution of the internal energy to the entropy functional. In fact, Weibull entropy is quite unrelated to internal energy and only happens to coincide with U∕T at spectral index σ=1 where the Weibull exponential coincides with the Boltzmann factor, see (2.7). The spectral representation of the thermodynamic variables stated in Section 2 is suitable for numerical evaluation once the number density has been specified by a spectral fit; their phase-space representation is also derived in Section 2.
In Section 3, we invoked the entropy variable to define the effective temperature of a gas in stationary non-equilibrium and established the relation βeff(β) between the effective gas temperature βeff=1∕(kBTeff) and the cutoff temperature β=1∕(kBT)σ in the Weibull exponential. We then derived the heat capacities and compressibilities of a stationary non-equilibrium gas and discussed thermodynamic inequalities such as 0<CV<CP, relating them to the positivity of the effective temperature parameter βeff(β) and its derivative.
Cosmic-ray nuclei constitute a multi-component gas mixture because of the different particle masses. In Section 4, we represented the flux density of the all-particle spectrum as a two-component mixture composed of extended hydrogen and helium fluxes, Fall=FH,ext+FHe,ext, cf. Fig. 1 ; Fig. 2. This reduction to a two-component system is possible as the low-energy spectrum consists almost exclusively of protons and helium nuclei and, above 104GeV, the spectral density becomes ultra-relativistic so that the nuclear mass drops out and heavier nuclei can be accommodated in the hydrogen and helium flux components. In Section 5, we adapted the thermodynamic formalism developed in Section 3 to a two-component mixture and applied it to cosmic-ray nuclei. We extracted the partial number densities dρH,ext/dp and dρHe,ext/dp of the nuclear gas (see Fig. 3) from the flux densities FH,ext,FHe,ext obtained from a least-squares fit to the all-particle spectrum, cf. Section 4 and Fig. 1 ; Fig. 2. Finally we substituted the partial number densities into the spectral representations of the thermodynamic variables, cf. Section 2, to estimate the thermodynamic parameters of cosmic-ray nuclei: effective temperature, internal energy, pressure and entropy, as well as the heat capacities, the expansion coefficient and the isothermal and adiabatic compressibility of this non-equilibrated gas mixture, see Table 3.
- Fig. 1.
Spectral fit to the all-particle flux of cosmic-ray nuclei in the 1GeV−1011GeV interval. Data points from AMS-02 [1] ; [2], CREAM [3], Tibet-III [4], IceTop-73 (rescaled by a factor of 0.8) [5] ; [6], KASCADE-Grande [7], Auger (rescaled by 1.1) [8] and Telescope Array (rescaled by 0.9) [9]. The rescaling is needed to obtain a continuous spectral curve. First, two independent χ2 fits are performed to the hydrogen and helium flux points in the 1GeV−104GeV interval with the low-energy flux densities FH, low and FHe, low in (4.5) (χ2(H)∕dof≈15.1∕68,χ2(He)∕dof≈12.2∕66). An approximation of the total flux is obtained by adding the hydrogen and helium fluxes, as the all-particle spectrum in this energy range consists predominantly of hydrogen and helium, Fall, low=FH, low+FHe, low. The flux density Fall, low is then analytically extended to higher energies as a multiply broken power law with Weibull spectral cutoff, Fall=FH,ext+FHe,ext, cf. (4.3) ; (4.4), and a separate least-squares fit is performed to the all-particle flux points in the 105GeV−1011GeV interval with flux density Fall (solid curve, χ2∕dof≈212∕102). Also depicted are the partial fluxes FH,ext and FHe,ext (dashed and dot-dashed curves, respectively), which are analytic extensions of the low-energy fluxes FH, low and FHe, low in the 1GeV−104GeV interval, cf. (4.3) –(4.5). The dotted curves define the 3σ error band, better visible in Fig. 2. The fit parameters of the all-particle flux Fall are listed in Table 1 ; Table 2. The clearly visible spectral breaks (labeled ck in Table 1) are indicated on the abscissa, as well as the cutoff temperature kBT in the Weibull factor of the flux density, cf. (4.3).
- Fig. 2.
Subexponential Weibull decay of the all-particle cosmic-ray spectrum. This is a close-up of Fig. 1; data points as in Fig. 1. Below the cutoff energy at kBT≈2.5×1010GeV, the flux density Fall (solid curve) is composed of multiple power-law segments (appearing approximately straight in log–log plots) with smooth transitions at the spectral breaks ck, cf. Table 1. The subexponential spectral decay at ultra-high energies above kBT is caused by the Weibull factor exp[−(p∕(kBT))σ] in flux density (4.3). The spectral index is σ≈0.66, cf. Table 2, resulting in subexponential decay. The extensions FH,ext and FHe,ext (dashed and dot-dashed curves) of the low-energy hydrogen and helium fluxes, cf. the caption to Fig. 1, contain admixtures of heavier nuclei (in the ultra-relativistic regime above 104GeV) and add up to the all-particle flux, Fall=FH, ext+FHe,ext, cf. (4.3) ; (4.4). The 3σ error band is indicated by the dotted curves. The residuals of the least-squares fit of Fall are shown in the lower panel.
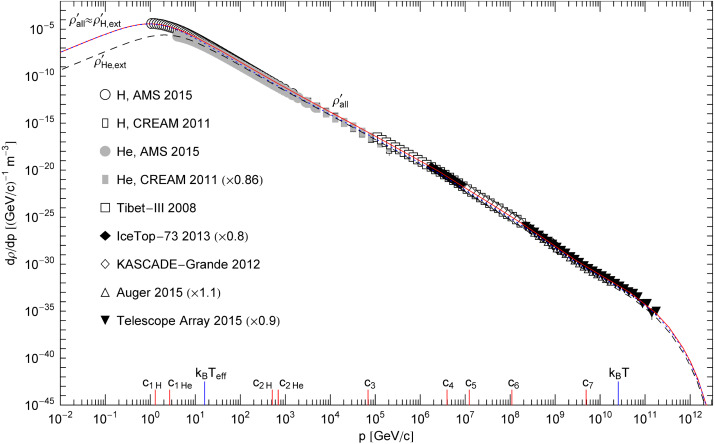
- Fig. 3.
Spectral number density of cosmic-ray nuclei. Data points as in Fig. 1. The differential number density dρall/dp (solid curve
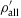 ) of the nuclear gas is the sum of two partial densities,
) of the nuclear gas is the sum of two partial densities, 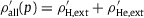 ; the scale factor p2.7 used in the plots of the corresponding partial fluxes FH, ext and FHe, ext in Fig. 1 ; Fig. 2 has been dropped in this figure. As the helium extension
; the scale factor p2.7 used in the plots of the corresponding partial fluxes FH, ext and FHe, ext in Fig. 1 ; Fig. 2 has been dropped in this figure. As the helium extension 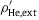 (dashed curve) is by about one order lower than the hydrogen extension
(dashed curve) is by about one order lower than the hydrogen extension 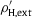 (dotted), the total density
(dotted), the total density 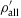 is nearly indistinguishable from
is nearly indistinguishable from 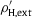 in this unscaled representation. The partial number densities
in this unscaled representation. The partial number densities 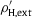 ,
, 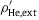 are extracted from the flux densities FH, ext, FHe, ext in Fig. 1 ; Fig. 2 by way of Eq. (5.1). In the interval between the spectral peak and the subexponential spectral cutoff at kBT≈2.5×1010GeV,
the number density appears as nearly straight power-law slope in this
representation, despite of multiple spectral breaks indicated on the
abscissa. Discounting these breaks,
are extracted from the flux densities FH, ext, FHe, ext in Fig. 1 ; Fig. 2 by way of Eq. (5.1). In the interval between the spectral peak and the subexponential spectral cutoff at kBT≈2.5×1010GeV,
the number density appears as nearly straight power-law slope in this
representation, despite of multiple spectral breaks indicated on the
abscissa. Discounting these breaks, 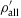 has a simple structure: a power-law ascent, a spectral peak at around 1GeV, an extended power-law descent, and a subexponential spectral tail above the cutoff temperature kBT. Also indicated on the abscissa is the effective temperature kBTeff≈16GeV of the nuclear gas, cf. (5.10) and Table 3.
has a simple structure: a power-law ascent, a spectral peak at around 1GeV, an extended power-law descent, and a subexponential spectral tail above the cutoff temperature kBT. Also indicated on the abscissa is the effective temperature kBTeff≈16GeV of the nuclear gas, cf. (5.10) and Table 3.
- Table 1.
Fitting parameters of the spectral functions hH,ext(p) and hHe,ext(p) of the extended hydrogen and helium fluxes FH,ext,FHe,ext in Fig. 1 ; Fig. 2. The spectral functions are multiply broken power laws stated in (4.4). The power-law amplitudes ck define the location of the spectral breaks, see Fig. 1. The exponents γk determine the spectral slopes between the breaks, and the exponents δk the spectral curvature at the break points.
k ck[GeV/c] γk δk 1H 1.283 4.910 4.125 2H 5.128×102 0.3709 0.3698 1He 2.694 4.775 3.848 2He 6.955×102 0.2045 6.409×10−2 3 6.925×104 8.857×10−2 3.091×10−2 4 3.935×106 0.5185 8.622×10−2 5 1.227×107 0.2067 3.182×10−3 6 1.091×108 0.2463 2.193×10−3 7 4.866×109 0.9946 0.1957 - Full-size table
- Table 2.
Flux amplitudes and decay parameters. AΦ,H and AΦ,He denote the amplitudes of the partial fluxes FH,ext,FHe,ext in (4.3). The subexponential spectral decay of the flux components is determined by the Weibull factor exp(−βpσ), where σ is the spectral index and β the decay exponent related to the cutoff temperature by β=1∕(kBT)σ. (The mass-square in the Weibull factor in (4.3) can be dropped because of the high cutoff temperature.)
AΦ,H[(GeV/c)−3sr−1m−2s−1] AΦ,He[(GeV/c)−3sr−1m−2s−1] kBT[GeV] σ β[GeV−σ] (8.428±1.6)×103 (1.095±0.20)×102 (2.529±0.070)×1010 0.6645±0.014 1.223×10−7 - Full-size table
- Table 3.
Thermodynamic parameters of the all-particle spectrum of cosmic-ray nuclei, a relativistic gas mixture in stationary non-equilibrium. The spectral number density of the nuclei is depicted in Fig. 3. Recorded in the first row: particle count N, internal energy U, total entropy S, Weibull entropy W, excess entropy H, pressure P, isochoric heat capacity CV, and isobaric heat capacity CP. These quantities are listed as specific densities rescaled with the volume factor and the Boltzmann constant kB. The calculation of the variables N,U,S,W,H and P is explained in Section 5.1. The heat capacities CV and CP are assembled as stated in (5.15) ; (5.21). Quantities recorded in the second row: isothermal compressibility κTeff, cf. after (5.22), adiabatic compressibility κS, cf. (5.27), heat capacity ratio CP∕CV coinciding with the compressibility ratio κTeff∕κS, cf. after (5.27), isobaric expansion coefficient αexp, cf. (5.23), effective temperature parameter βeff=1∕(kBTeff), cf. (5.10), effective temperature Teff, and the equipartition ratio U∕(NkBTeff).
N∕V[m−3] U∕V[GeV m−3] S∕(kBV)[m−3] W∕(kBV)[m−3] H∕(kBV)[m−3] P[GeV m−3] CV∕(kBV)[m−3] CP∕(kBV)[m−3] 1.238×10−4 5.935×10−4 1.490×10−2 3.741×10−11 5.937×10−4 1.705×10−4 6.271×10−9 3.083×10−8 κTeff[GeV−1 m3] κS[GeV−1 m3] CP∕CV, κTeff∕κS αexp∕kB[GeV−1] βeff[GeV−1] kBTeff[GeV] Teff[K] U∕(NkBTeff) 5.866×103 1.193×103 4.915 1.233×10−5 6.216×10−2 16.09 1.867×1014 0.2981 - Full-size table
References
- [1]
Phys. Rev. Lett., 114 (2015), p. 171103
- [SD-008]
- [2]
Phys. Rev. Lett., 115 (2015), p. 211101
- [SD-008]
- [3]
Astrophys. J, 728 (2011), p. 122
- [SD-008]
- [4]
Astrophys. J, 678 (2008), p. 1165
- [SD-008]
- [5]
Phys. Rev. D, 88 (2013), p. 042004
- [SD-008]
- [6]
Proc. Sci. (2015) PoS(ICRC2015)334
- [SD-008]
- [7]
Astropart. Phys., 36 (2012), p. 183
- [SD-008]
- [8]
Proc. Sci. (2015) PoS(ICRC2015)271
- [SD-008]
- [9]
Proc. Sci. (2015) PoS(ICRC2015)035
- [SD-008]
- [10]
Rev. Modern Phys., 83 (2011), p. 907
- [SD-008]
- [11]
Annu. Rev. Astron. Astrophys., 53 (2015), p. 199
- [SD-008]
- [12]
J Appl. Mech., 18 (1951), p. 293
- [SD-008]
- [13]
- [SD-008]
- [14]
Physica A, 392 (2013), p. 1153
- [SD-008]
- [15]
Physica A, 391 (2012), p. 3446
- [SD-008]
- [16]
Physica A, 263 (1999), p. 293
- [SD-008]
- [17]
Phys. Life Rev., 5 (2008), p. 225
- [SD-008]
- [18]
Ann. Phys., 322 (2007), p. 667
- [SD-008]
- [19]
Physica A, 387 (2008), p. 3480
- [SD-008]
- [20]
Physica A, 394 (2014), p. 110
- [SD-008]
- [21]
Icarus, 277 (2016), p. 73
- [SD-008]
- [22]
Physica A, 391 (2012), p. 1546
- [SD-008]
- [23]
Planet. Space Sci., 70 (2012), p. 73
- [SD-008]
- [24]
Icarus, 264 (2016), p. 311
- [SD-008]
- [25]
Physica A, 388 (2009), p. 491
- [SD-008]
- [26]
Physica A, 388 (2009), p. 483
- [SD-008]
- [27]
Physica A, 392 (2013), p. 485
- [SD-008]
- [28]
Physica A, 415 (2014), p. 172
- [SD-008]
- [29]
Physica A, 452 (2016), p. 311
- [SD-008]
- [30]
Physica A, 461 (2016), p. 299
- [SD-008]
- [31]
Physica A, 462 (2016), p. 508
- [SD-008]
- [32]
Physica A, 389 (2010), p. 5581
- [SD-008]
- [33]
Physica A, 391 (2012), p. 6121
- [SD-008]
- [34]
Phys. Rev. E, 71 (2005), p. 046128
- [SD-008]
- [35]
Physica A, 387 (2008), p. 3201
- [SD-008]
- [36]
Entropy 17 (2015), p. 1103
- [SD-008]
- [37]
Phys. Rev. E, 89 (2014), p. 052142
- [SD-008]
- [38]
Physica A, 427 (2015), p. 1
- [SD-008]
- [39]
Astropart. Phys., 84 (2016), p. 36
- [SD-008]
- [40]
Physica A, 451 (2016), p. 456
- [SD-008]
- [41]
Europhys. Lett., 106 (2014), p. 39001
- [SD-008]
- [42]
Phys. Lett. A, 378 (2014), p. 2337
- [SD-008]
- [43]
Phys. Lett. A, 378 (2014), p. 2915
- [SD-008]
- [44]
Physica B, 405 (2010), p. 1022
- [SD-008]
- [45]
Astrophys. J., 413 (1993), p. 281
- [SD-008]
- [46]
Astrophys. J. Suppl., 126 (2000), p. 19
- [SD-008]
- [47]
Physica A, 385 (2007), p. 558
- [SD-008]
- [48]
Phys. Lett. A, 372 (2008), p. 4344
- [SD-008]
- [49]
Phys. Lett. A, 377 (2013), p. 3247
- [SD-008]
- [50]
Europhys. Lett., 104 (2013), p. 19001
- [SD-008]
- [51]
J. High Energy Astrophys., 8 (2015), p. 10
- [SD-008]
- [52]
Astropart. Phys., 39 (2012), p. 129
- [SD-008]
- [53]
Astropart. Phys., 39 (2012), p. 52
- [SD-008]

.png)